The structures hitherto considered in the present chapter have been of the type in which the members have been subjected to axial loads of tension or compression. Another very common type of structural member is a beam, which is defined as a member whose loads are primarily transverse to its axis rather than in the direction of the axis. These transverse loads cause a bending of the beam, instead of the extensions and compressions associated with the axial loads. The forces which are exerted on the beam by its supports are called the beam reactions, to distinguish them from the active forces which form the useful load on the beam. The computation of these reaction forces is the first step in the design of any beam.

The type of reactive force system set up will depend upon the way in which the beam is supported. We shall limit our present discussion to statically determinate supports, so that the reaction forces will in all cases be determined completely from the equations of statics applied to the whole beam as a free body.

The two most common types of beams are the simply supported beam on two supports and the cantilever beam, as shown in Fig. 1.

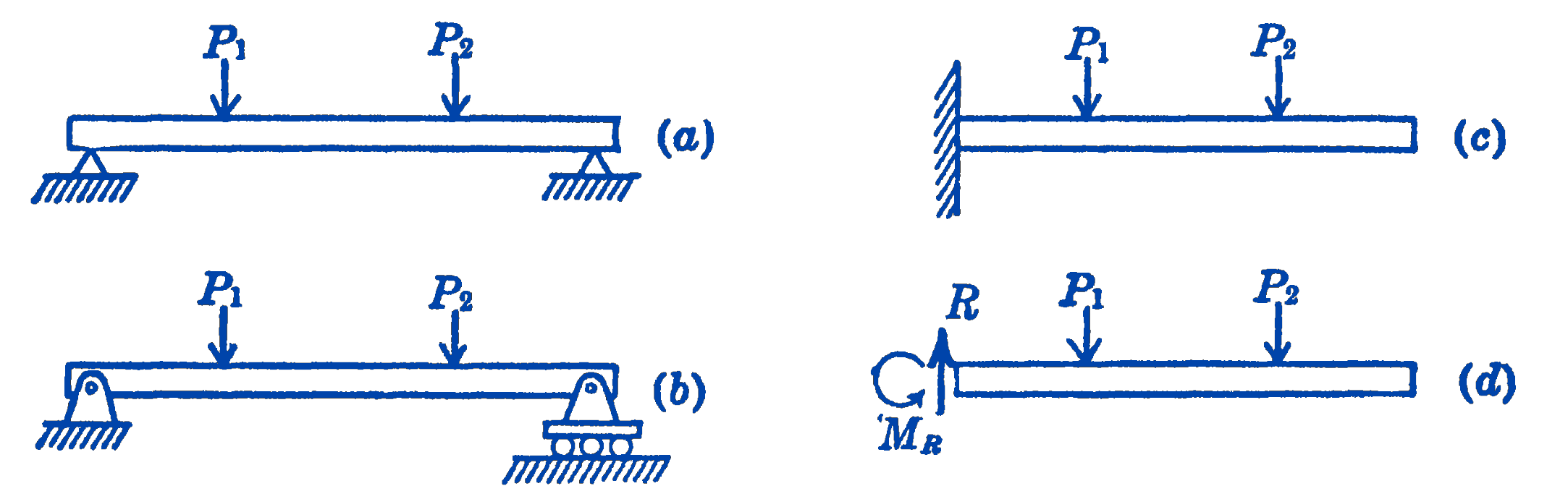
Considering only loads normal to the beam axis, the simply supported beam of Fig. 1a is supported in such a way that the reactive forces are normal to the beam. If one end of the beam is pinned, for example, the other end must be supported on frictionless rollers, as in Fig. 1b, so that no reactive force parallel to the beam can be developed. The cantilever beam of Fig. 1c is built in at one end in such a way that the direction of the tangent to the beam at that point is fixed. This requires that the support exert a moment on the beam, as is indicated in Fig. 1d.