Suppose that the moment of inertia of an area is known about one line, and that the moment of inertia of the same area about some other line, parallel to the first line, is to be determined.

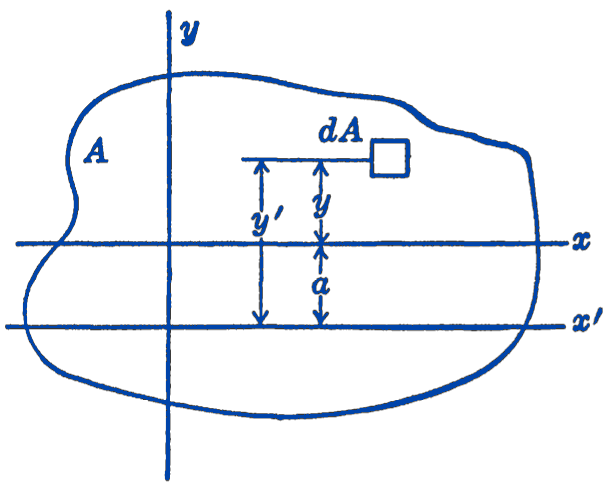
In Fig. 1 the known moment of inertia about the line \(x\) is \(I_{x}=\displaystyle \int y^{2}\, d A\) and the moment of inertia \(\displaystyle I_{x^{\prime}}=\int y^{\prime 2}\, d A\) is to be determined. The constant distance between the two parallel lines is \(a\). By definition: \[ \begin{aligned} I_{x^{\prime}}=\int y^{\prime 2}\, d A&=\int(y+a)^{2}\, d A\\ &=\int y^{2}\,d A+2 a \int y\,d A+a^{2} \int d A. \end{aligned} \] The first term \(\displaystyle \int y^{2}\, d A\) is \(I_{x}\), and the last term \(\displaystyle a^{2} \int d A\) is \(a^{2} A\). If we take the line \(x\) as passing through the centroid of the area, then the second term \(\displaystyle 2 a \int y\, dA=0\), and we have: \[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{I_{x^{\prime}}=I_{x_c}+a^{2} A,} \] where by the notation \(I_{x_c}\) we indicate that the \(x\)-axis passes through the centroid of the area. This expression, which is called the transfer theorem for moments of inertia, states that the moment of inertia of any area is equal to the sum of the moment of inertia of the area about a parallel centroidal axis and a term equal to the area multiplied by the square of the distance to the centroidal axis. It should be particularly noticed that the parallel axis must be a centroidal axis, otherwise the second term in the above analysis does not drop out, and the resulting expression has a more complex form. If the moment of inertia is known about some non-centroidal axis, and it is desired to find the moment of inertia about some other parallel non-centroidal axis, the parallel axis theorem must first be used to find the moment of inertia through the centroidal axis as an intermediate step in the problem.

Centroid locations and moments of inertia for a number of commonly encountered figures are given in Appendix.