Consider an element of a fluid in the form of a vertical cylinder, located as shown in Fig. 1.

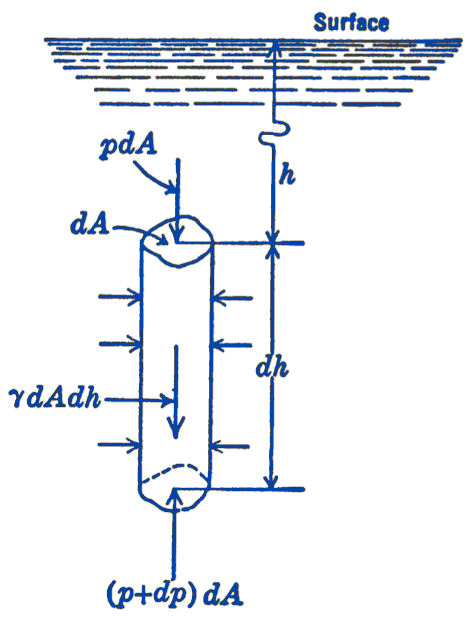
If we draw a free-body diagram of this element in equilibrium, we will have acting the forces shown; a force \(p\,d A\) acting vertically downward on the top of the element, an upward force \((p+d p) d A\) acting on the bottom of the element, and a gravity force equal to the weight of the fluid in the element. Using the notation:

\(\rho=\) the density of the fluid \(=\) the mass per unit volume \(\gamma=\rho g=\) the specific weight of the fluid \(=\) the weight per unit volume, where \(g\) is the acceleration of gravity

the weight of the fluid in the element is: \[ \gamma\, dA\,dh. \] For equilibrium, we have: \[ \begin{gathered} \sum F_{y}=0=(p+d p)\,d A-p\,d A-\gamma\, d A\, d h \\ d p-\gamma\,d h=0 \\ \frac{d p}{d h}=\gamma \end{gathered} \] From this relationship we can determine the variation of pressure with depth in an incompressible fluid, for which \(\gamma\) is a constant: \[ \begin{aligned} \int_{p_{1}}^{p_{1}} d p & =\gamma \int_{n_{1}}^{h_{2}} d h \\ \left(p_{2}-p_{1}\right) & =\gamma\left(h_{2}-h_{1}\right) \end{aligned} \] hence the difference in pressure at two points varies directly with the difference in the depth of the two points.