Consider a very small volume of fluid in the form of a triangular prism, as shown in Fig. 1.

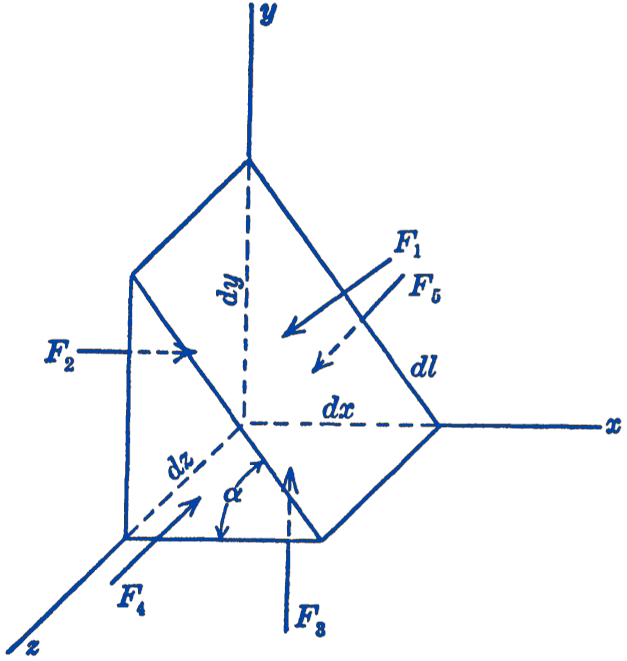
From the definition of a fluid we know that under equilibrium conditions the forces \(F_{1}, F_{2}\), etc., exerted on the faces of the prism by the fluid, are normal to the surfaces, i.e., there are no tangential forces in a fluid at rest. We define the pressure in the fluid as the surface force per unit area, and we shall denote such pressures by the small letter \(p\). Hence in Fig. 1 the pressure \(p_{1}\), associated with the force \(F_{1}\) would be \(\dfrac{F_{1}}{dz\, dl}\), assuming that the surfaces of the element are sufficiently small so that the force may be said to be uniformly distributed over the faces of the element.

Summing up the forces in the \(x\) and \(y\) directions, we have for the equilibrium condition: \[ \begin{aligned} & \sum F_{x}=0=p_{2}\,d y\, d z-p_{1}\,d z\,d l\, \sin \alpha, \\ & \sum F_{y}=0=p_{3}\,d x\, d z-p_{1}\,d z\,d l\, \cos \alpha. \end{aligned} \] In these equations we neglect any body forces proportional to the volume of the element, such as gravity forces, since as the element becomes infinitely small such body forces would involve small quantities of the third order, whereas the surface forces involve terms of the second order.

From the above equations, noting that \(d l \sin \alpha=d y\) and \(d l \cos \alpha=d x\), we have: \[ \begin{gathered} p_{2}\ d y d z-p_{1}\ d y d z=0, \\ p_{3}\ d x d z-p_{1}\ d x d z=0. \end{gathered} \] Therefore, \[p_{1}=p_{2}=p_{3}.\]

Since we have taken \(\alpha\) as any angle, we can conclude that the pressure at a point in a fluid is the same on any surface passing through that point, independent of the direction of that surface. This is one of the fundamental differences between an ideal fluid and such bodies as an elastic solid, in which the pressure does depend upon the direction of the surface on which it acts.