It is also convenient to define a moment of inertia of an area about a line normal to the plane of the area. In Fig. 1 the \(x y\) axes are in the plane of the area; \(r\) is the distance from the \(z\)-axis to an element of area \(d A\). The polar moment of inertia of the area is then defined as: \[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{J_O=\int r^{2} d A} \]
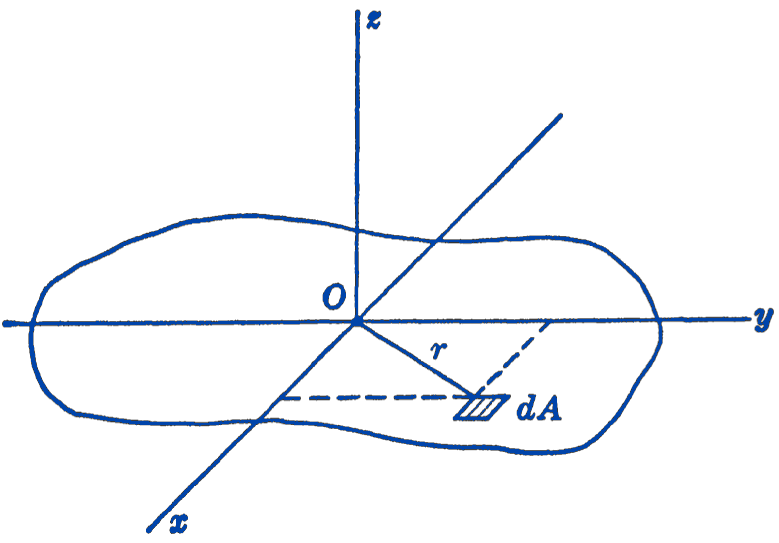
We may also write \(r^{2}=x^{2}+y^{2}\), so that: \[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{J_O=\int x^{2} d A+\int y^{2} d A=I_{y}+I_{x}} \] Therefore the polar moment of inertia of an area about an axis through a point is equal to the sum of the moments of inertia of the area about two perpendicular axes in the area passing through the same point.
Example 1. Find the location of the centroid of the volume of a hemisphere of radius \(r\) (Fig. 2).
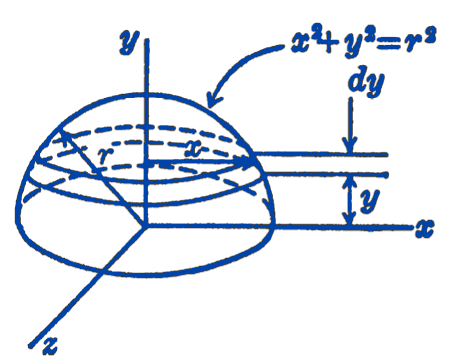
Solution. We know that the centroid lies somewhere on the axis of symmetry of the hemisphere. Taking the axis of symmetry as the \(y\)-axis, the centroid can be located completely by finding \(y_{c}\). Taking elementary slices of the hemisphere parallel to the \(x z\) plane, we have: \[ \begin{aligned} y_{c} & =\frac{\displaystyle \int y d V}{\displaystyle\int d V}=\frac{\displaystyle\int_{0}^{r} y\left(\pi x^{2} d y\right)}{\displaystyle\int_{0}^{r} \pi x^{2} d y}=\frac{\displaystyle\int_{0}^{r} y\left(r^{2}-y^{2}\right) d y}{\displaystyle \int_{0}^{r}\left(r^{2}-y^{2}\right) d y} \\ & =\frac{\left.\left(\dfrac{r^{2} y^{2}}{2}-\dfrac{y^{4}}{4}\right)\right|_{0} ^{r}}{\left.\left(r^{2} y-\dfrac{y^{3}}{3}\right)\right|_{0} ^{r}}=\frac{\left(\dfrac{1}{2}-\dfrac{1}{4}\right)}{\left(1-\dfrac{1}{3}\right)} r\\ &=\frac{3}{8} r \end{aligned} \]
Example 2. Find the moment of inertia of the area of a triangle about a line parallel to a base passing through the centroid of the area (Fig. 3).
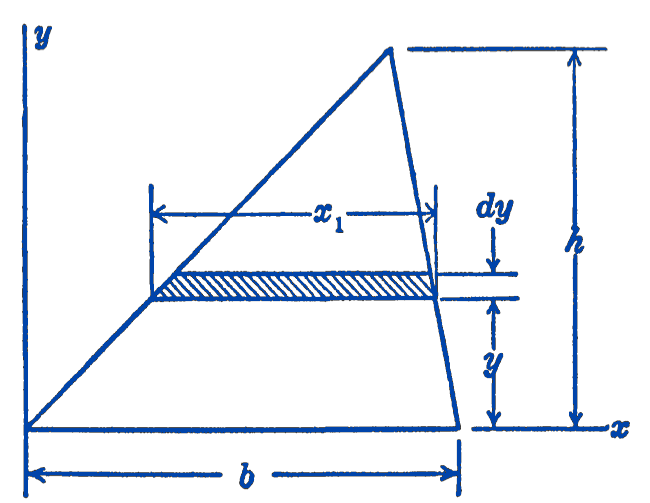
Solution. We shall first find by direct integration the moment of inertia of the area of the triangle about the base. \[ \begin{aligned} I_{x} & =\int y^{2}\, d A=\int_{0}^{h} y^{2} x_{1}\, d y \\ & =\frac{b}{h} \int_{0}^{h}(h-y) y^{2}\, d y \\ & =\left.\frac{b}{h}\left(\frac{h y^{3}}{3}-\frac{y^{4}}{4}\right)\right|_{0} ^{h}=\frac{1}{12} b h^{3} \end{aligned} \] Now, using the transfer theorem for parallel axes, we have: \[ \begin{aligned} & I_{x}=I_{xc}+\left(\frac{h}{3}\right)^{2}\left(\frac{1}{2} b h\right) \\ & I_{xc}=\frac{1}{12} b h^{3}-\frac{1}{18} b h^{3}=\frac{1}{36} b h^{3} \end{aligned} \]
Example 3. Find the centroid of the area shown in Fig. 4.
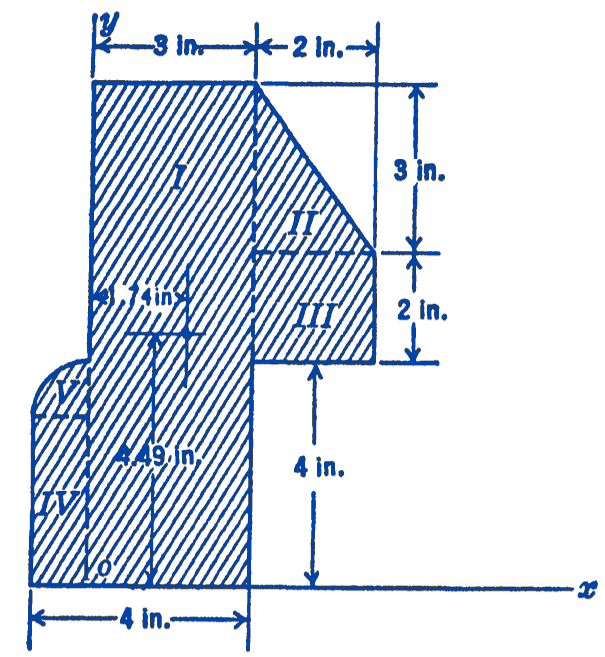
Solution. We first divide the figure into a number of simpler figures, each of which has a known centroidal distance. In the present case we have enough pieces so that it will be desirable to systematize the calculations by placing them in a tabular form. Such tabular forms have a number of advantages. They are very easy to check because one knows at a glance just what the significance of each number on the sheet is, and the organization of complicated calculations in a tabulation form makes it possible to employ relatively unskilled computers for routine calculations.
| Part | Area \(A\) \((\mathrm{in}^{2})\) | Centroidal Dist. \(x\ (\mathrm{in})\) | Centroidal Dist. \(y\ (\mathrm{in})\) | \((A)(x)\) ( \(\mathrm{in}^{3}\)) | \((A)(y)\) ( \(\mathrm{in}^{3}\)) |
|---|---|---|---|---|---|
| I | \(27\) | \(\frac{1}{2}\cdot 3=1.5\) | \(\frac{1}{2}\cdot 9=4.5\) | \(40.5\) | \(121.5\) |
| II | \(3\) | \(3+\frac{1}{3}\cdot 2 =3.67\) | \(6+\frac{1}{3}\cdot 3=7\) | \(11.0\) | \(21.0\) |
| III | \(4\) | \(3+\frac{1}{2}\cdot 2=4\) | \(4+\frac{1}{2}\cdot 2=5\) | \(16.0\) | \(20.0\) |
| IV | \(3\) | \(\frac{1}{2}(-1)=-0.5\) | \(\frac{1}{2}\cdot 3=1.5\) | \(-1.5\) | \(4.5\) |
| V | \(\frac{\pi}{4}=0.79\) | \(-\frac{4\times 1}{3\pi}=-0.42\) | \(3+\frac{4\times 1}{3\pi}=3.42\) | \(-0.3\) | \(2.7\) |
| \(\sum\) | \(37.8\) | \(65.7\) | \(169.7\) |
\[ x_{c}=\frac{65.7}{37.8}=1.74 ; \quad y_{c}=\frac{169.7}{37.8}=4.49 \]
Example 4. Find the moment of inertia of the area shown in Example 3 about the \(x\)-axis.
Solution. The area is subdivided into the same elements as were used in the preceding problem. For each of these elements the moment of inertia about an axis through the centroid of the element parallel to the \(x\)-axis can be computed, by looking up the formula for the moment of inertia of the element in the appendix. The transfer theorem can then be used to find the moment of inertia of each element about the \(x\)-axis, and the sum of these values will be the moment of inertia of the whole area. These calculations may be conveniently arranged in tabular form:
| Part | \(I_{c}\) \((\mathrm{in})\) | \(y_{c}\) \((\mathrm{in})\) | \(y_{c}{ }^{2}\) \((\mathrm{in}^2)\) | \(A\) \((\mathrm{in}^2)\) | \(A y_{c}{ }^{2}\) \((\mathrm{in}^4)\) | \(I_{x}=I_{c}+A y_{c}{ }^{2}\) \((\mathrm{in}^4)\) |
|---|---|---|---|---|---|---|
| I | 182.2 | 4.5 | 20.3 | 27 | 548 | 730 |
| II | 1.5 | 7 | 49 | 3 | 147 | 149 |
| III | 1.33 | 5 | 25 | 4 | 100 | 101 |
| IV | 2.25 | 1.5 | 2.25 | 3 | 6.75 | 9 |
| V | 0.055 | 3.42 | 11.7 | 0.79 | 9.24 | 9 |
| \(\sum\) | 998 |
4.6.1 PROBLEMS
1. (a) Show that the area of the surface generated by rotating any plane curve about a non-intersecting axis in the plane of the curve is equal to the length of the curve times the distance traveled by the centroid of the curve.*
- Show that the volume of the solid generated by rotating any plane figure about a non-intersecting axis in the plane of the figure is equal to the area of the figure times the distance traveled by the centroid of the area.1
2. Find the center of gravity of a fine wire bent in the shape of a quarter-circle. Using this result, find the surface area of a sphere.
3. Find the centroid of the area under one-half cycle of a sine wave.
4. Find the centroid of a segment of a circle of radius \(r\) subtended by the angle \(\alpha\).
5. Show that the centroid of the volume of any cone or pyramid is located a distance of three-fourths of the altitude from the apex.
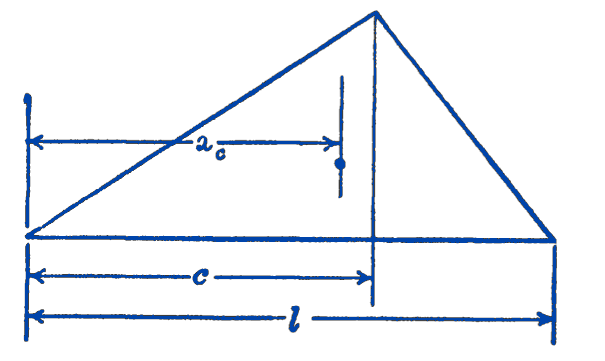
6. Show that for the triangle shown in the figure: \[ x_{c}=\frac{l+c}{3} \]
7. A glass is partially filled with water. Show that the center of gravity of the glass and the water is lowest when this center of gravity is located in the surface of the water.
8. Find the moment of inertia of the area of a circle with respect to a diameter of the circle.
9. Find the polar moment of inertia of the area of a rectangle with respect to an axis normal to the area passing through the centroid of the rectangle.
10. Show that the polar moment of inertia of an area about any axis is equal to the sum of the polar moment of inertia of the area about the centroidal axis and the product of the area and the square of the distance between the axes.
11. Find the moment of inertia of the shaded area shown in the diagram about the axis \(x x\).
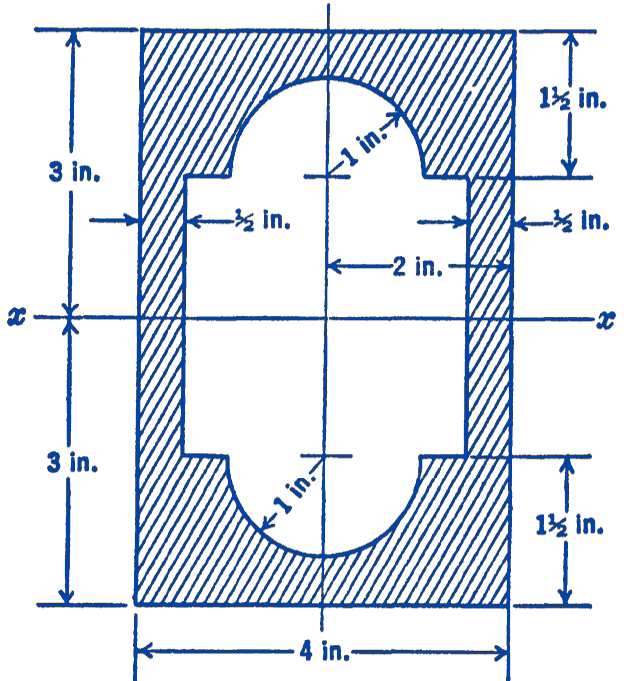
Answer
53.4 in\({ }^{4}\)
12. Find the centroid of the volume shown in the figure.
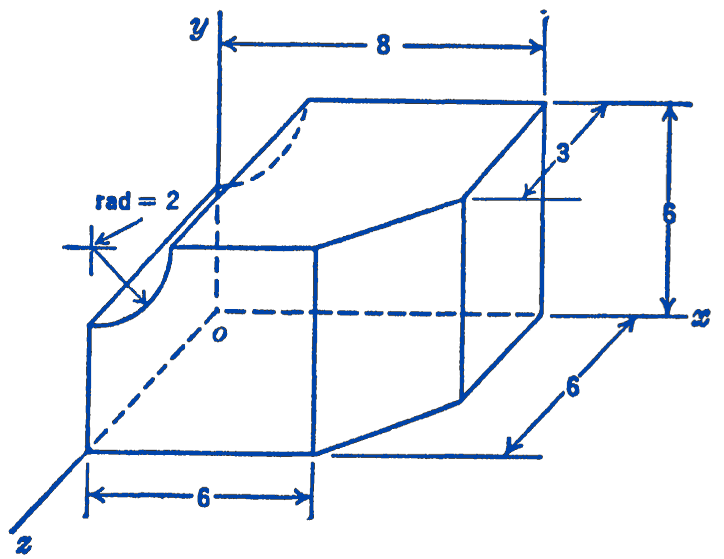
Answer
\(x_{c}=4.00, y_{c}=2.84, z_{c}=2.86\)
13. The cross section of a V-belt pulley has the dimensions shown in the figure. If the pulley is made of steel weighing \(0.283 \mathrm{lb}\) per cu in., find the weight of the pulley.
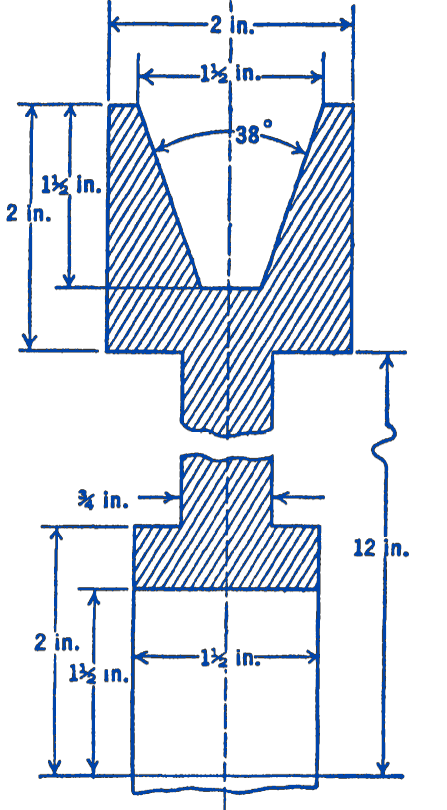
Answer
154 lb
14. Find the center of gravity of a homogeneous solid having the shape shown in the figure.
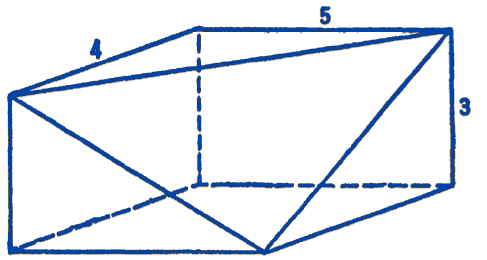
Answer
\(x_{c}=2.25, y_{c}=1.35, z_{c}=1.80\)
15. A 3-in. diameter hole is drilled into a cone as shown below in the figure. What should be the depth \(h\) of the hole if the centroid of the remaining volume is to be located a distance \(h\) from the base of the cone?
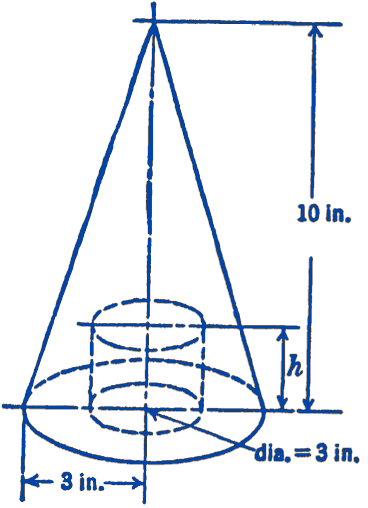
Answer
\(h=2.8\) in.
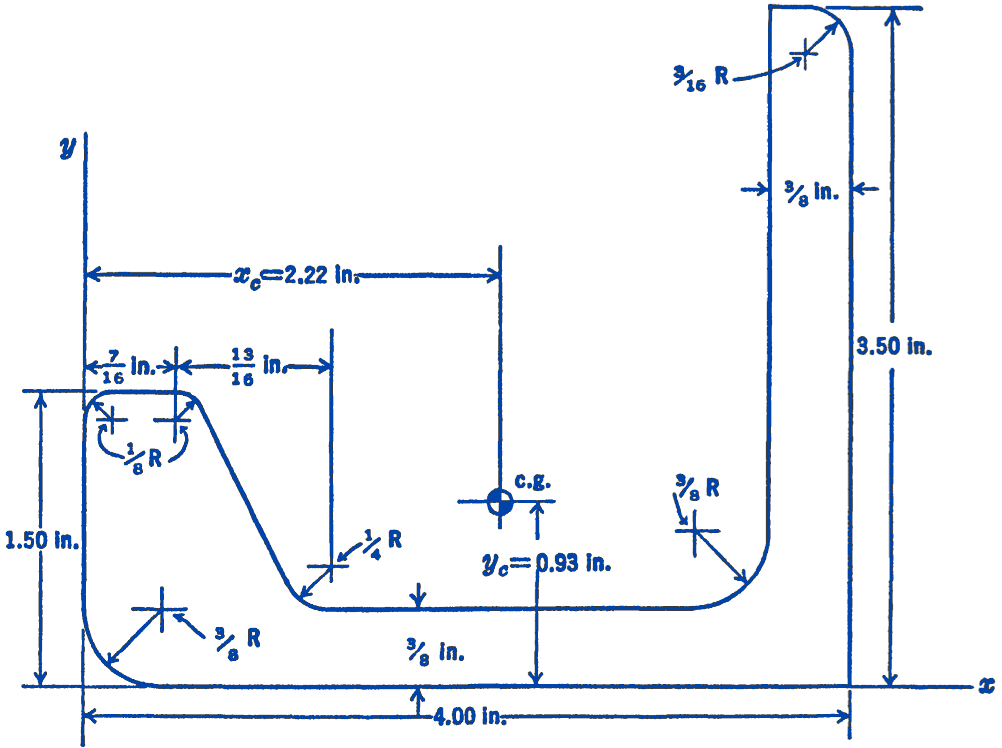
16. One standard size of the structural shape known as a bulb angle has the dimensions shown in the figure:
- The Structural Aluminum Handbook gives the following location for the center of gravity of the area: \(x_{c}=2.22\ \mathrm{in}\).; and \(y_{c}=0.93\ \mathrm{in}\). Check these values, neglecting the small areas represented by the fillets and rounded corners.
- The Structural Aluminum Handbook gives the moment of inertia of the area about the \(x_{c}\)-axis as \(3.02\ \mathrm{in}^4\). Check this value.
- These “theorems” are due to Pappus (A.D. 300), and were later independently noted by Guldinus (1635-1642).↩︎