When determining the moment of inertia of an area by integration it will usually be found that while it may be relatively easy to perform the integrations for certain positions of the axis, other positions may be difficult because of the shape of the boundary of the area. For example, the moment of inertia of a rectangular area may easily be found by integration for any axis which is parallel to one of the sides. For an axis which is inclined at an angle to the sides, however, the integration and the substitution of the boundary conditions become more difficult. We should like, therefore, a method of determining the moment of inertia of an area about any inclined axis in an area, given the moment of inertia about some other axis.
In Fig. 1 suppose that the moments of inertia \(I_{x}\) and \(I_{\nu}\) about the \(x y\) axes are known, and that it is desired to find the moment of inertia \(I_{x^{\prime}}\) about the \(x^{\prime}\)-axis which makes an angle \(\phi\) with the \(x\)-axis.
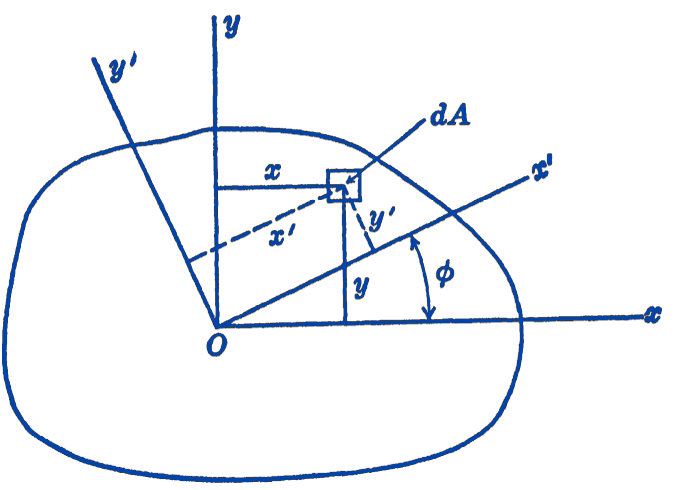
The coordinates of an element of area \(d A\) in the \(x^{\prime} y^{\prime}\) system can be expressed in terms of the coordinates in the \(x y\) system. \[ \begin{aligned} & x^{\prime}=x \cos \phi+y \sin \phi \\ & y^{\prime}=y \cos \phi-x \sin \phi \end{aligned} \] The moment of inertia about the \(x^{\prime}\)-axis is then given by: \[ \begin{aligned} I_{x^{\prime}} & =\int_{A} y^{\prime 2}\, d A=\int_{A}(y \cos \phi-x \sin \phi)^{2}\, d A \\ & =\int_{A} y^{2} \cos ^{2} \phi\,d A-\int_{A} 2 x y \sin \phi \cos \phi\,d A+\int_{A} x^{2} \sin ^{2} \phi\, d A \\ & =I_{x} \cos ^{2} \phi+I_{y} \sin ^{2} \phi-I_{x y} \sin 2 \phi \end{aligned} \] Putting \(\cos ^{2} \phi=\frac{1}{2}(1+\cos 2 \phi)\) and \(\sin ^{2} \phi=\frac{1}{2}(1-\cos 2 \phi)\), this expression becomes: \[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{I_{x^{\prime}}=\frac{I_x+I_{y}}{2}+\frac{I_{x}-I_{y}}{2} \cos 2 \phi-I_{x y} \sin 2 \phi} \] Thus if the moments of inertia \(I_{x}\) and \(I_{y}\), and the product of inertia \(I_{x y}\) are known, the moment of inertia about any inclined axis may be found.
Example. Find the moment of inertia of the area of a rectangle about one of the long diagonals (Fig. 2).
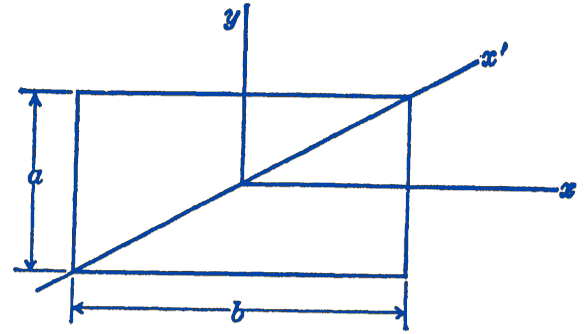
Solution. We shall take the center of the rectangle as the origin of an \(x y\) coordinate system. In this system, we have: \[ \begin{aligned} I_{x} & =\frac{b a^{3}}{12} \\ I_{y} & =\frac{a b^{3}}{12} \\ I_{x y} & =0 \end{aligned} \] The general expression for the moment of inertia about an inclined axis \(x^{\prime}\) is: \[ I_{x^{\prime}}=\frac{I_{x}+I_{y}}{2}+\frac{I_{x}-I_{y}}{2} \cos 2 \phi-I_{x y} \sin 2 \phi \] In this case: \[ \begin{aligned} \cos 2 \phi&=1-2 \sin ^{2} \phi\\ &=1-2\left(\frac{a^{2}}{a^{2}+b^{2}}\right)\\ &=\frac{b^{2}-a^{2}}{a^{2}+b^{2}} \end{aligned} \] So that: \[ I_{x^{\prime}}=\frac{a^{3} b^{3}}{6\left(a^{2}+b^{2}\right)} \]
4.8.1 PROBLEMS
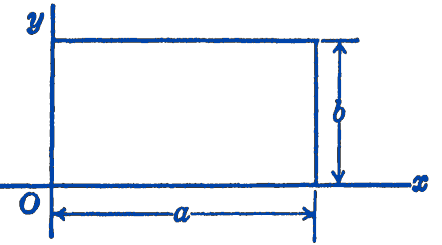
1. Find by integration the product of inertia \(I_{x y}\) of the area of a rectangle which lies in the first quadrant as shown in the figure. Check this result by using the transfer theorem for products of inertia.
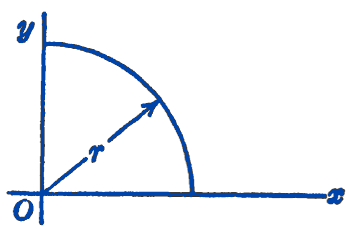
2. Find the product of inertia \(I_{x y}\) of the area of a quarter circle, oriented as shown in the figure.
3. Find the product of inertia \(I_{x y}\) of the figure shown in Example 3 of Section: The Polar Moment of Inertia of an Area.
4. Show that the sum of the moments of inertia about two perpendicular axes in the plane of an area is a constant independent of the angle of rotation of the axes in the area, e.g., in Fig. 1, \(I_{x^{\prime}}+I_{y^{\prime}}=\) constant. Show that this result would be expected from the definition of the polar moment of inertia.

5. Show that the product of inertia of an area with respect to two inclined axes (as in the following figure) is given by: \[ I_{x^{\prime} y^{\prime}}=\frac{I_{x}-I_y}{2} \sin 2 \phi+I_{x y} \cos 2 \phi \]

6. Show that the angle defining the axis about which the moment of inertia is a maximum or a minimum is given by (see the figure of the previous problem): \[ \tan 2 \phi=\frac{2 I_{x y}}{I_{y}-I_{x}}. \] Show that if the moment of inertia is a maximum about one axis, then it is a minimum about the perpendicular axis. The axis about which the moments of inertia are maximum and minimum are called the principal axes of the area.
7. Show that the product of inertia of an area with respect to the principal axes is equal to zero (refer to Problem 108 above).
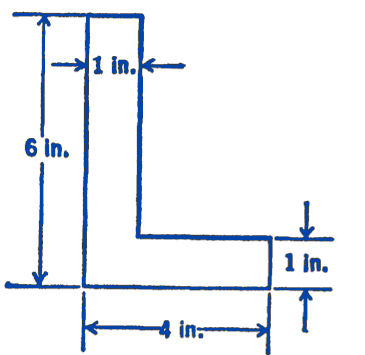
8. The Structural Steel Handbook states that the least radius of gyration of the cross-sectional area of a \(6 \times 4 \times 1\ \mathrm{in}\) thick angle-iron section about any line in the area is \(0.86\ \mathrm{in}\). How closely is this value checked by assuming that the shape of the section is as given in the diagram? The value of this least radius of gyration is required for an analysis of the strength of such a structural member.