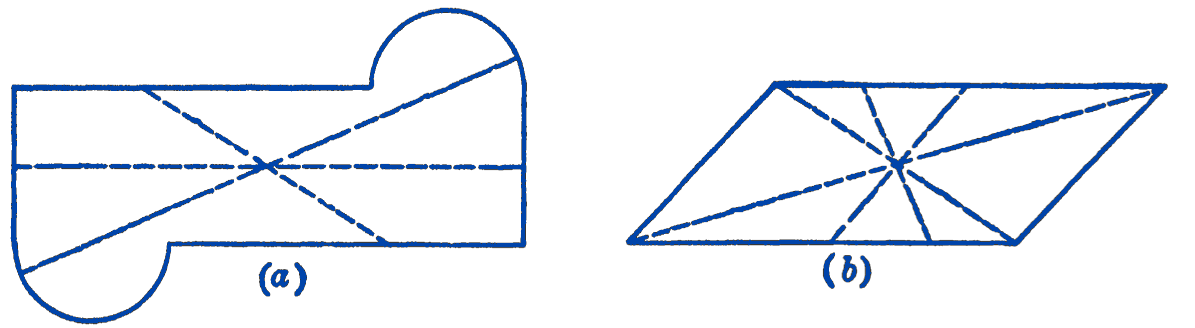
In many cases the location of the centroid or center of gravity of a figure can be found by a consideration of the symmetry of the shape. If an area has an axis of symmetry, the centroid must be somewhere on this axis, and, if the area has two axes of symmetry, the centroid lies at the intersection of the two axes. Some figures which do not have an axis of symmetry may be said to have a center of figure, i.e., a point which is the midpoint of all elements of the figure which pass through the point. This point in many cases can be determined by inspection, as in the examples shown in Fig. 1.

The location of the centroids of a number of simple shapes can be found directly from the defining equations. For more complicated figures, the most useful scheme is to subdivide the shape into simple elements, for each of which the centroidal distances are known or may be easily determined. By summing up the moments of the individual elements, the centroid of the whole figure is determined by the principle of moments. If it is not possible to subdivide the figure into simple figures for which the centroidal locations will be known, approximate solutions to any desired accuracy may be made by using sufficiently small elements.

The moments of inertia of many simple areas may be found directly by integration of the defining equations. For more complicated areas, the areas may be subdivided and the moments of inertias combined as discussed in the following paragraphs.