Consider a system of particles having masses \(m_{1}, m_{2}, \cdots\) as shown in Fig. 1, and let each particle be located by its radius vector \(\mathbf{r}\) from the origin of a rectangular coordinate system.

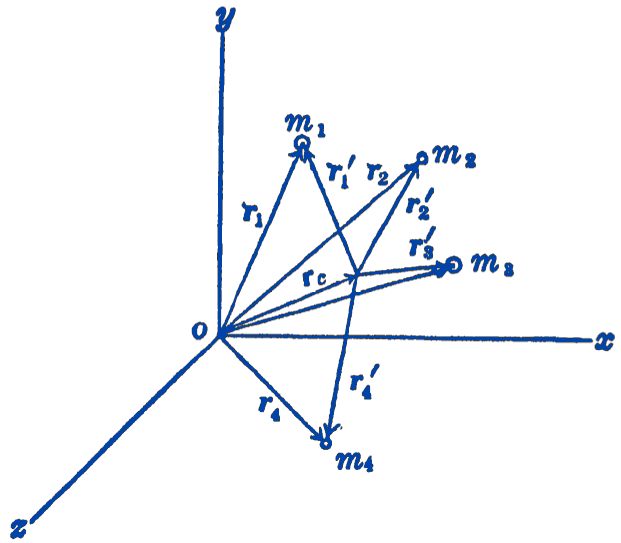
The center of mass of the system of particles is a point defined by the following expression: \[ \begin{equation*} \mathbf{r}_{c}=\frac{\displaystyle \sum m \mathbf{r}}{\displaystyle\sum m} \tag{1} \end{equation*} \]

We can show that this point has the property that, if we multiply each mass by the vector from the center of mass to the particle, the sum of these moment products is zero, for: \[ \begin{aligned} \sum m \mathbf{r}^{\prime} & =\sum m\left(\mathbf{r}-\mathbf{r}_{c}\right)=\sum m \mathbf{r}-\sum m \mathbf{r}_{c} \\ & =\mathbf{r}_{c} \sum m-\mathbf{r}_{c} \sum m=0 \end{aligned} \] If we write \(r_{c}\) and \(r\) in terms of the rectangular components of the system, we have: \[ \begin{aligned} \mathbf{r}_{c} & =x_{c} \mathbf{i}+y_{c} \mathbf{j}+z_{c} \mathbf{k} \\ \mathbf{r} & =x \mathbf{i}+y \mathbf{j}+z \mathbf{k} \end{aligned} \] Substituting in equation (1) and equating components, we have: \[ \begin{aligned} x_{c} & =\frac{\displaystyle \sum m x}{\displaystyle\sum m} \\ y_{c} & =\frac{\displaystyle\sum m y}{\displaystyle\sum m} \\ z_{c} & =\frac{\displaystyle\sum m z}{\displaystyle \sum m} \end{aligned} \]

Since the gravity force on the particle is proportional to the mass of the particle, it will be seen that the center of mass coincides with the center of gravity for all those cases in which the gravity forces can be assumed to form a parallel force system. Thus in engineering practice the terms center of gravity and center of mass are often used synonymously.