Let us find the total force due to fluid pressure upon a submerged plane area \(A\). We will assume that at the surface of the fluid the pressure is zero (neglecting atmospheric pressure) and we will measure the depth \(h\) vertically downward from this free surface.

From the last equation of the preceding section, putting \(p_{1}=0\) when \(h=0\) \[ p=\gamma h \] Considering first the horizontal plane shown in Fig. 1a, we see that the pressure has everywhere on this plane the same value \(\mathbf{\gamma}\), so that the total downward force acting on the plane is \(\gamma h A\), acting at the centroid of the area. In the case of the vertical area, however (Fig. 1b), the pressure varies along the depth of the area, and the system of forces acting upon the area becomes a system of non-uniform parallel forces. The resultant of this non-uniform system of parallel forces passes through the centroid of the pressure diagram, rather than through the centroid of the area. The point on the submerged body at which the resultant of the pressure force acts is called the center of pressure.

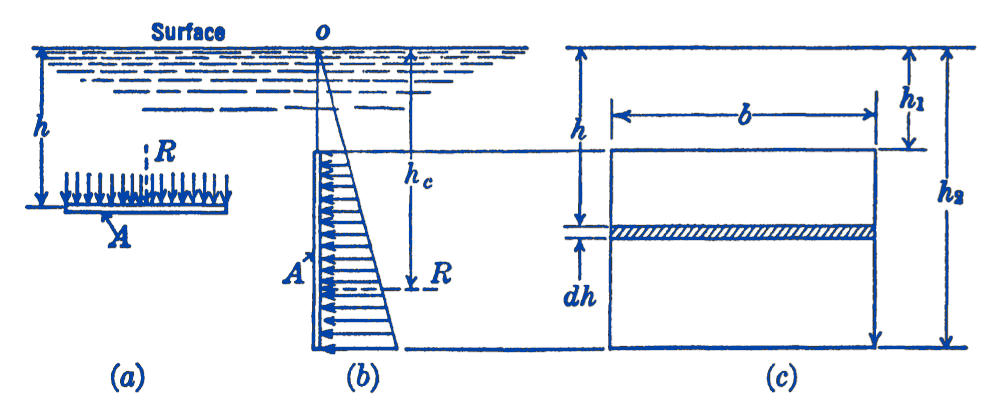
As an example, suppose we have a rectangular area, as shown in Fig. 1c. The total force on the area and the location of the center of pressure can be found by integration; the force on the shaded element of area is: \[ \gamma h b(d h) \] Summing up these forces we have for the total force \(R\) : \[ \begin{aligned} & R=\gamma b \int_{h_{1}}^{m_{2}} h\, d h=\left.\gamma b\left(\frac{h^{2}}{2}\right)\right|_{m_{1}} ^{m_{m}} \\ & R=\frac{\gamma b}{2}\left(h_{2}{ }^{2}-h_{1}{ }^{2}\right) \end{aligned} \] To find the center of pressure, take moments about the point \(O\) : \[ \begin{gathered} \left(h_{c}\right)(R)=\gamma b \int_{h_{1}}^{m_{1}} h^{2} d h=\left.\gamma b\left(\frac{h^{3}}{3}\right)\right|_{h_{1}} ^{n_{2}} \\ h_{c}=\frac{2}{3} \frac{\left(h_{2}{ }^{3}-h_{1}{ }^{3}\right)}{\left(h_{2}{ }^{2}-h_{1}{ }^{2}\right)} \\ \text { (for a rectangular area) } \end{gathered} \]