The previous considerations can be extended to include curved areas:

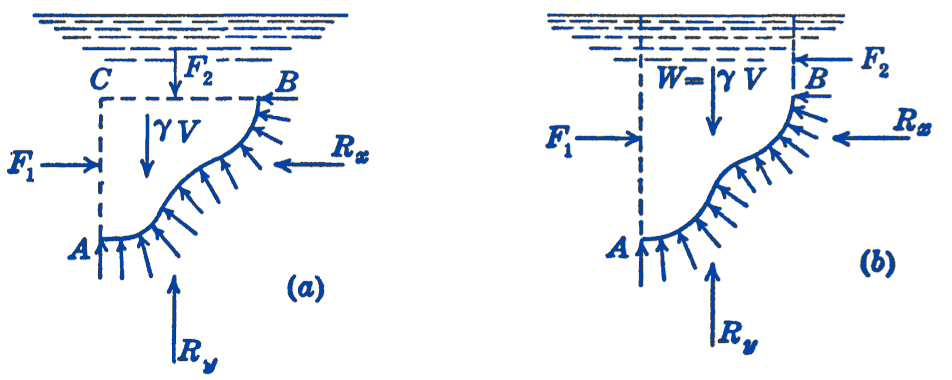
Let \(A B\) be the edge view of a cylindrical surface whose length perpendicular to the paper is unity. We wish to find the horizontal and vertical components \(R_{x}\) and \(R_{y}\) of the system of forces acting on one side of this surface due to the fluid.

In Fig. 1a imagine a fluid element bounded by \(A B\), a horizontal plane \(B C\), and three vertical planes. For equilibrium of this element, we have: \[ \begin{gathered} \sum F_{x}=0=F_{1}-R_{x} \\ R_{x}=F_{1} \end{gathered} \] Hence the magnitude and the location of the horizontal component will be the same as the force acting upon the vertical plane \(A C\) and can be computed as in the preceding section.

To find the vertical component, we imagine that the element extends to the free surface, as in Fig. 1b. The force on the top of this element will then be zero, and the condition for equilibrium is: \[ \begin{gathered} \sum F_{y}=0=R_{y}-\gamma V \\ R_{y}=W \end{gathered} \] Hence the vertical component of force is equal in magnitude to the weight of the fluid contained in the vertical column above the area, and passes through the center of gravity of that fluid element. It will be seen that this same result would be obtained for an area element of any kind.

If we apply the above principles to the case of a closed area, such as the surface of a submerged body, we are led directly to Archimedes’ Principle for a floating body.

Consider the forces acting upon a cylindrical element of a submerged body, as shown in Fig. 2.

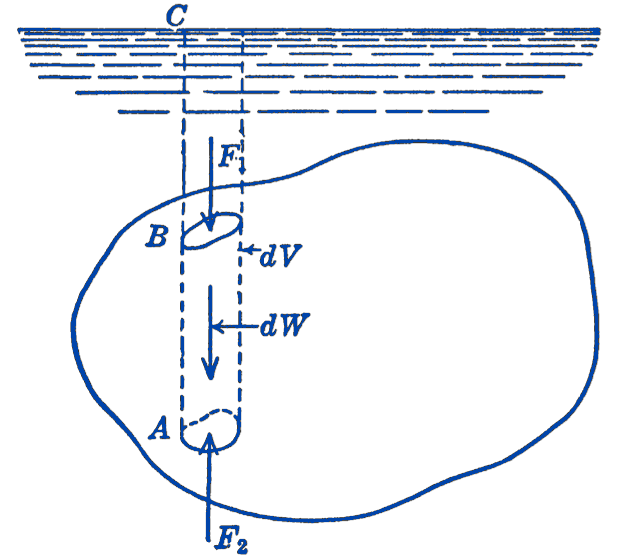
Considering the area at \(A\), there will be acting at \(A\) a force \(F_{2}\) which is equal to the weight of the fluid in the column \(A C\). There is also acting at \(B\) a downward force \(F_{1}\), which is equal to the weight of the fluid in the column \(B C\). There will thus be a net upward force \(F_{2}-F_{1}\) acting on the element which will be equal to the weight of the fluid contained in the volume \(d V\), i.e., the volume of the column \(A B\). This net upward force upon the element is called a buoyant force. If we now add up the buoyant forces on all of the elements of the body, we find that the total buoyant force acting upon the body is equal to the weight of the fluid displaced by the body.