By generalizing the concept of a moment, the above ideas can be extended to several other important problems.

Suppose that we have given an infinitesimal area, \(d A\), located at a distance \(x\) from some axis. We then say that the moment of the area about the axis is the product \(x\, d A\). To find the moment of any finite plane area about any line in its plane we have only to add up the moments of all of the elements, as shown in Fig. 1.

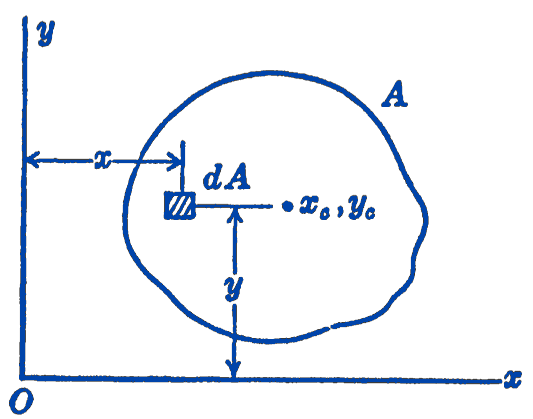
The moment of \(d A\) about the \(y\)-axis is \(x\, d A\), and the total moment of the whole area about the \(y\)-axis is ¹: \[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{Q_{y}=\int x\, d A} \]

We now define the distance \(x_{c}\) such that this distance multiplied by the total area will equal the moment of the area about the \(y\)-axis: \[ \left(x_{c}\right)(A)=\int x d A \] In a similar way, the distance \(y_{c}\) is defined \[ \left(y_{c}\right)(A)=\int y d A \] The point located by the coordinates \(x_{c}, y_{c}\) \[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{\begin{aligned} & x_{c}=\frac{\displaystyle\int x\, d A}{\displaystyle\int d A} \\ \\ & y_{c}=\frac{\displaystyle\int y\, d A}{\displaystyle\int d A} \end{aligned}} \] is called the centroid of the area.

The quantity \(\displaystyle \int x\, d A\) which we have called the moment of the area is often called the first moment of the area, and the expression \(\displaystyle \int x^{2}\, d A\) is called the second moment. The name moment of inertia of the area is commonly used instead of the name second moment. A length \(r\) can be determined so that: \[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{r^{2}=\frac{\displaystyle \int x^{2} d A}{A}} \] This distance \(r\) is called the radius of gyration of the area about the \(y\)-axis.

These concepts of the moments of an area and of the centroidal distance and the radius of gyration will be found later to be useful in the analysis of a number of problems in the fields of dynamics and theory of elasticity.

The centroid of a length, a non-coplanar area, or a volume may be defined in the same way as we have defined the centroid of a plane area. Writing down the rectangular components of these centroids we have:

For the line of length \(l\) : \[ x_{c}=\frac{\displaystyle \int x\,dl}{\displaystyle\int d l} ; \quad y_{c}=\frac{\displaystyle\int y\,d l}{\displaystyle\int d l} ; \quad z_{c}=\frac{\displaystyle\int z\,dl}{\displaystyle\int d l} \] For the surface area \(S\): \[ x_{c}=\frac{\displaystyle\int x\,d S}{\displaystyle\int d S} ; \quad y_{c}=\frac{\displaystyle\int y\,d S}{\displaystyle\int d S} ; \quad z_{c}=\frac{\displaystyle\int z\,d S}{\displaystyle\int d S} \] For the volume \(V\): \[ x_{c}=\frac{\displaystyle\int x\,d V}{\displaystyle\int d V} ; \quad y_{c}=\frac{\displaystyle\int y\,d V}{\displaystyle\int d V} ; \quad z_{c}=\frac{\displaystyle\int z\,d V}{\displaystyle\int d V} \]

It will be seen that there is a close relationship between centroids and centers of gravity. The center of gravity of a homogeneous solid is located at the centroid of the volume of the solid. The terms centroid and center of gravity are used interchangeably in many books, although it is well to note that there are some cases, for example bodies with non-uniform specific weight distributions, in which the center of gravity might not coincide with the centroid of the volume.