To as good an approximation as is required in most engineering work, the system of gravity forces acting upon a body may be considered as a parallel force system. Since gravity forces are always present and must in most problems be taken into account, it will be desirable to simplify the treatment of such parallel force systems by means of a general analysis.

We shall first show that the system of parallel gravity forces acting upon a body has a resultant which passes through one particular point in the body, for any orientation of the body. This center of parallel gravity forces is called the center of gravity of the body, and the entire weight of the body can be considered as concentrated at that point, so far as statical considerations are concerned.

Consider a rigid system which is represented by the three particles of Fig. 1.

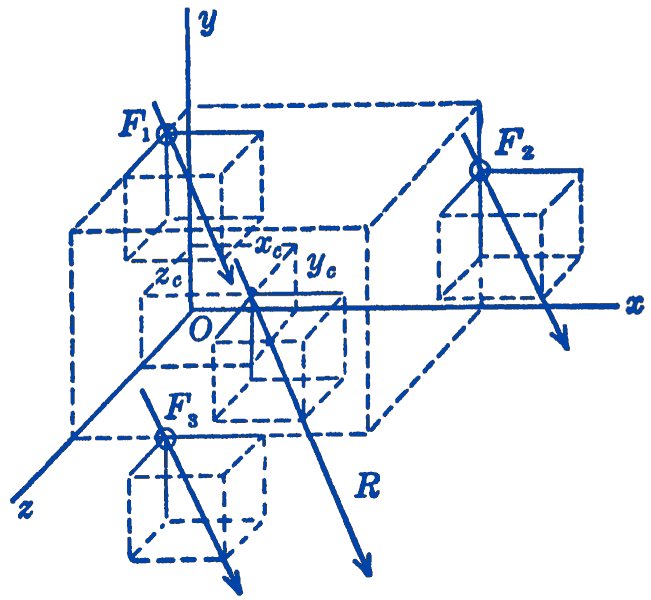
The system is acted upon by parallel gravity forces \(F_{1}, F_{2}\), and \(F_{3}\). In this figure, the \(y\)-axis is not the vertical direction, but the system has been given some general orientation in space.

We now resolve each of the parallel forces into the three rectangular components: \[ \begin{aligned} & F_{x}=k_{1} F \\ & F_{y}=k_{2} F \\ & F_{z}=k_{3} F \end{aligned} \] where \(k_{1}, k_{2}, k_{3}\) are the direction cosines and are the same for all of the forces, since the forces are parallel.

Considering the system of forces parallel to the \(x\)-axis, we have by the principle of moments: \[ \begin{aligned} & \left(R_{x}\right) y_{c}=\sum M_{z}=k_{1} F_{1} y_{1}+k_{1} F_{2} y_{2}+k_{1} F_{3} y_{3} \\ & \left(R_{y}\right) z_{c}=\sum M_{x}=k_{2} F_{1} z_{1}+k_{2} F_{2} z_{2}+k_{2} F_{3} z_{3} \end{aligned} \] but \[ R_{x}=k_{1} F_{1}+k_{1} F_{2}+k_{1} F_{3} \] so

\[ y_{c}=\frac{\displaystyle k_{1} \sum(F)(y)}{\displaystyle k_{1} \sum F}=\frac{\displaystyle\sum(F)(y)}{\displaystyle\sum F} \] and \[ z_{c}=\frac{\displaystyle\sum(F)(z)}{\displaystyle\sum F} \] Similarly, taking force components parallel to the \(y\)-axis, we find: \[ x_{c}=\frac{\displaystyle\sum(F)(x)}{\displaystyle\sum F} \]

We have thus defined a point \(x_{c}, y_{c}, z_{c}\), which is the point of application of the resultant of any parallel system of gravity forces. Since the particular direction cosines defining the orientation of the system cancel out of the analysis, it will be seen that the location of this center of parallel forces is independent of the orientation of the body. This point is called the center of gravity of the system.

Applying this principle to a homogeneous body of total weight \(W\), we can reduce this single force \(W\) to a system of parallel forces each of magnitude \(d W\) so that \(W=\displaystyle\int d W\). Then, if we locate each element of weight \(d W\) by the coordinates \(x, y, z\), we have for the location of the center of gravity of the body:

\[ \begin{aligned} & x_{c}=\frac{\displaystyle\int x\, d W}{\displaystyle\int d W} \\ \\ & y_{c}=\frac{\displaystyle\int y\, d W}{\displaystyle\int d W} \\ \\ & z_{c}=\frac{\displaystyle\int z\, dW}{\displaystyle\int d W} \end{aligned} \]