Consider an imaginary surface that cuts a body into two parts.

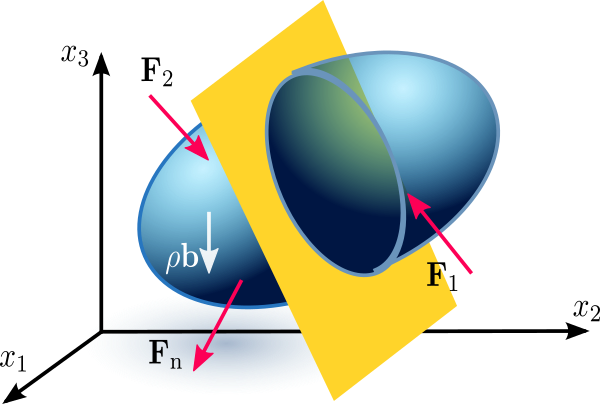
A 3D blue ellipsoid in a coordinate system is being sliced by a yellow plane. Red arrows indicate external forces acting on its surface, and a white arrow labeled ρb represents a body force like gravity.
An imaginary plane cuts through a continuous body that is subjected to external surface forces. Adapted from Wikipedia

The material on one side of the surface exerts a system of forces on the material on the other side.

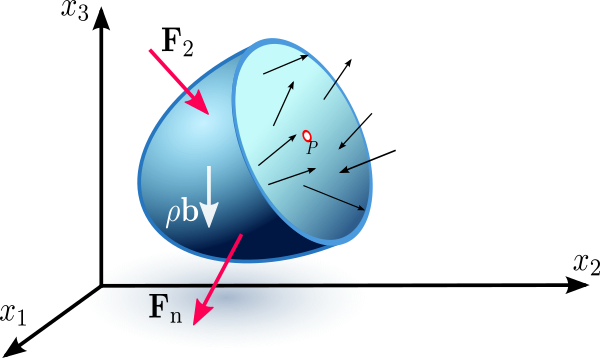
The left half of the cut blue body is shown. The flat, circular cut surface has many small black arrows pointing outwards, representing the distribution of internal forces.
One section of the body is removed, revealing a continuous distribution of internal forces acting on the newly exposed internal surface, centered at point P.

On a small area element \(\Delta S\) surrounding a point \(P\) on this surface, the resultant of the actual distribution of force on this area is a force \(\Delta \mathbf{F}\) and a moment \(\Delta \mathbf{M}\). Let \(\hat{\mathbf{n}}\) be the outward unit normal of the surface at \(P\).

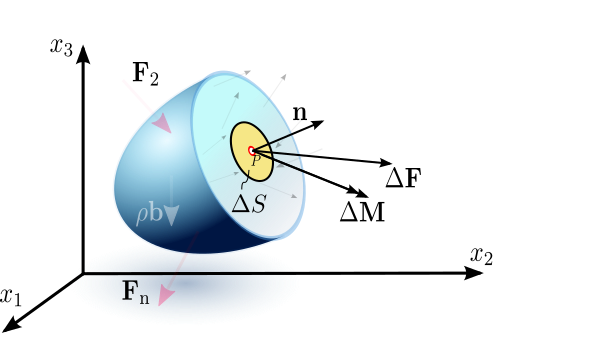
A close-up on the cut surface shows a small yellow circular area ΔS. Vectors for the resultant force ΔF, resultant moment ΔM, and the normal vector n originate from its center point P.
On a small area ΔS around point P, the distributed internal forces are represented by a resultant force ΔF and a resultant moment ΔM. The vector n is normal to the surface.

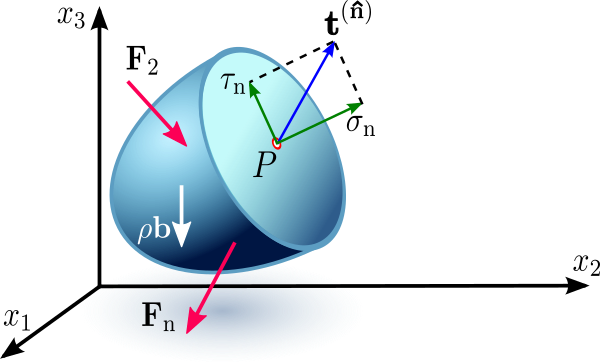
Now, we let \(\Delta S\) shrink to zero around \(P\) such that its greatest dimension also goes to zero.1 While \(\Delta\mathbf{F}\) and \(\Delta \mathbf{M}\) also go to zero, a fundamental assumption of continuum mechanics is that the ratio \(\dfrac{\Delta \mathbf{F}}{\Delta S}\) approaches a definite limit, while the effect of the moment vanishes.2 This limit of the force ratio is called the traction vector or stress vector, denoted by \(\mathbf{t}^{(\hat{\mathbf{n}})}\): \[ \mathbf{t}^{(\hat{\mathbf{n}})}=\frac{d\mathbf{F}}{dS}. \]

A close-up on the cut surface shows a small yellow circular area ΔS. Vectors for the resultant force ΔF, resultant moment ΔM, and the normal vector n originate from its center point P.
As the area shrinks to an infinitesimal point dS, the force intensity is defined as the traction vector, which is the infinitesimal force dF per unit area dS.

A stronger hypothesis, known as Cauchy’s Postulate, is also made: the traction vector \(\mathbf{t}^{(\hat{\mathbf{n}})}\) depends only on the point \(P\) and the surface’s orientation, \(\hat{\mathbf{n}}\), and is independent of the shape of the element or the surface’s curvature. The superscript \((\hat{\mathbf{n}})\) signifies this dependence on the normal vector.3

The stress vector can be resolved into two components: a normal stress \(\sigma_n\) which is perpendicular to \(\Delta S\) and a shearing stress (or shear stress) \(\tau_n\) which lies in the plane.

A sectioned body in a 3D coordinate system shows the traction vector t(n) at point P. This vector is broken down into its normal component, sigma_n, perpendicular to the surface, and its shear component, tau_n, parallel to the surface, illustrating that the traction vector is the sum of these two stress components.
The traction vector (also known as stress vector) t(n) at a point P on an internal surface is decomposed into two components: a normal stress component σn, which acts perpendicular to the surface, and a shear stress component τn, which acts parallel to the surface.
  1. Note that \(\Delta S\to 0\) is in contradiction with the fact that materials are composed of atoms and molecules, but keep in mind that (a) we assumed that the material is continuous and theres is there is no empty space between particles. (b) The above definition is very abstract and is never used in practice.↩︎
  2. A branch of continuum mechanics called couple-stress theory (or Cosserat theory) explores materials where \(\dfrac{\Delta\mathbf{M}}{\Delta S}\) does not approach zero. Instead, it approaches a limit called the couple-stress vector, which is important for modeling materials with significant internal microstructure.↩︎
  3. Note that \(\Delta S\to 0\) is in contradiction with the fact that materials are composed of atoms and molecules, but keep in mind that (a) we assumed that the material is continuous and theres is there is no empty space between particles. (b) The above definition is very abstract and is never used in practice.↩︎