Consider a rectangular cuboid of dimensions \(\Delta x\), \(\Delta y\), and \(\Delta z\).

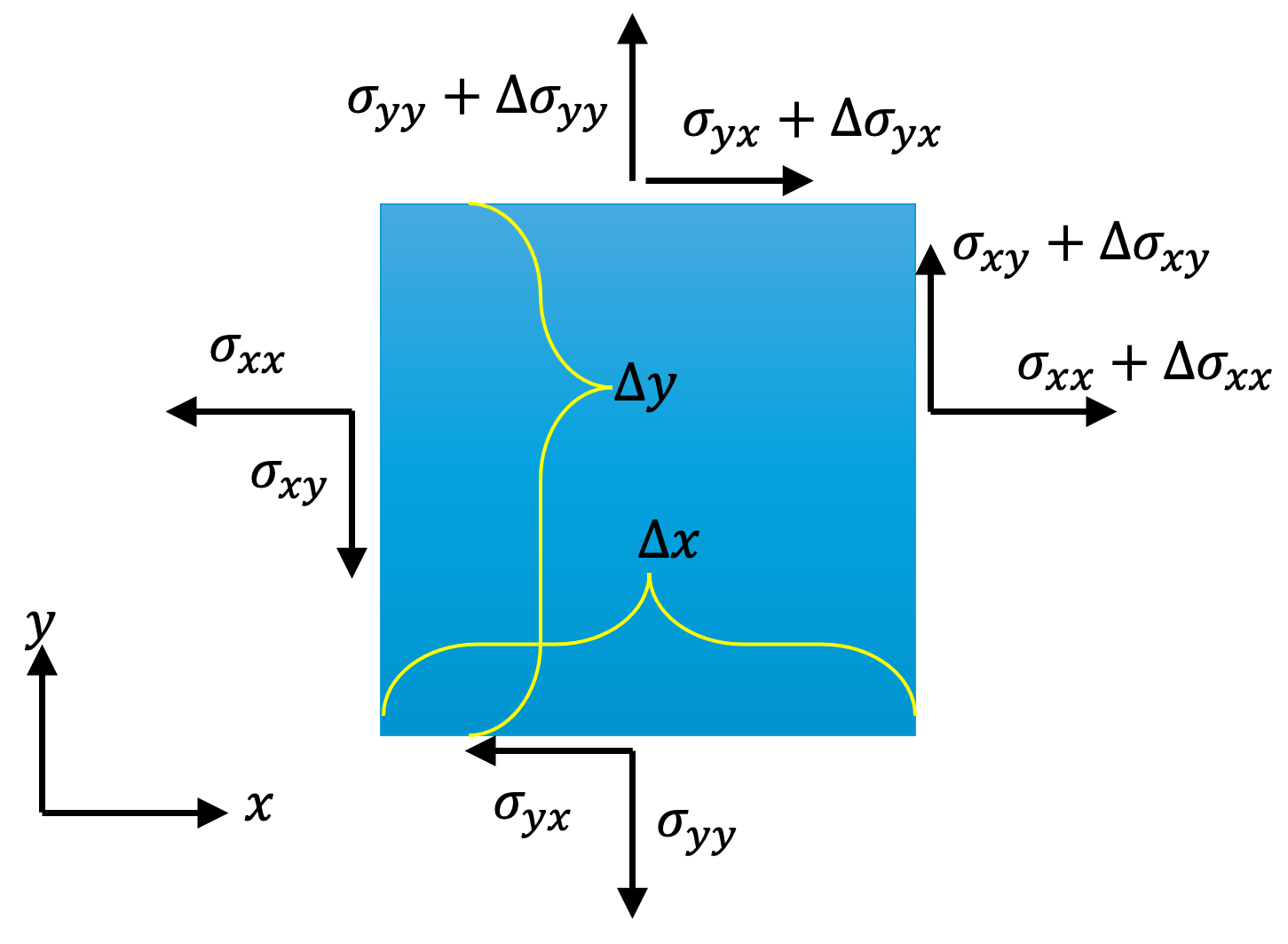
It follows from Newton’s second law for rotational motion, that \[ \sum M_z=I_{zz}\alpha_z \] where \(M_z\) is the resultant moment about the z-axis, \(I_{zz}\) is the moment of inertia (or rotational mass) about the \(z\)-axis and \(\alpha_z\) is the angular acceleration.

From statics, we recall that the moment of inertia of a rectangular block about the centroidal \(z\)-axis is \[ I_{zz}=\frac{1}{12}m [(\Delta x)^2+(\Delta y)^2] \] where \(m\) is the mass of the element. Expressing \(m\) in terms of density, we can write \[ m=\rho\, \Delta x\, \Delta y\, \Delta z \] where \(\rho\) is the mass density of the material at the point.

The components of stress that contribute to \(M_z\) are the shear stresses in the \(xy\)-plane. Body forces do not contribute to the moment. Thus, the total moment can be expressed as \[ \begin{aligned} M_z=&\left( \sigma_{x y}+\Delta \sigma_{x y}\right)(\Delta y \Delta z) \frac{\Delta x}{2}+\sigma_{x y}(\Delta y \Delta z) \frac{\Delta x}{2}\\ &-\left(\sigma_{y x}+\Delta\sigma_{y x}\right)(\Delta x \Delta z) \frac{\Delta y}{2}-\sigma_{y x}(\Delta x \Delta x) \frac{\Delta y}{2} \end{aligned} \] Equating this with the inertia expression, we obtain \[ \begin{aligned} &\frac{1}{12}\rho \Delta x \Delta y \Delta z [(\Delta x)^2+(\Delta y)^2]=\\ &\left( \sigma_{x y}+\Delta \sigma_{x y}\right)(\Delta y \Delta z) \frac{\Delta x}{2}+\sigma_{x y}(\Delta y \Delta z) \frac{\Delta x}{2}\\ &-\left(\sigma_{y x}+\Delta\sigma_{y x}\right)(\Delta x \Delta z) \frac{\Delta y}{2}-\sigma_{y x}(\Delta x \Delta x) \frac{\Delta y}{2} \end{aligned} \] Neglecting higher-order small terms, we get \[ 0=\sigma_{xy}\Delta x\Delta y\Delta z -\sigma_{yx}\Delta x\Delta y\Delta z, \] which leads to
\[ \sigma_{xy}=\sigma_{yz} \]

By applying the same logic for rotations about the x and y axes, we can prove that \(\sigma_{yz}=\sigma_{zy}\) and \(\sigma_{xz}=\sigma_{zx}\). This means that in general \[ \sigma_{ij}=\sigma_{ji} \] and the stress tensor is always symmetric, and to specify it we need only 6 independent components (instead of 9). The result holds regardless of whether the body is at rest, in uniform motion, or accelerating. ¹ This result is known as Cauchy’s Second Law of Motion.