An imaginary cut (or section) through a load bearing member can expose the internal forces. The complex distribution of forces acting over this cut surface is equipollent to a force and a moment.
We may resolve this resultant force and moment into components along the coordinate axes to study their effects. If we assume the cut is made perpendicular to the x-axis (the member’s longitudinal axis), we get six distinct internal resultants, each corresponding to a specific mode of loading:
Components of the force are: 1. Axial force (P): This force acts perpendicular to the section. It tries to either stretch or compress it. 2. Shear forces \(V_y\) and \(V_z\): These forces act parallel to the cut surface, and cause one portion of the member to slide relative to the adjacent portion.
Components of the moment are: 1. Torque or twisting moment (T) which tries to twist the member or rotate it along the x-axis 2. Bending moments \(M_y\) and \(M_z\). These moment try to bend.
These six resultants aren’t arbitrary; they are the direct mathematical sum (the integral) of the stresses acting over the entire area of the cut.
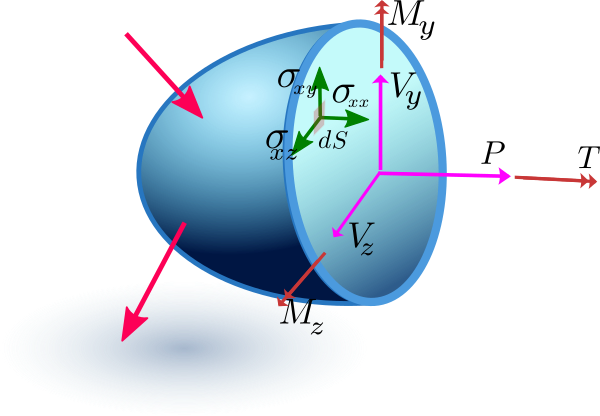
If we consider a small element on the section, then \[ dF_x=\sigma_{xx} dS,\quad dF_y=\sigma_{xy}dS,\quad dF_z=\sigma_{xz}dS \]
The sum of these forces give: \[ \begin{aligned} P=\int dF_x =\int \sigma_{xx} dS\\ V_y=\int dF_y=\int \sigma_{xy}dS\\ V_z=\int dF_z=\int \sigma_{xz} dS \end{aligned} \] Similarly, the moments generated by the stress distribution are obtained by integrating the moment of each elemental force about the section’s centroidal axes. \[ \begin{aligned} M_z&=-\int \sigma_{xx}\, y\, dS\\ M_y&=\int \sigma_{xx}\, z\, dS\\ T&=\int (\sigma_{xz} y-\sigma_{xy} z)sS \end{aligned} \]