Preface

What Is Solid Mechanics?

Solid mechanics is a branch of continuum mechanics, also known as mechanics of a continuous medium. The word “continuum” reflects the assumption that matter is considered completely continuous without any gaps or spaces between its its constituents, disregarding its atomic structure. It is clear that this assumption fails if we zoom in too closely. The level of magnification at which this assumption breaks down depends on the problem; but the is often on the scale of a few tens of nanometers. Still, sometimes it is helpful or even necessary to think about the atomic structure.

The other major branch of continuum mechanics is fluid mechanics. A solid is distinguished from a fluid by its ability to support substantial shearing forces over a specific time scale. While all materials, both fluids and solids, can support normal forces to some extent, it is this resistance to shear forces that characterizes substances like rock, steel, and rubber as solids. However, this distinction is not a clear-cut and sometimes depends on the timeframe of interest. For example, Earth’s mantle acts like a solid when seismic waves move through it quickly, but over millions of years, it flows like a fluid. Silly Putty is another example: it spreads out like a liquid if left on a table (see the following figure), but bounces like a solid when thrown at a wall (see the following video). This shows that whether a material is a solid can depend on how long the force is applied.1

Silly Putty dripping through a hole
Over several hours, Silly Putty slowly flows through an whole. Image from Wikipedia.

Silly Putty behaves like a solid when bounced. Video from Wikipedia.

Mechanics is the field of study concerning the response of bodies to forces. Therefore, the central question in solid mechanics is: how does a solid deform when a load is applied? The load can be of any type, but we mainly focus on mechanical and to some extent thermal loads. We want to determine how much (and in which direction) every particle2  moves when a load is applied. The vector function that assigns to each point of a body the displacement it undergoes when the body moves or deforms under applied loads is called the displacement field3. The gradient, or spatial derivative, of the displacement field is called strain.

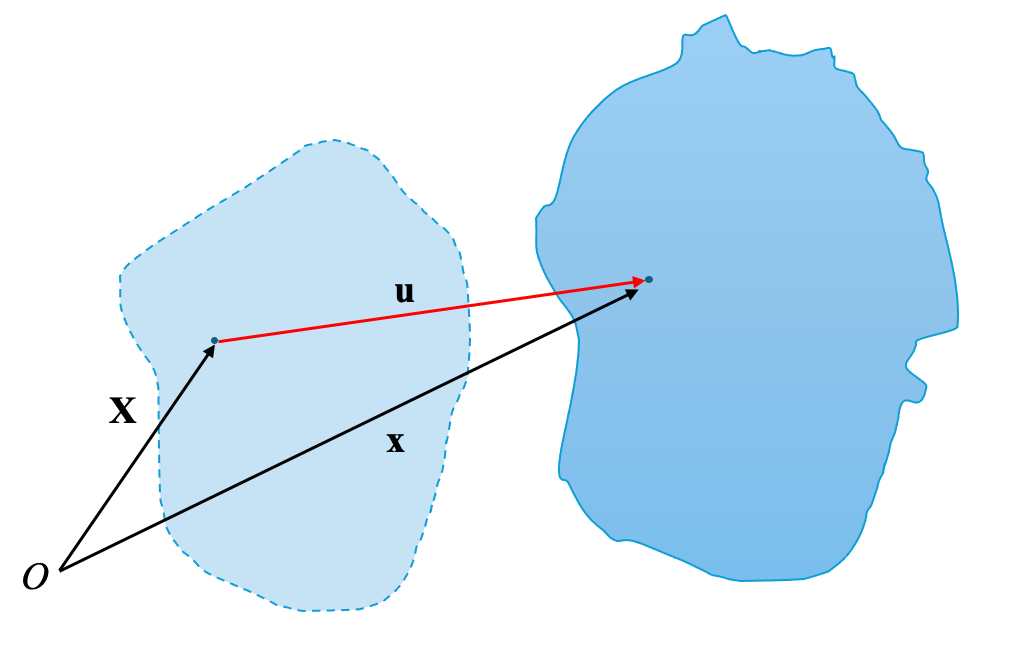
In mechanics, the displacement field is a vector function \(\mathbf{u}(\mathbf{X})=\mathbf{x}(\mathbf{X})-\mathbf{X}\) which gives, for each material point initially at position \(\mathbf{X}\) the displacement vector to its new position \(\mathbf{x}\) after deformation.

As the application of loads changes the distance between atoms, they move from their equilibrium positions, and internal forces develop. As we explained before, continuum mechanics adopts a macroscopic perspective; instead of analyzing individual atomic forces, we consider their collective effect. We speak of an average force intensity—known as stress—acting over a small volume that may contain millions of atoms. Therefore, the three fields we often work with are displacement, strain, and stress.

If, upon removing the forces, the displacement of particles returns to zero—meaning particles move back to their original places—the material is called elastic. If the strain is linearly proportional to the stress (equivalently, displacement is linearly proportional to forces), the material is considered linearly elastic. Not all elastic materials are linearly elastic. Rubber is an example of a nonlinear elastic material. If some displacement remains after the forces are removed, the remaining deformation is known as plastic deformation.

The study of the relationship between internal forces and displacement (or equivalently stress and strain) is another central topic in solid mechanics. The relationship varies from a material to another, and it is often a function of temperature and in some cases the loading rate. The study of this relationship requires some knowledge in materials science and atomic structures.

The response of a material can be time-dependent. If the load remains constant, the displacement may very gradually increase. This phenomenon is called creep. For example, a new bookshelf may be perfectly straight but can be seen to sag after bearing the weight of books for a long time. Generally creep is more severe at higher temperatures.

In some materials, the stress may decrease over time even if the displacement is held constant. This phenomenon is called stress relaxation.

stress relation
Stress relaxation is a phenomena in which although \(\epsilon\) remains constant, stress \(\sigma\) gradually decreases with time. Image from Wikipedia

A material may break into two or more separate pieces as a result of applied stress. This is what a branch of solid mechanics called fracture mechanics.

Solid mechanics is not a field that can be studied in a vacuum. A true understanding often requires knowledge of thermodynamics, materials science, or even quantum mechanics. For example, the classical theories of solid mechanics reach their limits when a metal’s internal microstructure begins to dominate its behavior. Examples of such as case include when a metal’s structure continuously evolves at high temperatures, or when it undergoes a transition from ductile to brittle. In these moments, we see a clear intersection where the principles of mechanics and materials science must work together.

Beyond the Basics: How This Book is Different

Elementary solid mechanics, also known as mechanics of materials or mechanics of deformable bodies, is a subject students typically take in their undergraduate studies. Although it introduces the concepts of stress and strain, the material is almost always assumed to be linearly elastic. In addition, only very simple cases, such as the bending of a beam or the torsion of a circular bar (shaft), are considered. This leaves open important questions, such as how to calculate the stress and strain fields when arbitrary forces are applied to a body of an arbitrary shape. Another simplification often made in elementary mechanics of materials is the assumption that the material is isotropic, meaning its properties are the same in all directions. A common example of an anisotropic material is wood, which exhibits different strengths along its fibers compared to perpendicular to them. Finally we will also study the rate-dependent behavior of materials.

In this book, we start with the analysis of stress and strain, learn about the stress-strain relationship. We derive the equations of elasticity and learn how we can solve some problems in elasticity analytically and more generally numerically. We learn about yield criteria and plastic deformation. At the end, we study elements of fracture mechanics and time-dependent behavior.

Further Studies

  1. James R. Rice. “Mechanics of Solids.” Encyclopædia Britannica. Accessed September 2, 2025. https://www.britannica.com/science/mechanics-of-solids.
  2. Dieter, George E. Mechanical Metallurgy. 1st ed. New York: McGraw-Hill, 1961.
  3. Poirier, Jean-Paul. Creep of Crystals. Cambridge University Press, 1985.
  1. Reference https://www.britannica.com/science/mechanics-of-solids by James Rice.↩︎
  2. In continuum mechanics, whenever we talk about a particle, we mean a mathematical point in space.↩︎
  3. In physics and mathematics, a field is a physical quantity that has a value for each point in space and time. Fields are classified based on the type of quantity they represent at each point. A scalar field assigns a single numerical value, or scalar (such as temperature), to every point in space. A vector field assigns a vector—a quantity with both magnitude and direction (such as velocity or displacement)—to every point. More complex quantities called tensors can also be represented by fields. A tensor field associates a tensor with every point in space and time. Stress and strain are two common examples of tensor fields that are fundamental to solid mechanics.↩︎