Consider a simply supported beam of length \(L\), height \(h\), and width \(b\). The beam is under a uniform transverse loading of intensity (force per unit length) \(w\). The intensity of the force (force per unit area) is \(q=\dfrac{w}{b}\).

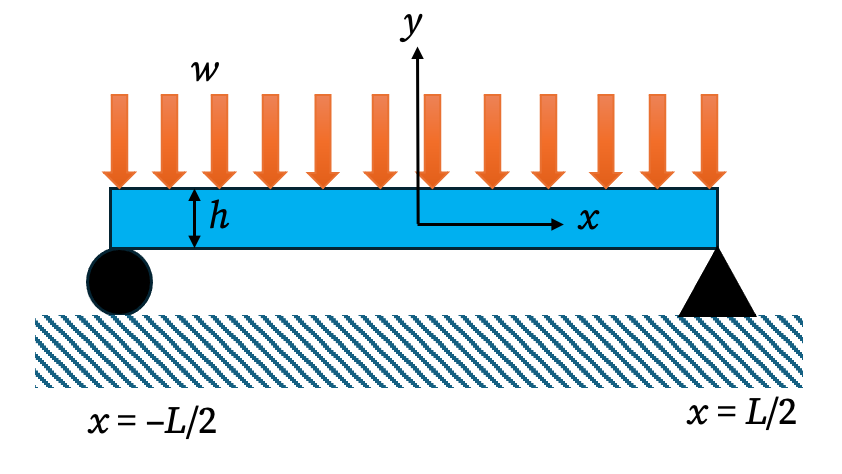
Let’s place the origin of the coordinate system at the center of the beam. The x-axis runs along the neutral axis through the length of the beam, and the y-axis runs vertically. The top and bottom surfaces are at \(y = \pm h/2\).

The boundary conditions at the upper and lower edges of the beam are: \[ \left(\sigma_{y}\right)_{y=h/2}=-q,\quad \left(\sigma_{y}\right)_{y=-h/2}=0,\quad \left(\tau_{xy}\right)_{y=\pm h/2}=0.\tag{i} \] The conditions at the ends \(x=\pm L/2\) specify the resultant forces. The total shear force must equal the support reaction (\(V = \pm wL/2\)): \[ \int_{-h/2}^{h/2} b \, \tau_{xy}\big|_{x=\pm \frac{L}{2}} dy = \pm \frac{wL}{2} \implies \int_{-h/2}^{h/2} \tau_{xy}\big|_{x=\pm \frac{L}{2}} dy = \pm \frac{qL}{2} \tag{ii} \] There is no net normal force at the ends: \[ \int \sigma_{x}\big|_{x=\pm L/2} dA=\int_{-h/2}^{h/2}b\,\sigma_{x}\big|_{x=\pm L/2} dy=0\tag{iii} \] And, because the beam is simply supported, there is no bending moment at the ends: \[ \int y \sigma_{x}\big|_{x=\pm L/2} dA=\int_{-h/2}^{h/2}by\,\sigma_{x}\big|_{x=\pm L/2} dy=0\tag{iv} \]

From the elementary theory of strength of materials, we know \(\sigma_{x}=-\frac{M(x)y}{I}\). Since the bending moment \(M(x)\) for this loading is quadratic in \(x\), we expect \(\sigma_{x}\) to contain a term proportional to \(x^2 y\). Since \(\sigma_x=\dfrac{\partial^2 \phi}{\partial y^2}\), this suggests that \(\phi\) should contain a term of the form: \[ c_1 x^2 y^3 \] This term alone would give stress components \[ \sigma_y = \frac{\partial^2 \phi}{\partial x^2} = 2c_1 y^3\quad\text{and}\quad \tau_{xy} = -\frac{\partial^2 \phi}{\partial x \partial y} = -6c_1 x y^2.\] These expressions do not satisfy the boundary conditions (i) on their own.

To satisfy the conditions \(\sigma_y\big|_{y=-h/2}=0\) and \(\sigma_y\big|_{y=h/2}=-q\), we need to add terms of the form \(\alpha y+b\) to \(\sigma_y\). This requires \(\phi\) to contain terms of the form \[ c_2 x^2y+c_3x^2. \]

Let’s try a stress function of the form: \[ \phi=c_1 x^2 y^3+c_2 x^2 y+c_3 x^2 \] Imposing the boundary conditions (i) for \(\sigma_y\) and \(\tau_{xy}\) (which also requires terms from this form of \(\phi\)) gives: \[ c_1=\frac{q}{h^3},\quad c_2=-\frac{3q}{4h},\quad c_3=-\frac{q}{4} \] and thus \[ \phi=\frac{q}{h^3}x^2 y^3-\frac{3q}{4h}x^2 y-\frac{q}{4}x^2 \] However, this function does not satisfy the biharmonic equation \(\nabla^4 \phi=0\). In fact: \[ \nabla^4 \phi =\frac{\partial^4 \phi}{\partial y^4} \left(\frac{q}{h^3}x^2 y^3\right) = \frac{24 q}{h^3}y \] To make the stress function biharmonic, we must add a term that cancels this result. A term of the form \(c_4 y^5\) will work. Substituting \(\phi=\frac{q}{h^3}x^2 y^3-\frac{3q}{4h}x^2 y-\frac{q}{4}x^2+c_4y^5\) into the biharmonic equation, we get: \[ \frac{24 q}{h^3} y+ \frac{\partial^4}{\partial y^4}(c_4 y^5) = \frac{24 q}{h^3} y + 120 c_4y=0 \] Therefore, we must have: \[ c_4=-\frac{24q}{120h^3} = -\frac{q}{5h^3} \] The improved Airy stress function is: \[ \phi = \frac{q}{h^3}x^2 y^3-\frac{3q}{4h}x^2 y-\frac{q}{4}x^2-\frac{q}{5h^3}y^5 \] This stress function gives the following stress components: \[ \begin{aligned} \sigma_{x} &= \frac{\partial^2 \phi}{\partial y^2} = \frac{6q}{h^3}x^2y - \frac{4q}{h^3}y^3 \\ \sigma_y &= \frac{\partial^2 \phi}{\partial x^2} = \frac{2q}{h^3} y^3 - \frac{3q}{2h} y - \frac{q}{2} = q\left(-\frac{1}{2}-\frac{3y}{2h}+\frac{2y^3}{h^3}\right) \\ \tau_{xy} &= -\frac{\partial^2 \phi}{\partial x \partial y} = -\frac{6q}{h^3}xy^2 + \frac{3q}{2h}x \end{aligned} \] These stress components satisfy conditions (i), (ii), and (iii). However, condition (iv) (zero moment at the ends) is violated. The moment at \(x=\pm L/2\) is: \[ \begin{aligned} M\Big|_{x=\pm L/2} &= \int_{-h/2}^{h/2}by\,\sigma_{x}\big|_{x=\pm L/2} dy \\ &= b\int_{-h/2}^{h/2}y\left(\frac{6q}{h^3}\frac{L^2}{4}y - \frac{4q}{h^3}y^3\right)dy \\ &= bq\left(\frac{L^2}{8}-\frac{h^2}{20}\right) \end{aligned} \] To cancel this unwanted moment, we must add a correction term to \(\phi\) that produces an equal and opposite moment. A term of the form \(c_5 y^3\) represents a state of pure bending. Adding \(\phi_{corr} = c_5 y^3\) gives \(\sigma_{x, corr} = 6c_5 y\). The moment produced is \(M_{corr} = \int_{-h/2}^{h/2} b y (6c_5 y) dy = \frac{bc_5 h^3}{2}\). Setting \(M+M_{corr}=0\) yields: \[ c_5 = -\frac{2}{bh^3} \left[ bq\left(\frac{L^2}{8}-\frac{h^2}{20}\right) \right] = \frac{q}{h^3}\left(\frac{h^2}{10}-\frac{L^2}{4}\right) \] Finally, our complete Airy stress function is: \[ \phi=\frac{q}{h^3}x^2 y^3-\frac{3q}{4h}x^2 y-\frac{q}{4}x^2-\frac{q}{5h^3}y^5+\frac{q}{h^3}\left(\frac{h^2}{10}-\frac{L^2}{4}\right)y^3 \] Note that the added \(y^3\) term automatically satisfies the biharmonic equation and does not contribute to \(\sigma_y\) or \(\tau_{xy}\), so conditions (i), (ii), and (iii) remain satisfied.

The final stress components are: \[ \begin{aligned} \sigma_{x}&=\frac{2q}{h^3}\left(3x^2y-2y^3-\frac{3}{4}L^2y+0.3 h^2 y\right) \\ \sigma_y &=q\left(-\frac{1}{2}-\frac{3y}{2h}+\frac{2y^3}{h^3}\right)\\ \tau_{xy} & = \frac{3qx}{2h}\left(1-\frac{4y^2}{h^2}\right) \end{aligned} \] Replacing \(q\) with \(w/b\) and noting that the moment of inertia is \(I = \frac{1}{12}bh^3\), the expression for \(\sigma_x\) can be rewritten. The bending moment from elementary theory is \[M(x)=\frac{w}{2}\left(\frac{L^2}{4}-x^2\right).\] And \[ \sigma_x=-\frac{M(x)y}{I} +\frac{w}{2I}\left(-\frac{1}{3}y^3+\frac{1}{20}h^2y\right). \] The first term is exactly the result from the elementary Euler-Bernoulli beam theory. The second term is the correction provided by the theory of elasticity. This correction term does not depend on \(x\) and is small if the beam is slender (i.e., its depth \(h\) is small compared to its span \(L\)).

The solution is exact if, at the ends \(x=\pm L/2\), the normal forces \(\sigma_x\) are distributed according to the law given by the correction term: \[ \sigma_x\Big|_{x=\pm L/2} = \frac{w}{2I}\left(-\frac{1}{3}y^3+\frac{1}{20}h^2y\right) \] These forces have no equivalent net force and no equivalent net moment. Therefore, according to Saint-Venant’s principle, the actual distribution of \(\sigma_x\) will be very close to this solution at distances from the ends greater than the depth of the beam, regardless of how the supports are actually realized.

The difference between the results of strength of materials and elasticity arises from the fact that the elementary theory assumes longitudinal fibers are in pure tension or compression (\(\sigma_y = 0\)). However, the elasticity solution shows that there are compressive stresses between fibers.

The formula for \(\tau_{xy}\) coincides with what is obtained from the strength of materials formula \(\tau_{xy} = \frac{VQ}{Ib}\).