When deriving the formulation, IVW = EVW, simply we assumed that there is only nodal forces and that’s why EVW = \(\delta \mathbf{q}^{\mathsf T}\mathbf{P}\). Now suppose that there are body forces and surface traction.

Let \(\mathbf{b}\): body force per unit mass \(\bar{\mathbf{t}}\): prescribed boundary force or surface traction per unit area. (here I have used a bar over the traction vector to indicate that it is a prescribed one)

Then \[ EVW = \int_\Omega \rho\mathbf{b}\cdot\delta \mathbf{u}\, dV+\int_{\Gamma_t}\bar{\mathbf{t}}\cdot\delta\mathbf{u}\, dS+\delta\mathbf{q}^{\mathsf T}\mathbf{P} \] which can be written as \[ EVW = \int_\Omega \rho\, \delta \mathbf{u}^{\mathsf T}\mathbf{b}\, dV+\int_{\Gamma_t}\delta\mathbf{u}^{\mathsf T}\ \bar{\mathbf{t}}\, dS+\delta\mathbf{q}^{\mathsf T}\mathbf{P} \] However, \[ \delta\mathbf{u}=\mathbf{H}\ \delta\mathbf{q} \] or \[ \{u\}=[N]\{\delta q\} \] Therefore, \[ \begin{aligned} EVW&= \int_\Omega \rho\, \delta \mathbf{q}^{\mathsf T} \mathbf{H}^{\mathsf T} \mathbf{b}\, dV+\int_\Gamma \delta\mathbf{q}^{\mathsf T}\mathbf{H}^{\mathsf T}\bar{\mathbf{t}}\, dS+\delta\mathbf{q}^{\mathsf T}\mathbf{P}\\ &=\delta \mathbf{q}^{\mathsf T} \left(\int_\Omega \rho\, \mathbf{H}^{\mathsf T} \mathbf{b}\, dV+\int_\Gamma \mathbf{H}^{\mathsf T}\bar{\mathbf{t}}\, dS+\mathbf{P}\right) \end{aligned} \]

Equating EVW = IVW gives us \[ \mathbf{K} \mathbf{q}=\mathbf{F} \] where \[ \mathbf{K}=\int_\Omega \mathbf{B}^{\mathsf T}\mathbf{E}\,\mathbf{B}\, dV \] and \[ \mathbf{F}= \int_\Omega \rho\, \mathbf{H}^{\mathsf T} \mathbf{b}\, dV+\int_\Gamma \mathbf{H}^{\mathsf T}\bar{\mathbf{t}}\, dS+\mathbf{P} \]

If the beam is loaded as in the following figure,

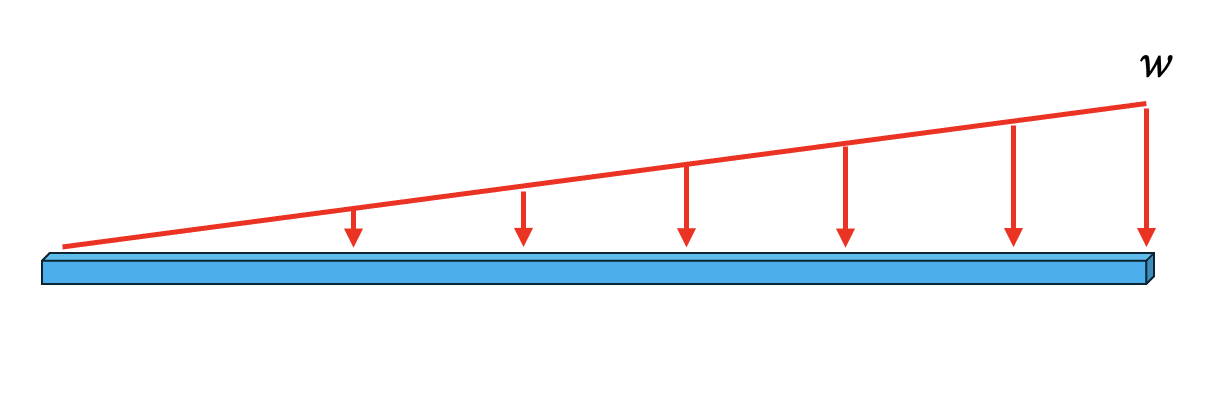
then \[ \bar{t}(x)=-\frac{w}{L}x\] and the equivalent generalized nodal forces are: \[P_1=\int_0^L N_1(x) \bar{t}(x) dx = -\frac{3wL}{20}\] \[M_1=\int_0^L N_2(x) \bar{t}(x) dx = -\frac{wL^2}{30}\] \[P_2=\int_0^L N_3(x) \bar{t}(x) dx = -\frac{7wL}{20}\] \[M_2=\int_0^L N_4(x) \bar{t}(x) dx = \frac{wL^2}{20}\] where \[ \begin{aligned} N_1(x) &= 1 - \frac{3x^2}{L^2} + \frac{2x^3}{L^3} \\ N_2(x) &= x - \frac{2x^2}{L} + \frac{x^3}{L^2} \\ N_3(x) &= \frac{3x^2}{L^2} - \frac{2x^3}{L^3} \\ N_4(x) &= -\frac{x^2}{L} + \frac{x^3}{L^2} \end{aligned} \]