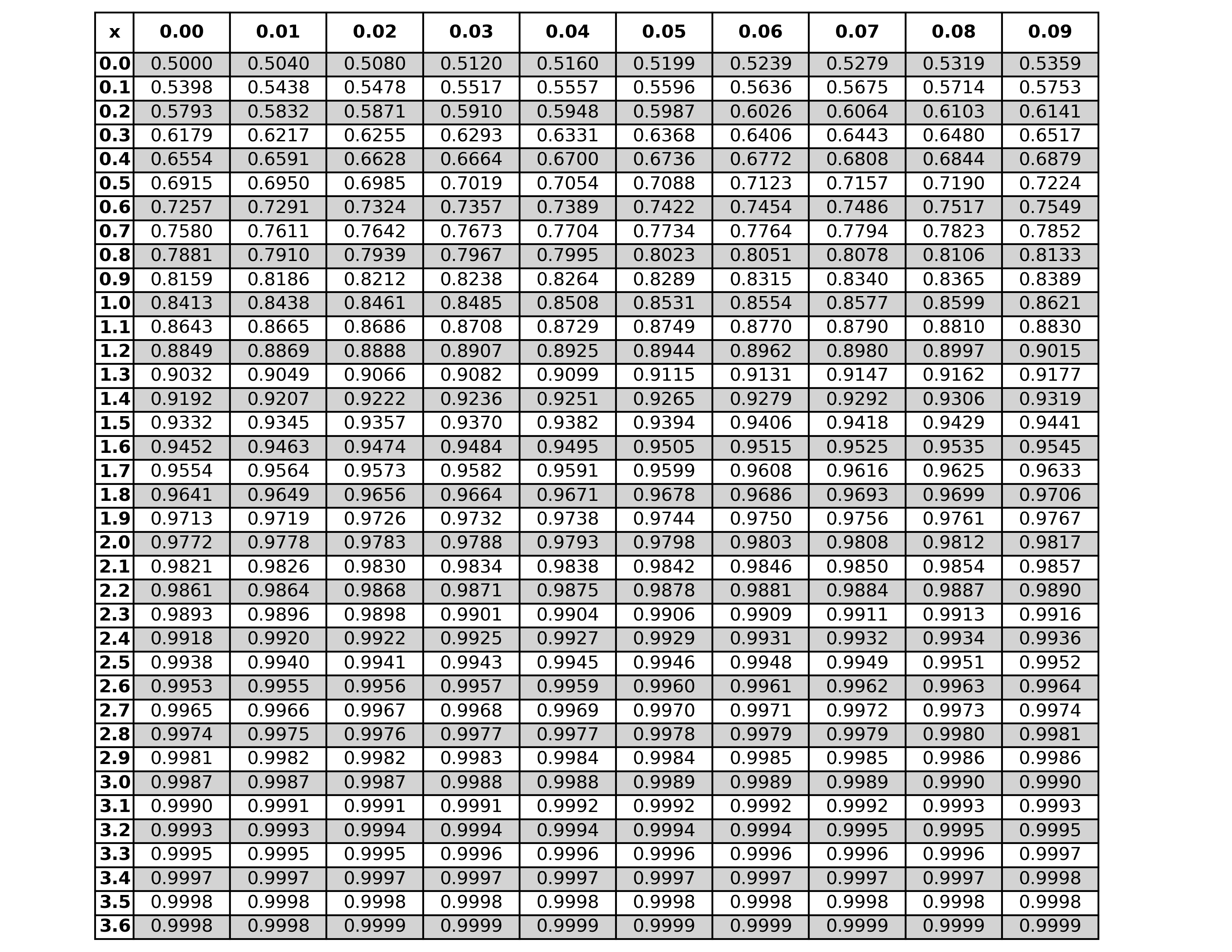
Area under the Normal Density Function
A table of \(\displaystyle \Phi(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-y^2/2} d y\)
To use the table, identify the value of \(x\) for which you want to find \(\Phi(x)\) . The table is structured with \(x\) values in increments of 0.1 along the rows and 0.01 along the columns. For example, to find \(\Phi(1.25)\) , locate the row for 1.2 and the column for 0.05. The intersection of this row and column provides the cumulative probability value, which represents \(\Phi(1.25)\) .
For negative values of \(x\) , the table can still be used by leveraging the symmetry: \[\Phi(-x)=1-\Phi(x).\]