Statics
1. A lantern of mass $M = 10$ kg is suspended above the center of a street of width $l = 10$ m by a cable. The allowable tension force in the cable is $T = 500\ \mathrm{N}$. Determine the height $H$ at which the ends of the cable should be attached if the lantern must be at a height of $h = 5$ m.
Answer
$H = h + \frac{lMg/2}{\sqrt{4T^2 - (Mg)^2}} \approx 5.5$ m.
Hint
The resultant of the cable tension forces must be equal to the weight of the lantern.
2. Is it possible to stretch a cable horizontally so that it does not sag?
Answer
No. In this case, the tension force of the rope would be infinite.
3. What should the force $F$ be in order to move a box of mass $M = 60$ kg uniformly along a horizontal surface, if the coefficient of friction between the box and the surface is $k = 0.27$, and the force is applied at an angle of $\alpha = 30^{\circ}$ to the horizontal?
Answer
$F = kMg/(\cos \alpha + k \sin \alpha) \approx 162$ N.
4. What angle $\alpha$ should the force make with the horizontal so that the force $F$ needed to move a load uniformly along a horizontal plane is minimized? The force is applied at the center of mass of the load, and the coefficient of friction is $k$.
Answer
$\alpha = \arctan k$ (see figure).
Solution
$F = \dfrac{kMg}{\cos \alpha + k \sin \alpha}$ (see problem 3).
The expression on the right-hand side is minimized when the value of the denominator $\cos \alpha + k \sin \alpha$ is maximized.
Denoting $k$ through $\tan \beta$, we can transform the expression as follows:
$
\cos \alpha + \tan \beta \sin \alpha = \dfrac{1}{\cos \beta} (\cos \alpha \cos \beta + \sin \alpha \sin \beta) = \dfrac{1}{\cos \beta} \cos (\alpha - \beta).
$
The last expression is maximized when $\cos (\alpha - \beta) = 1$, that is, when $\alpha - \beta = 0$, from which it follows that $\alpha = \beta = \arctan k$.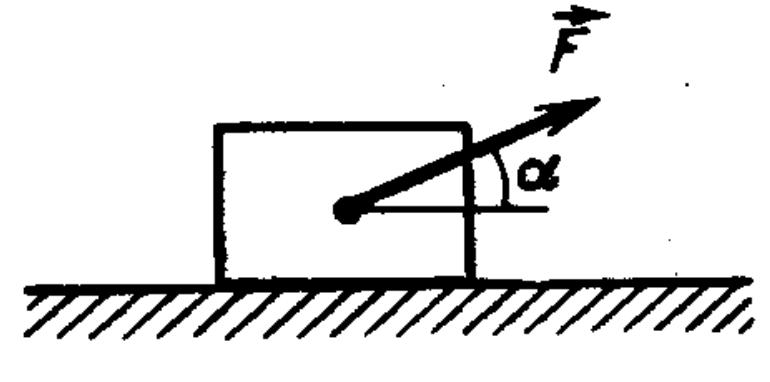
5. A spool lies on a table (see figure). In which direction will it move if a thread is pulled with force $F_1$, $F_2$, or $F_3$ (the extension of the force line of $F_2$ passes through the contact point of the spool with the table)? 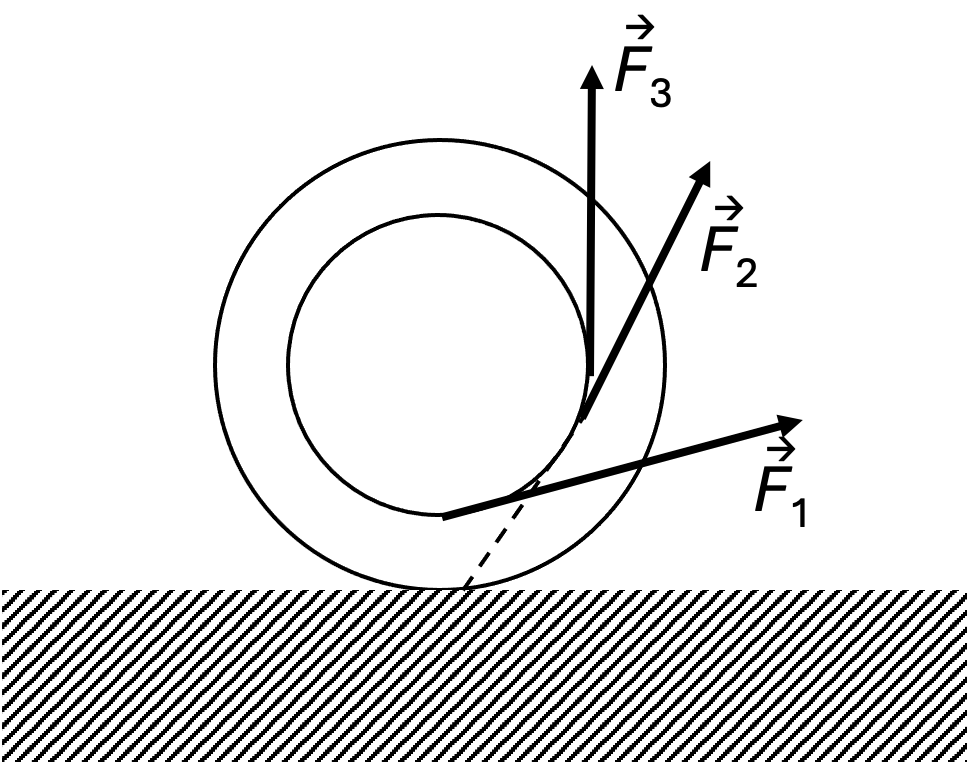
Answer
The action of the moment of force $F_1$ relative to the instantaneous axis will lead to the rotation of the spool around point O clockwise, and it will roll to the right.
The moment of force $F_2$ relative to the instantaneous axis is zero, so in this case, the thread will unwind, leaving the spool in place.
The moment of force $F_3$ will lead to the rotation of the spool counterclockwise, and it will roll to the left.
6. A rod $AB$ is hinged at point $A$ and rests with its end $B$ on a platform (see figure). What is the minimum force $F$ needed to move the platform? The mass of the rod is $m$, the coefficient of friction between the rod and the platform is $k$, and the angle the rod makes with the vertical is $\alpha$. Neglect rolling friction of the platform’s wheels and axle friction. 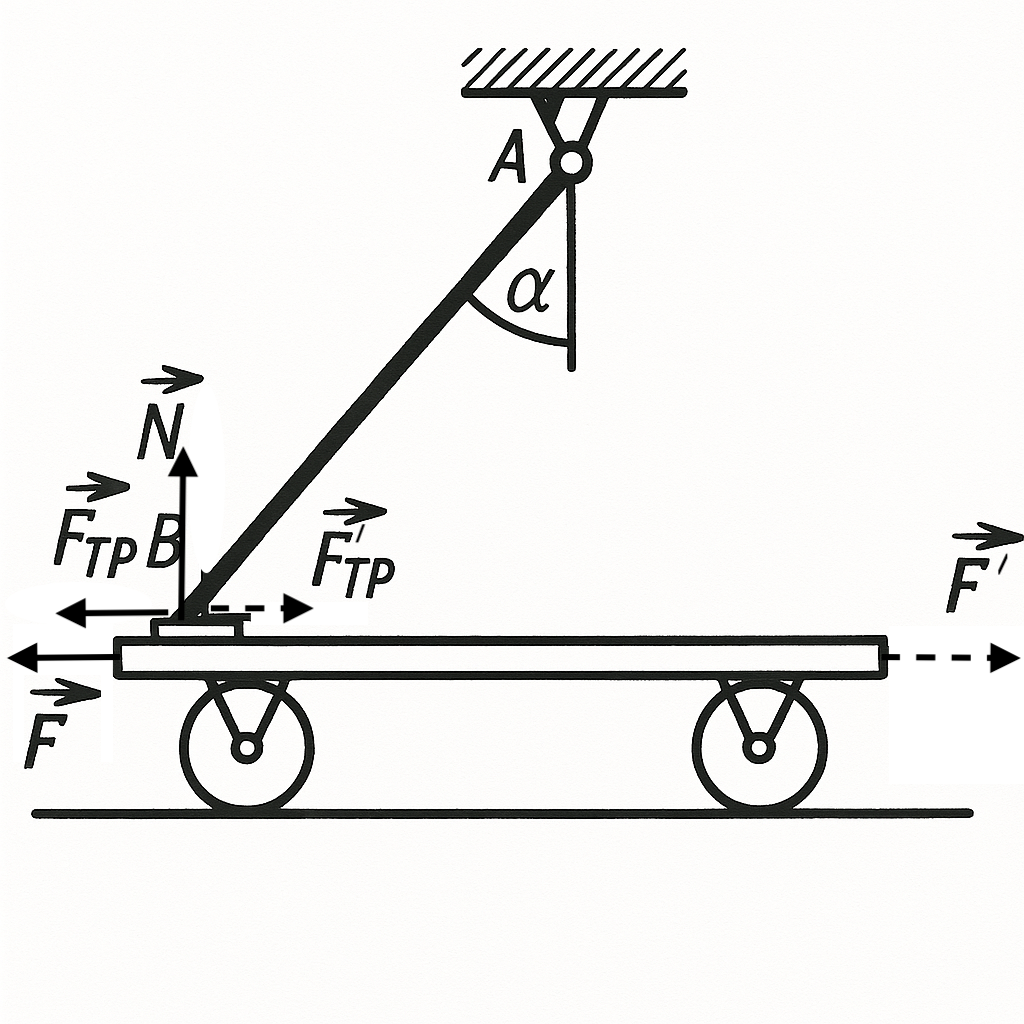
Answer
$F = \dfrac{kmg \tan \alpha}{2(k + \tan \alpha)}$ to move the cart left;
$F' = \dfrac{kmg \tan \alpha}{2(\tan \alpha - k)}$ to move it right if $\tan \alpha > k$. If $\tan \alpha < k$, it's impossible to move the cart right.
Solution
The force needed to pull the cart equals the magnitude of the friction force acting on the cart from the rod.
Consider first the case where force $F$ moves the cart left (see figure above). In this case, forces $N$ and $F_{\text{fr}}$ act on the rod, as shown in the figure. Since the rod is in equilibrium, for the moments of forces acting on it, we can write
$\frac{1}{2} mg \sin \alpha - Nl \sin \alpha - F_{\text{fr}} l \cos \alpha = 0$
($l$ is the length of the rod). Since $F_{\text{fr}} = kN$, i.e., $N = F_{\text{fr}}/k$, from this equation we find that
$F = F_{\text{fr}} = \frac{mg \sin \alpha}{2(\cos \alpha + \frac{1}{k} \sin \alpha)} = \frac{kmg \tan \alpha}{2(k + \tan \alpha)}.$
If now force $F'$ must move the cart right, the friction force acting on the rod is directed right, and from the equilibrium condition of the rod, we get
$\frac{1}{2} mg \sin \alpha - Nl \sin \alpha + F'{\text{fr}} l \cos \alpha = 0.$
Assuming the cart moves, i.e.,
$F'{\text{fr}} = kN$ or
$N = F'{\text{fr}}/k,$
we find
$F' = F'{\text{fr}} = \frac{mg \sin \alpha}{2(\sin \alpha - k \cos \alpha)} = \frac{kmg \tan \alpha}{2(\tan \alpha - k)}.$
But if $\tan \alpha < k$, $F'{\text{fr}} \to \infty$. The same happens if $\tan \alpha < k$. From the equilibrium equation of the rod, it follows that $F'{\text{fr}} = (N - mg/2) \tan \alpha$. If $\tan \alpha < k$, the friction force $F'{\text{fr}} < kN - (mg/2)k$, i.e., $F'{\text{fr}} < kN$. This means that if $\tan \alpha < k$, the friction force does not reach the value $kN$ for any value of force $F'$ applied to the cart, and it's impossible to move the cart. 'Jamming' occurs.
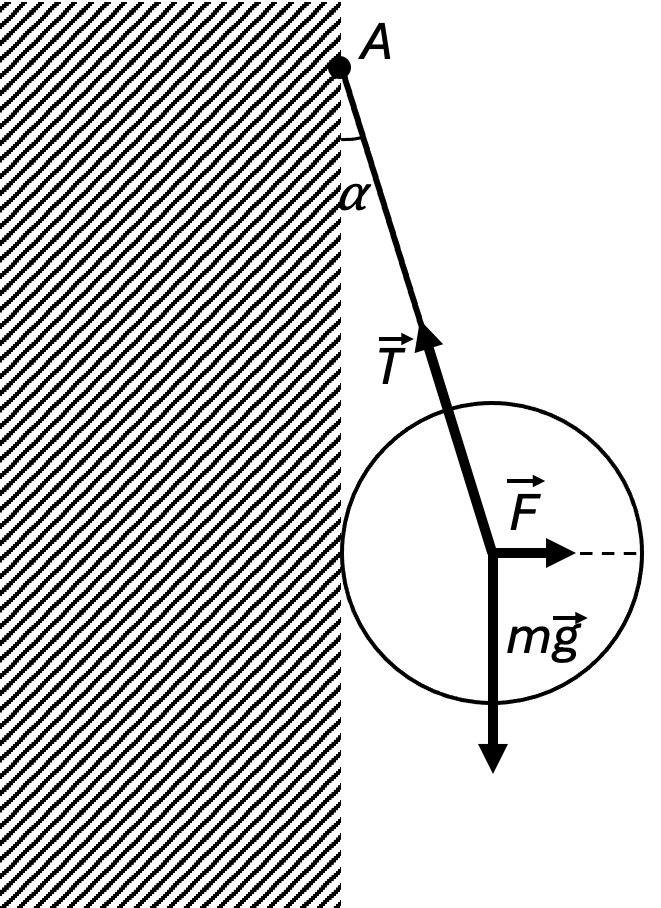
7. A ball of mass $m$ is suspended from a vertical smooth wall at point $A$ by a rope of length $l$ (see figure). What is the tension $T$ in the rope and the force $F$ exerted by the ball on the wall, if its radius is $R$? Neglect friction with the wall. 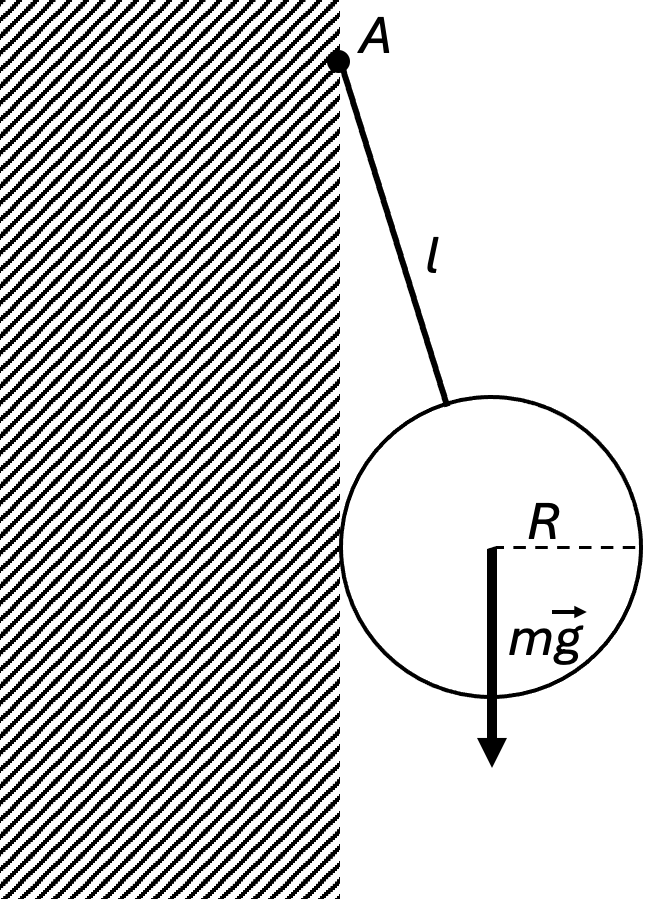
Answer
$T = mg \dfrac{l+R}{\sqrt{l^2 + 2lR}}$; $F = mg \dfrac{R}{\sqrt{l^2 + 2lR}}$.
Solution
For equilibrium of the body, two conditions must be met:
- the sum of all forces acting on the body must be zero:
$\sum \vec{F}_i = 0 \tag{1}$
(this equality must hold for the projections of all forces onto any line); - the sum of the moments of all forces acting on the body relative to any fixed axis must also be zero:
$\sum M_i = 0.$
As the fixed axis (see figure below), let's choose a horizontal line parallel to the wall and passing through the center of the sphere. Forces $\vec{F}$ and $m\vec{g}$ are directed along the radii of the sphere, so their moments relative to the chosen axis are zero. From the last condition, it follows that the moment of force $\vec{T}$ must also be zero, which means this force must be directed along the radius of the sphere. Let's now write equation (1) for the projections of forces onto the vertical and horizontal directions:
$mg - T \cos \alpha = 0,$
$F - T \sin \alpha = 0,$
where $\sin \alpha = R/(l+R)$, whence we find:
$T = mg/\cos \alpha = mg(l+R)/\sqrt{l^2+2lR};$
$F = T \sin \alpha = mg \frac{R}{\sqrt{l^2+2lR}}.$
According to Newton's third law, the pressure force of the sphere on the wall is equal in magnitude to force F and directed in the opposite direction.
8. A cylinder of radius $r$ stands on an inclined plane with angle $\alpha$ to the horizontal. What is the maximum height of the cylinder such that it does not topple, assuming it is made of a homogeneous material?
Answer
$h = 2r \cot \alpha$.
Hint
The cylinder does not tip over if the vertical line passing through the center of gravity of the cylinder passes through its base.
9. A metal bar was weighed using several dynamometers, each with a maximum load of 50 N. The total mass of the bar turned out to be 17.5 kg. How was the weighing performed and what is the minimum number of dynamometers needed?
Answer
Four dynamometers are sufficient for weighing. The sum of their readings equals the weight of the bar. The metal bar can be suspended from dynamometers located, for example, at the same distance from each other.
10. What should the coefficient of friction $k$ be so that a wedge driven into a log does not pop out? The wedge angle at the tip is $30^{\circ}$.
Answer
$k \ge \tan 15^\circ \approx 0.268$.
Hint
The force pushing the wedge out is the resultant of the reaction forces $\vec{F}_1$ and $\vec{F}_2$ of the log (see figure) (due to symmetry $|\vec{F}_1| = |\vec{F}_2|$), and the balancing force is the resultant of the friction forces $F_{fr1} = kF_1$ and $F_{fr2} = kF_2$, directed along the wedge (the force of gravity compared to these forces can be neglected). 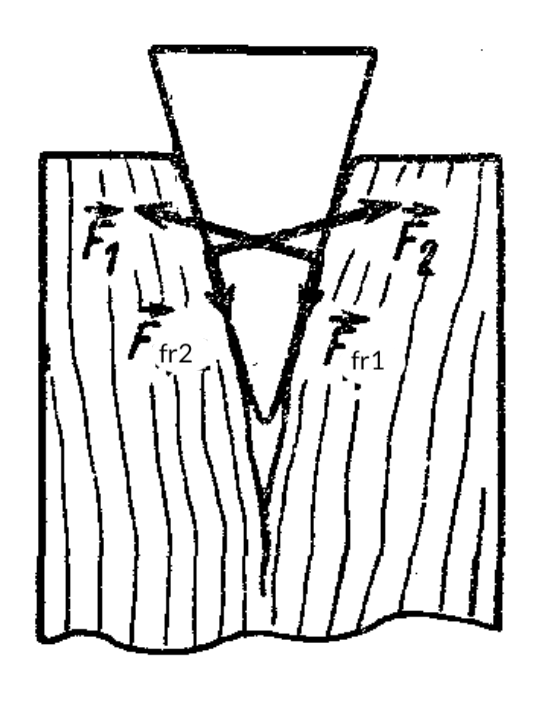
11. A pipe of mass $M = 1.2 \cdot 10^{3}$ kg lies on the ground. What force $F$ must be applied to lift the pipe from one end using a crane?
Answer
$F = Mg/2 \approx 6 \times 10^3$ N.
12. A car with a mass of 1.35 tons has a wheelbase length of $3.05\ \mathrm{m}$. Its center of gravity is located 1.78 m behind the front axle. Determine the force acting on each of the front wheels and each of the rear wheels from the horizontal surface.
Answer
2754 N on the front wheels and 3861 N on the rear wheels.
13. A mass $m$ is suspended from two identical springs, once connected in series and once in parallel (see figure). Find the extension $\Delta x$ of the springs in both cases if the stiffness of each spring is $k$. Will the distance $\Delta l$ by which the load descends be the same in both cases? 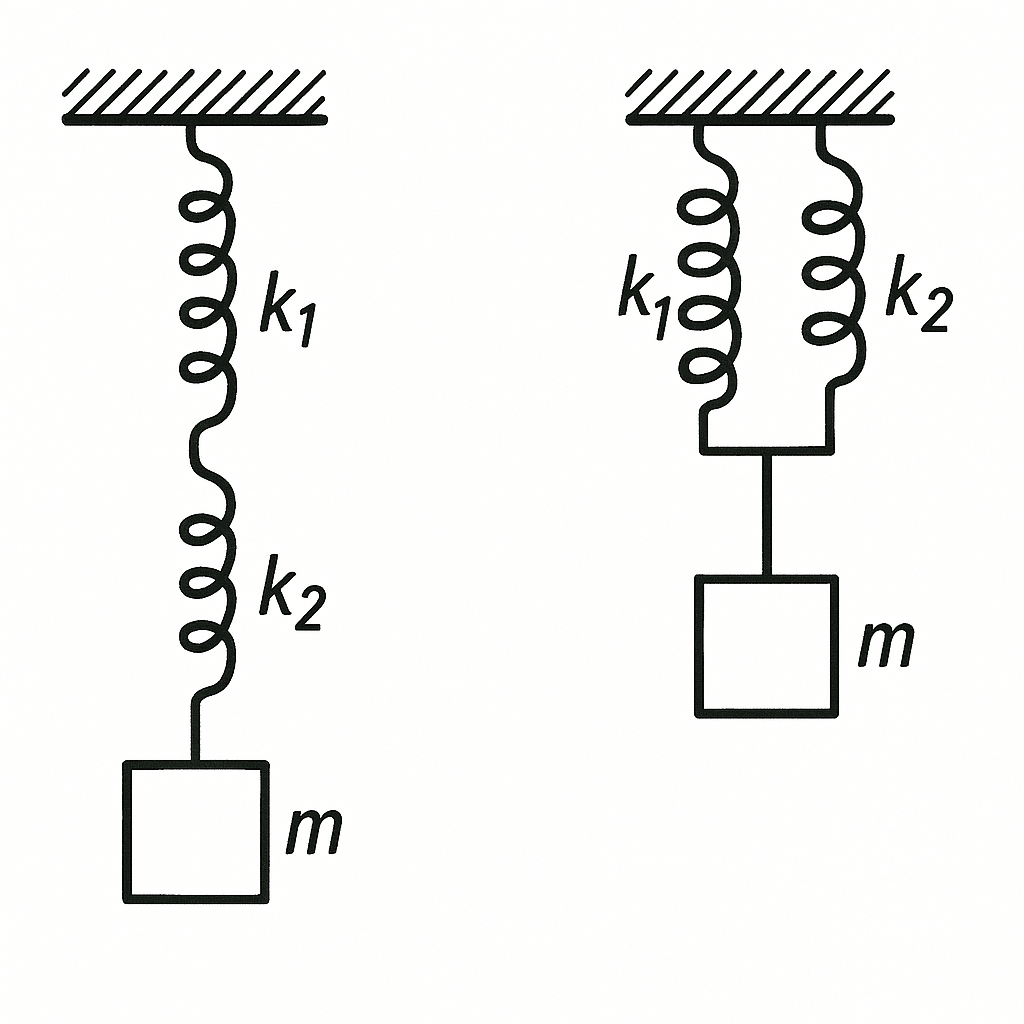
Answer
a) $\Delta x = mg/k$; $\Delta l = 2\Delta x$;
b) $\Delta x = mg/(2k)$; $\Delta l = \Delta x$.
14. Two springs with stiffness coefficients $k_1$ and $k_2$ are connected once in series and once in parallel (see figure). What should be the equivalent stiffness $k_{\text{eq}}$ of a single spring that could replace the system of two springs? 
Answer
$k_{eq} = k_1 k_2 / (k_1 + k_2)$ for series connection of springs and $k_{eq} = k_1 + k_2$ for parallel connection.
Solution
In series connection of springs, the forces stretching them are equal and equal to the force F stretching the system of springs, and the extension of the system is equal to the sum of the extensions of the springs: $\Delta x = \Delta x_1 + \Delta x_2.$ Since $F = \Delta x k_{eq}$, then $\Delta x = F/k_{eq}.$ Similarly, $\Delta x_1 = F/k_1$ and $\Delta x_2 = F/k_2$. Therefore $\frac{1}{k_{eq}} = \frac{1}{k_1} + \frac{1}{k_2}$ and $k_{eq} = \frac{k_1 k_2}{k_1 + k_2}.$ In parallel connection of springs $\Delta x = \Delta x_1 = \Delta x_2$, and $F = F_1 + F_2$. Substituting $F = \Delta x k_{eq}$, $F_1 = \Delta x k_1$ and $F_2 = \Delta x k_2$ here, we get $k_{eq} = k_1 + k_2.$
15. A mass $m$ is suspended from the end of a spring of initial length $l$, causing the spring to stretch by $0.1\,l$. At what point along the unstretched spring should a mass of $2m$ be suspended so that its attachment point is equidistant from the spring’s ends? The mass $m$ remains attached to the lower end of the spring. Neglect the mass of the spring.
Answer
$l_1/l_2 = 11/13$.
Solution
Let $l_1$ and $l_2$ be the lengths of the parts into which the inextensible spring is divided by point A, where a mass $2m$ needs to be suspended, and $k_1$ and $k_2$ be the stiffnesses of these parts of the spring. Since when suspending a weight, the extension of the whole spring is $n$ times greater than the extension of the $1/n$ part of this spring, the stiffness of the whole spring is $n$ times less than the stiffness of the $1/n$ part of the spring (see problem 14), i.e., $k_1 = lk/l_1\quad\text{and}\quad k_2 = lk/l_2,$ where $k = mg/(0.1l)$. When suspending a mass $2m$, a weight $3m$ will act on the upper part of the spring and it will extend by $\Delta l_1 = \frac{3mg}{k_1} = 3mg \frac{l_1 } {lk}.$ The lower part of the spring will extend by $\Delta l_2 = mg/k_2 = mg \frac{l_2}{lk},$ while $l_1 + \Delta l_1 = l_2 + \Delta l_2,$ i.e., $l_1 (\frac{3mg}{lk} + 1) = l_2 (\frac{mg}{lk} + 1).$ Hence $\frac{l_1}{l_2} = \frac{mg+lk}{3mg+lk} = \frac{mg + mg/0.1}{3mg + mg/0.1} = \frac{11}{13}.$
16. What is the minimum coefficient of friction $k_{\text{min}}$ between the walls of a cube and a horizontal surface so that the cube can be tipped over an edge using a horizontal force applied to the top face? What should the applied force $F$ be? The mass of the cube is $M$.
Answer
$F > Mg/2$, $k_{min} = 1/2$.
Hint
Apply the second condition (see problem 7), choosing the edge about which the cube rotates as the fixed axis. The maximum friction force must be no less than the force F applied to the body.
17. What is the minimum force $F_{\text{min}}$ required to tip a cube over an edge on a horizontal surface? What must be the minimum coefficient of friction $k$ between the cube and the surface? The mass of the cube is $M$.
Answer
$F_{min} = Mg\sqrt{2}/4$; $k \ge 1/3$.
Hint
The force required to tip the cube is minimal if it is perpendicular to the diagonal plane passing through the edge about which the cube tips, and is applied to the second edge of the cube lying in this diagonal plane.
18. A tall rectangular block with a square base stands on a horizontal surface. How can the coefficient of friction between the block and the surface be approximately determined using only a ruler?
Answer
Solution: If a horizontal force $F=kmg$ is applied to the block near its base, it will start moving. If this force is applied at height $h$ from the floor, then $Fh = mga/2$ and it will start tipping over around the edge of the base. Therefore $kmgh = mga/2$ and $k = a/(2h)$; $a$ is the side of the base.
19. An iron rod of mass $M$ is bent in half so that its two parts form a right angle (see figure). The rod is suspended by one end on a hinge. Find the angle $\alpha$ that the upper part of the rod makes with the vertical in the equilibrium position. 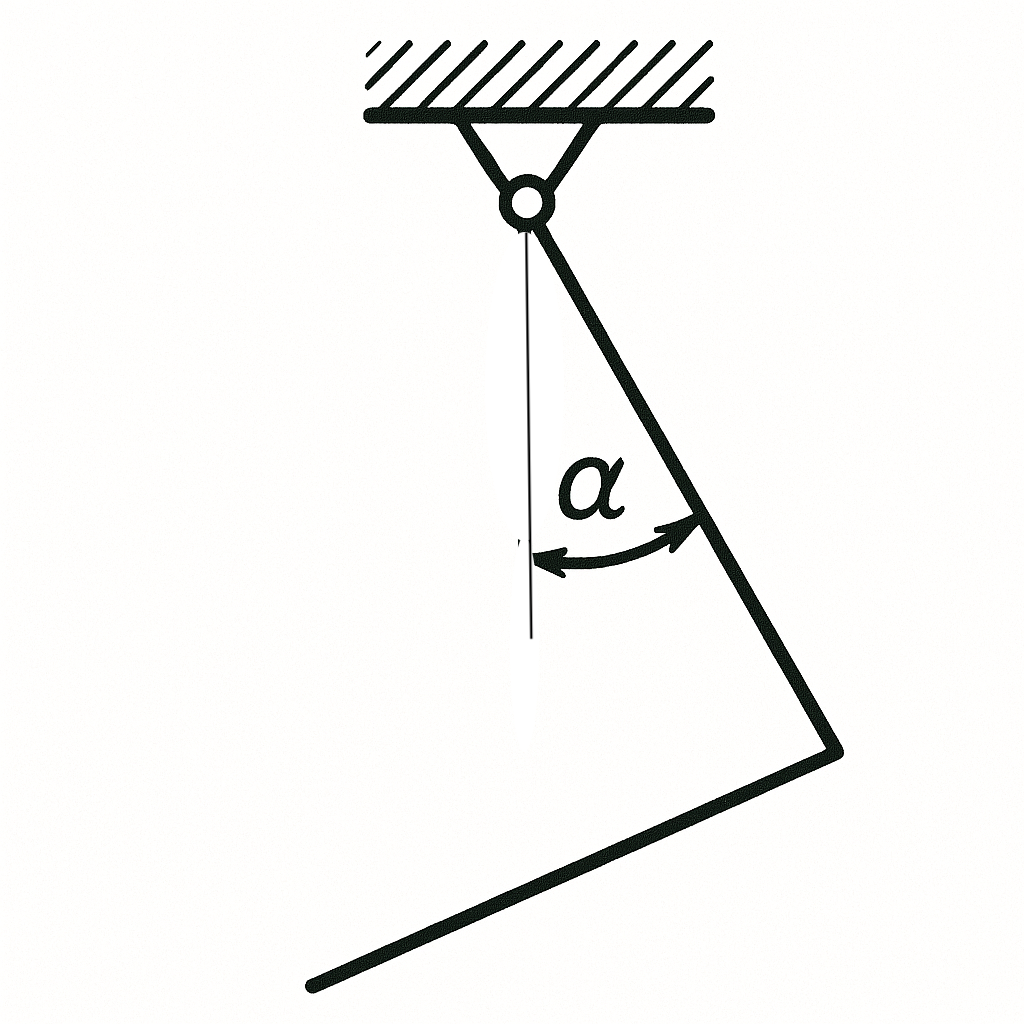
Answer
$\tan \alpha = 1/3$.
Hint
The rod will hang such that the vertical line passing through the suspension point A of the rod passes through its center of gravity O (see figure). Let the length of the rod be $2l$, find the lengths of the segments: $AB = l/2 + DB = l/2 + l/4 = \frac{3l}{4}$ and $OB = l/4.$ 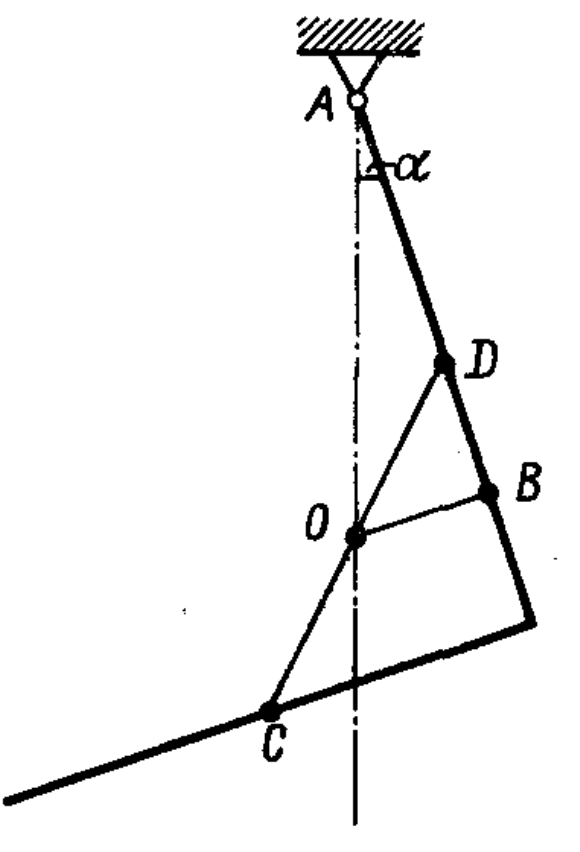
20. A uniform beam of mass $M$ and length $l$ is suspended by its ends on two springs (see figure). Both springs have the same length when unloaded, but the stiffness of the left spring is $n$ times greater than that of the right spring (under equal loads, the extension of the right spring is $n$ times that of the left). At what distance $x$ from the left end of the beam should a mass $m$ be suspended to keep the beam horizontal? Assume $n = 2$. 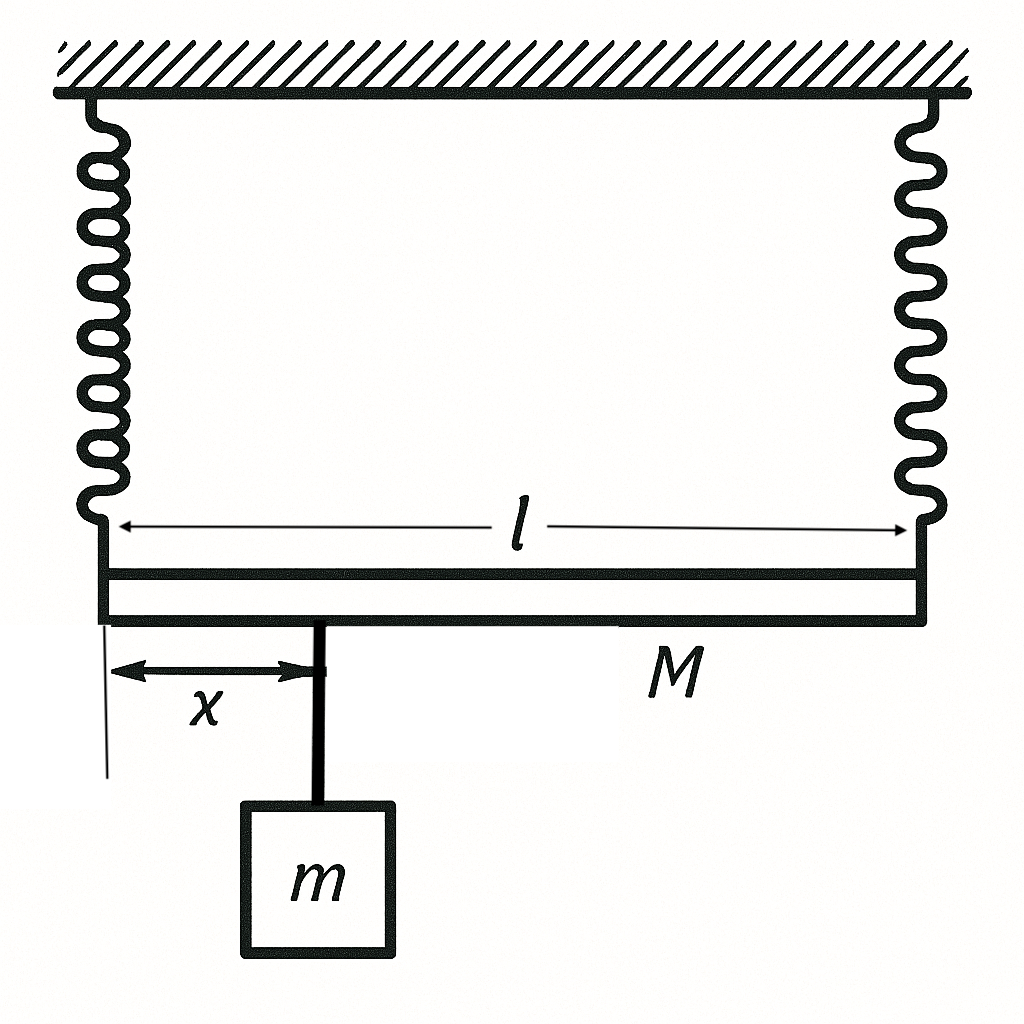
Answer
$x = l \frac{M(n-1)+2mn}{2m(n+1)}$.
Hint
The extensions of the springs must be the same. The force $F_1 = \frac{Mg}{2} + \frac{l-x}{l} mg$ acts on the left spring at equilibrium, and the force $F_2 = \frac{Mg}{2} + \frac{x}{l} mg$ acts on the right spring (see figure above).
21. A ball of mass $m = 4.9$ kg rests between two smooth inclined planes. The left plane forms an angle $\alpha = 35^{\circ}$ with the horizontal, and the right plane an angle $\beta = 20^{\circ}$. Find the forces $F_1$ and $F_2$ that the ball exerts on the planes. Solve the problem in two ways: a) by resolving forces and b) using the moment method.
Answer
$F_1 = mg \sin \beta / \sin(\alpha + \beta) = 20$ H; $F_2 = mg \sin \alpha / \sin(\alpha + \beta) = 34$ H.
Hint
As fixed axes, it is convenient to choose horizontal lines passing through the points of contact of the sphere with the planes.
22. A wheel of radius $R$ and mass $m$ stands before a step of height $h$. What is the minimum horizontal force $F$ that must be applied to the axle $O$ of the wheel for it to climb the step? Neglect friction.
Answer
$F \ge mg \frac{\sqrt{h(2R-h)}}{R-h}$.
Hint
For the wheel to roll over the step, the moment of the force $\vec{F}$ applied to the wheel relative to the axis passing through point A (see figure) must be greater than or equal to the moment of the gravity force $m\vec{g}$ of the wheel relative to the same axis. 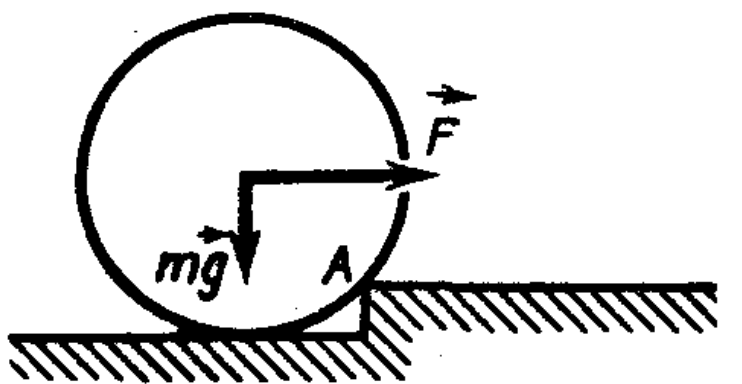
23. Which is easier: to move a stationary railway car by pushing on its body or by pushing at the top of a wheel's rim?
Answer
To the rim of the wheel. In this case, the moment of the applied force is twice as large.
24. Why does the front of a car dip down during sudden braking?
Answer
During braking, the friction force $F_{\text{fr}}$ acts on the car wheels. Let's apply forces $\vec{F}_1$ and $\vec{F}_2$ to the center of gravity of the car, equal to $F_{\text{fr}}$ and directed in different directions (see figure). This can be done, since the sum of these forces and their moments relative to any axis are zero.
Now $\vec{F}1$ can be considered as the braking force, and $F{\text{fr}}$ and $\vec{F}_2$ as a couple of forces causing the car to rotate around the axis passing through the point of contact of the wheels with the road, as a result of which the front end of the car lowers.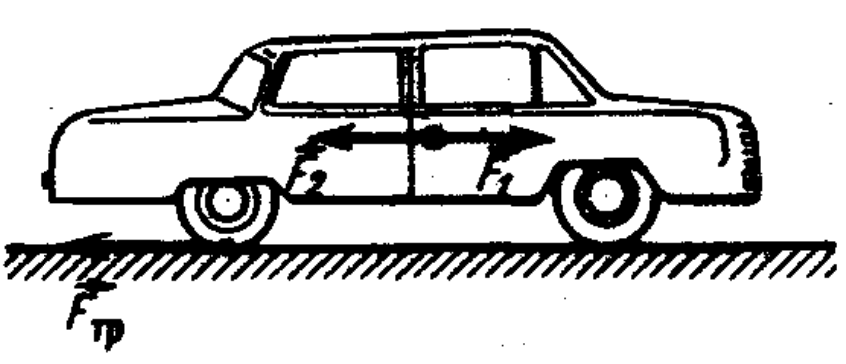
25. A wooden plate floats on water. A couple of forces (equal and opposite but not along the same line) is applied horizontally. Around which point does the plate rotate?
Answer
The couple of forces will cause the plate to rotate around its center of mass.
Hint
Since the sum of the forces acting on the plate is zero, its center of mass will remain at rest.
26. A heavy uniform board of mass $M$ and length $l$ leans against a corner between the wall and floor, with a rope attached to the other end. Determine the tension force $F$ in the rope if the angle between the board and rope is $\beta = 90^{\circ}$. How does this force change as the angle $\alpha$ between the board and floor increases, keeping $\beta$ constant?
Answer
$F = 0.5 Mg \cos \alpha$; decreases.
27. A ladder of mass $m$ leans against a smooth vertical wall, forming an angle $\alpha$ with the horizontal floor. Its center of gravity is at the midpoint. What are the directions and magnitudes of the forces acting on the ladder from the wall and floor? Use construction to find the direction of the reaction from the floor.
Answer
$N_A = \dfrac{mg}{2} \cot \alpha$; $Q = \dfrac{mg}{2} \sqrt{4 + \cot^2 \alpha}$.
Solution
Let's write the equilibrium conditions for the ladder (see problem 7; see figure).
1st condition: $x$-axis: $N_A - F_{\text{fr}} = 0$; y-axis: $N_B - mg = 0$;
2nd condition: for moments of forces relative to the horizontal axis passing through the points of contact of the ladder with the support,
$N_A l \sin \alpha = mgl \cos \alpha / 2.$
The resultant of forces $N_B$ and $F_{\text{fr}}$ is
$Q = mg/2 \sqrt{4 + \cot^2 \alpha}.$
Force $Q$ must pass through point O of intersection of the lines passing through forces $N_A$ and $mg$, since the sum of the moments of all forces relative to this point must be zero (see figure).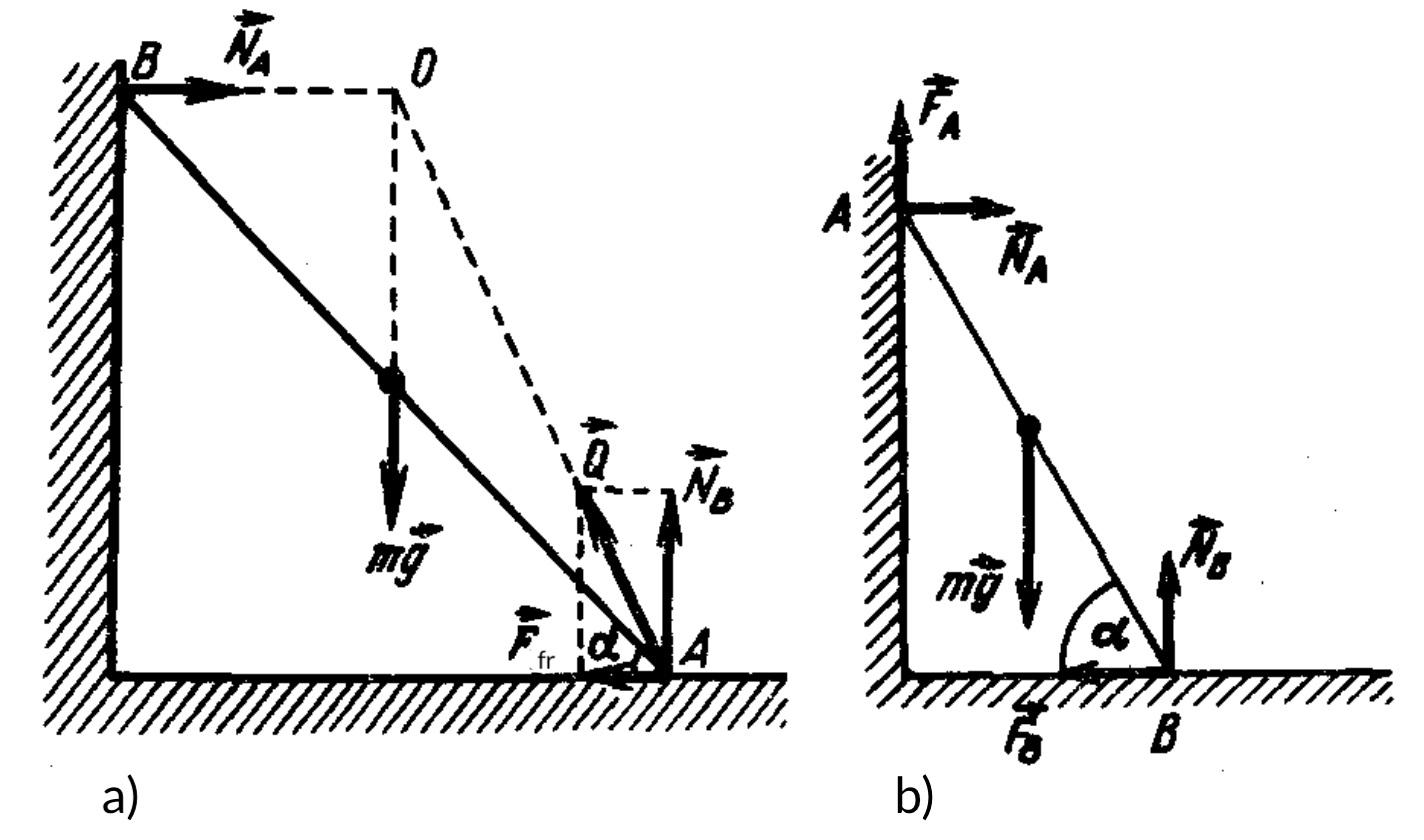
28. A rod $AB$ of mass $m = 5$ kg is hinged at point $A$ and can rotate in a vertical plane (see figure). A thread is attached to point $B$ and runs over pulley $C$ with a mass $m_1 = 2.5$ kg hanging from it. The axes of pulley $C$ and hinge $A$ lie on the same vertical line, and $AC = AB$. Find the angle $\alpha$ between the rod and vertical at equilibrium. What is the force $F_{AB}$ along the rod at point $A$? Is the equilibrium stable? 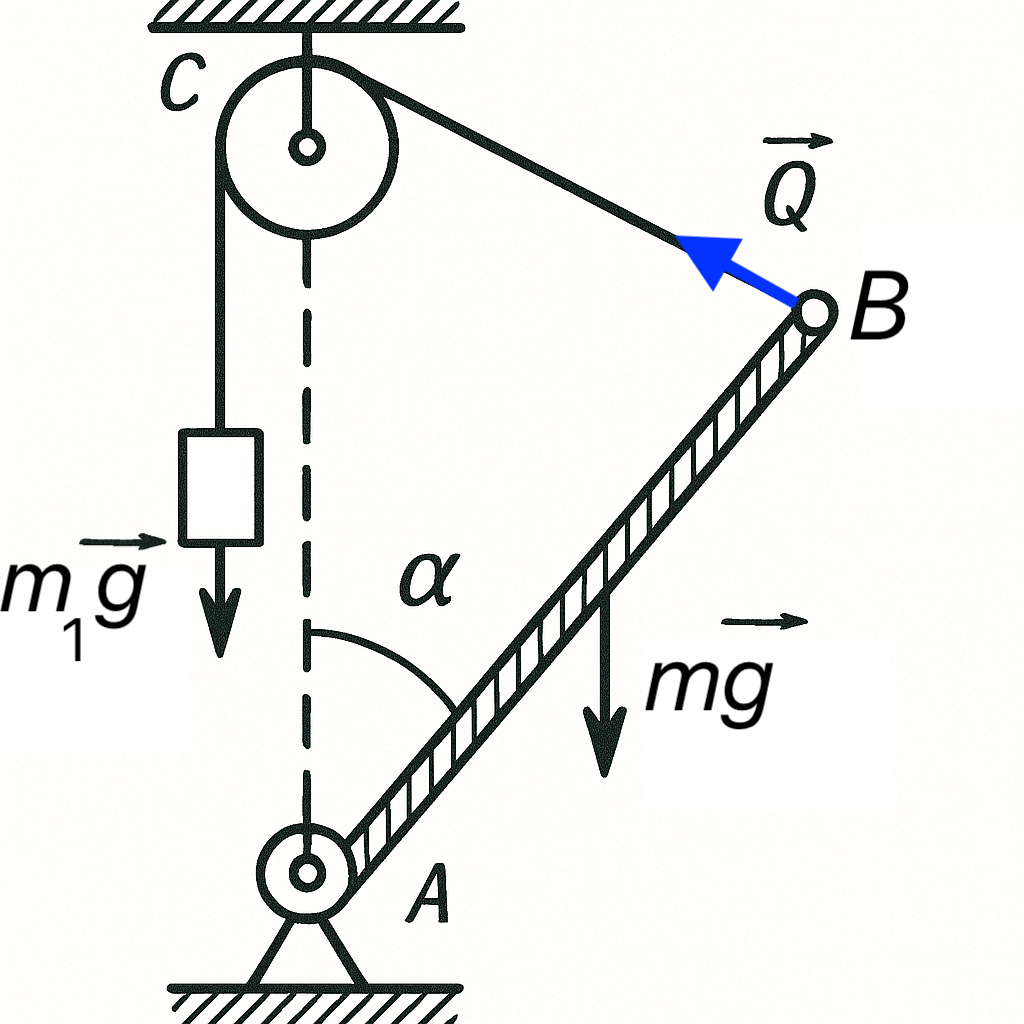
Answer
$\sin(\alpha/2) = m_1/m$; $\alpha = 60^\circ$; $F_{AB} = mg \cos^2(\alpha/2) \approx 36.75$ N; unstable equilibrium.
Hint
To determine the angle $\alpha$, consider the moments of the forces acting on the rod $Q=m_1 g$ and $mg$ relative to point A (see figure above). Having considered the moments of the forces acting on the rod relative to point C, find the force $F_A$ acting in the hinge A (see problem 27; the line of action of force $F_A$ passes through the intersection point of the lines of action of forces $Q$ and $mg$, lying on the midpoint of side BC of the equilateral triangle ABC): $F_A l \sin(\alpha/2) = mgl \sin \alpha / 2 \implies F_A = mg \cos(\alpha/2).$ Its projection onto the direction of the rod $F_{AB} = F_A \cos(\alpha/2)$. The equilibrium is unstable: for any small deviation from the found position of equilibrium, the system cannot return to it on its own, moreover, the changed ratio of the moments of forces acting on the rod will contribute to the further displacement of the system in the same direction.
29. A ladder stands against a wall. The friction coefficient with the wall is $k_1 = 0.4$ and with the ground is $k_2 = 0.5$. The ladder's center of gravity is at its midpoint. Find the minimum angle $\alpha$ the ladder can make with the horizontal without slipping.
Answer
$\alpha_{min} = \arctan \frac{(1-k_1 k_2)}{2k_2} \approx 38^\circ 40'$.
Hint
See the solution to problem 27. The forces acting on the ladder are shown in the following figure. The limiting angle $\alpha_{min}$, which the ladder can form with the horizon without slipping, will correspond to the maximum possible static friction forces $F_A$ and $F_{\text{fr}}$, i.e., they must simultaneously have the largest possible values, equal respectively to $k_1 N_A$ and $k_2 N_B$. 
30. A ladder of length $l = 4$ m leans against a smooth wall at an angle $\alpha = 60^{\circ}$ with the floor. The maximum friction force between the ladder and the floor is $F_{\text{fr}} = 200\ \mathrm{N}$. How high $h$ can a person of mass $m = 60$ kg climb before the ladder starts to slip? Neglect the ladder’s mass.
Answer
$h = l F_{\text{fr}} \sin \alpha \tan \alpha / (mg) \approx 2$ m.
Hint
See problem 27. The forces acting on the ladder are shown below. 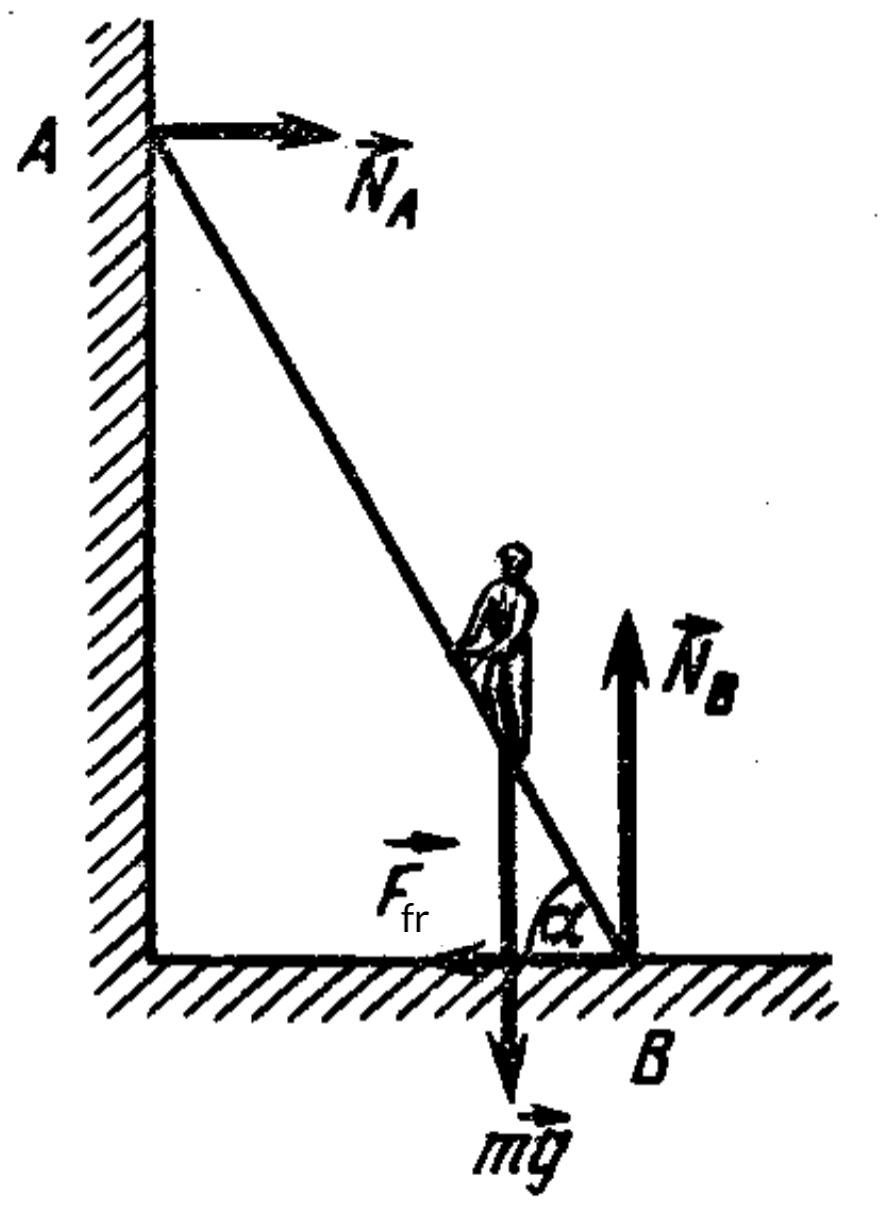
31. A cube is placed near a wall so that one of its faces makes an angle $\alpha$ with the floor. What coefficient of friction with the floor is required for this to be possible, assuming negligible friction with the wall?
Answer
For $k \ge 1/2 (\cot \alpha - 1)$.
Hint
Write down the condition for the sum of moments of the reaction forces of the wall and the force of gravity relative to the axis passing through the line of contact of the cube with the floor to be zero, and take into account that the reaction force of the wall must be equal in magnitude to the friction force $kN_1$, and the force $N_1$ is the reaction force of the floor, equal to the force of gravity.
32. 1. A rod hangs horizontally on a rope loop. Will equilibrium be disturbed if the rod is bent to the right of the loop?
- Suppose the rod is thicker on one side. Are the masses to the left and right of the loop equal?
Answer
1. Will be disturbed.
- The mass of the thick end of the rod is greater.
33. Prove that the center of gravity of a flat triangle lies at the intersection point of its medians.
Answer
Hint: By lines parallel to any of the sides, the triangle is divided into thin strips. Obviously, the center of gravity of the triangle lies on the line passing through the midpoints of these strips, i.e., on the median.
34. Prove that the center of gravity of a triangle made of uniform thin rods lies at the center of the incircle of a triangle whose vertices are midpoints of the original triangle’s sides.
Hint
The center of mass of each rod lies at its midpoint. Connecting the midpoints of the rods, we get a triangle whose side lengths are half the side lengths of the given triangle and, consequently, proportional to the masses of the corresponding rods. The angle bisectors of the resulting triangle divide its sides into parts proportional to the other two sides.
35. Ten spheres with masses $1, 2, 3, \ldots, 10$ g are fixed along a weightless rod of length 90 cm, spaced 10 cm apart. Find the center of mass of the system.
Answer
At a distance of 30 cm from the 10 g ball.
Hint
The system will be balanced if a force equal to the sum of the weights of the balls is applied to the center of mass of the system. Write down the condition for the sum of moments of all forces acting on the system relative to one of the endpoints to be zero, find the position of the center of mass.
36. A uniform thin plate is shaped like a circle of radius $R$, with a circular hole of half the radius cut from it, touching its edge. Where is the center of gravity?
Answer
$R/6$ from the center.
Solution
Let the distance from the center of mass of the plate to the center of the circle be $x$. From symmetry considerations, it is obvious that the center of mass of the plate lies on its diameter passing through the center of the hole (see figure). If we fill the hole with the material from which the plate is made, the center of the resulting solid plate will be at the center of the circle. Therefore, the equality $m_1 R/2 = x m_2$ must hold. Substituting $m_1 = \pi (R/2)^2 \rho = \pi R^2 \rho / 4$ and $m_2 = \pi R^2 \rho - m_1 = 3/4 \pi R^2 \rho$ here, where $\rho$ is the surface density of the plate material, we get $x = R/6$. 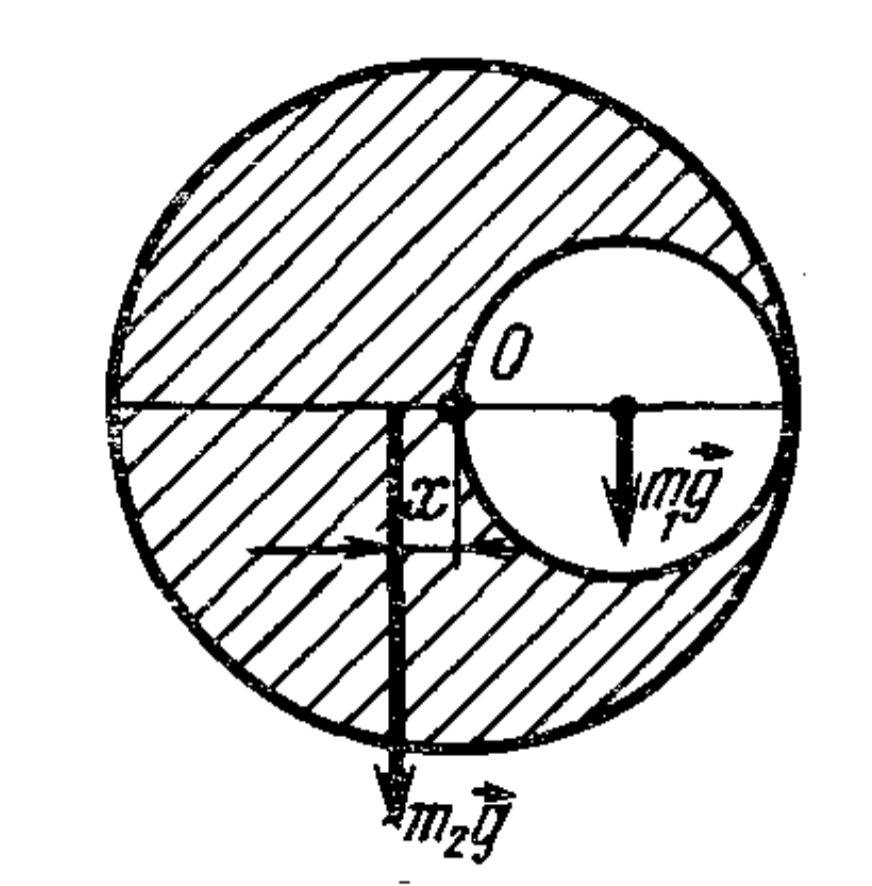
37. Where is the center of gravity of a cube from which a small cube with edge $a/2$ has been removed (see figure)? 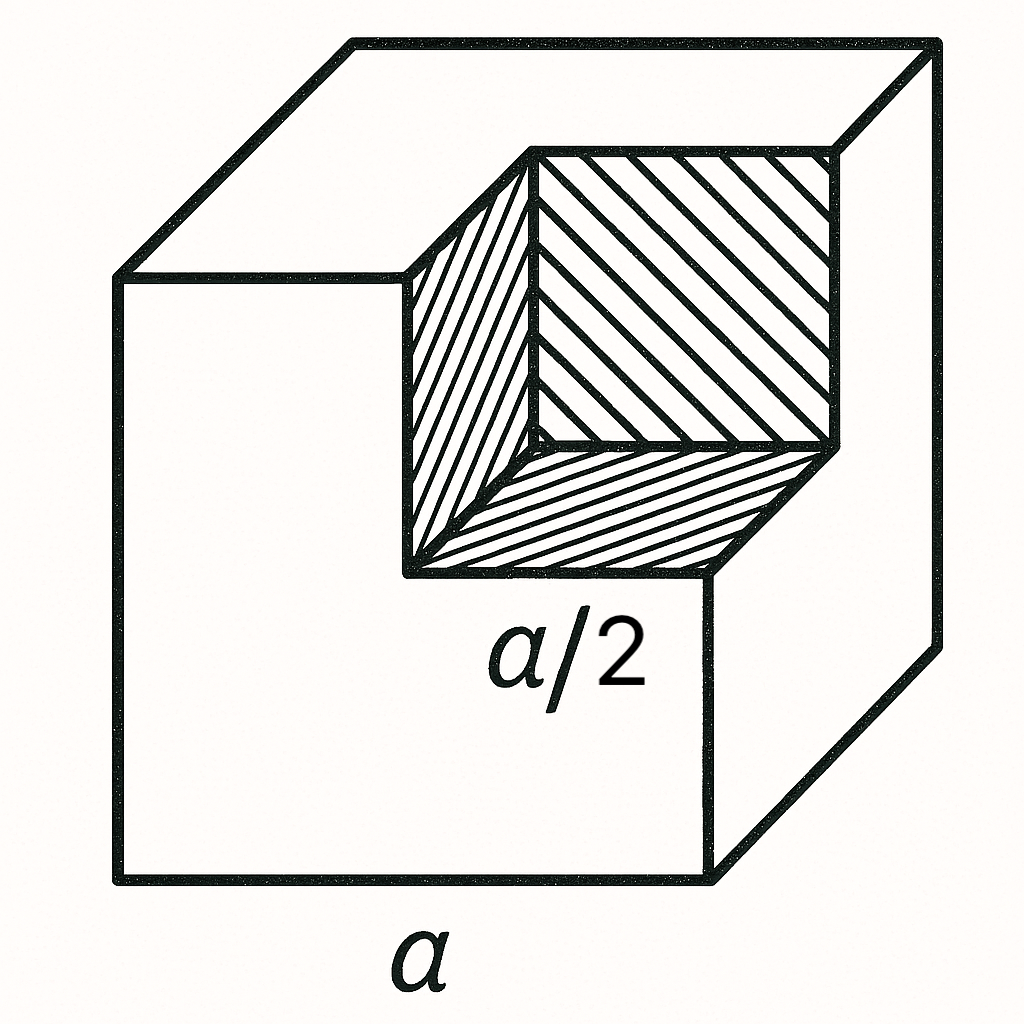
Answer
$a\sqrt{3}/28$ from the geometric center of the cube.
Hint
See the solution to the previous problem.
38. A rod of length $l = 15$ cm and mass $m = 0.025$ kg is placed in a tall, smooth cylindrical glass of radius $R = 6$ cm. What are the forces the rod exerts on the bottom and the wall of the glass? Neglect friction.
Answer
Horizontal forces are equal to $mgR/\sqrt{l^2 - 4R^2} \approx 0.16$ N. Vertical force is $mg \approx 0.25$ N.
39. Two identical spheres of radius $r$ and mass $m$ are placed in a hollow vertical cylinder open on both sides, with radius $R$ where $r > R/2$. The system is on a horizontal surface. What is the minimum mass $M$ of the hollow cylinder to prevent the spheres from toppling it?
Answer
$M \ge 2m(1 - r/R)$.
Solution
The cylinder will not tip over if the moment of its weight $Q$ relative to point $O$ (see figure) is not less than the tipping moment of forces $\vec{F}_1$ and $\vec{F}_2$ of the balls' pressure on the cylinder: $F_1 AO - F_2 B_1 O \le MgR\quad (Mg = Q).\tag{1}$ These forces, according to Newton's third law, are equal in magnitude to the forces $\vec{N}_1$ and $\vec{N}_2$ acting on the balls. On the upper ball, besides force $\vec{F}_1$, act the weight $m\vec{g}$ and the reaction force of the lower ball $\vec{N}_1$, directed along the line of centers. The forces acting on the lower ball are shown in the figure. From the equilibrium condition of the balls, we find that $F_1 = F_2 = mg \tan \alpha.$ Substituting these values into inequality (1) and considering that $AO - B_1 O = 2(R-r) \cot \alpha$, we find that $Mg \ge 2mg(1 - r/R).$ 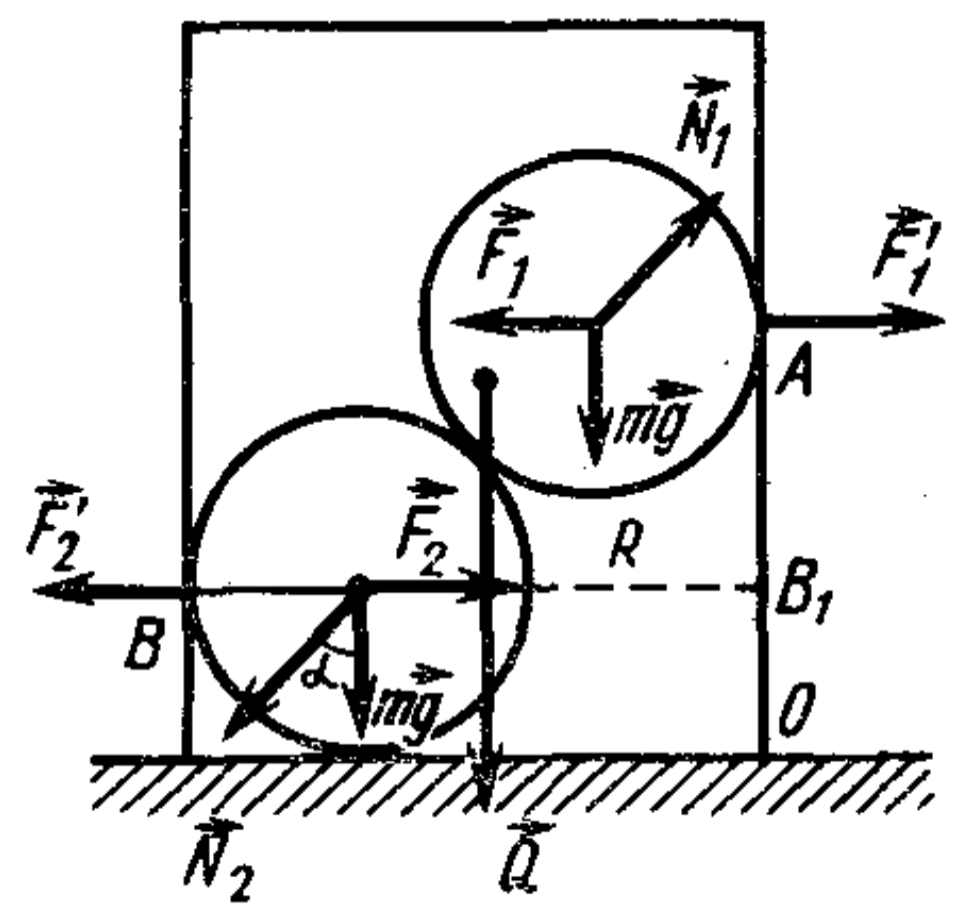
40. Two identical cylindrical logs lie side by side on the ground. A third identical log is placed on top. What is the minimum coefficient of friction $k$ between them so that they don’t roll apart (assuming no sliding on the ground)?
Answer
$k \ge 1/(2+\sqrt{3})$.
Hint
The logs will be in equilibrium if the moment of the pressure force from the upper log on each of the lower logs does not exceed the moment of the friction force of the upper log with the corresponding lower log relative to the line of contact of the log with the ground.
41. A round hole of radius $R/2$ is drilled parallel to the axis of a cylinder at a distance $R/2$ from its center. The cylinder lies on a board that is slowly lifted from one end (see figure). Find the limiting angle $\alpha$ at which the cylinder remains in equilibrium. The friction coefficient is $k = 0.2$. 
Answer
The cylinder will roll down at an angle of inclination of the plank $\alpha = \arcsin(1/6)$.
Solution
The center of mass of the cylinder with the hole (point O) is located at a distance $r = R/6$ from the axis of the cylinder (see problem 36). When the plank is tilted, the cylinder rotates so that its center of mass is on the vertical line passing through the point of contact of the cylinder with the plank. However, if this vertical line passes from the axis of the cylinder at a distance greater than $r=R/6$ (see the following figure), equilibrium is impossible. This means that the cylinder will start rolling when the angle $\alpha$ is such that $\sin \alpha_1 = r/R = (1/6)R/R = 1/6;\quad \alpha_1 = \arcsin(1/6).$ At the same time, the cylinder will start sliding at such an angle of inclination of the plank at which $\tan \alpha_2 = k = 1/5,$ hence $\alpha_2 = \arctan(1/5)$; $\alpha_1 < \alpha_2$, therefore rolling will occur before sliding. 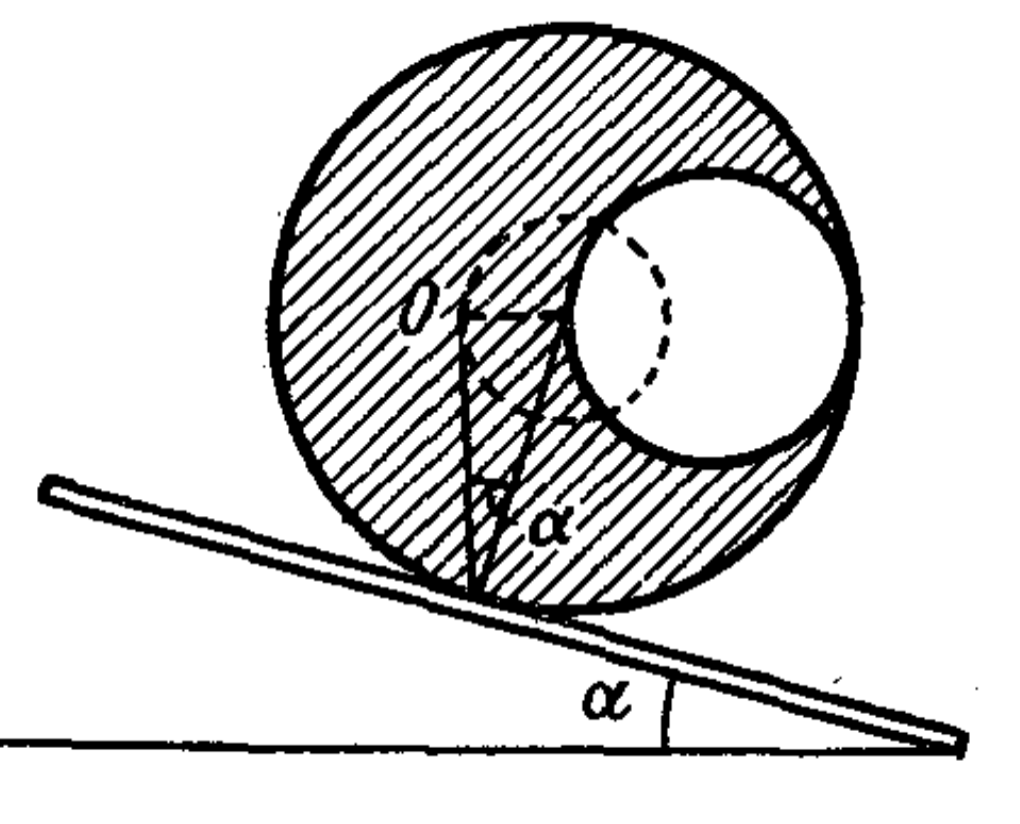
42. A hemisphere and a cylinder of the same radius made of the same material are joined as shown in the following figure. The system rests on a horizontal surface. For what height $x$ of the cylinder will the system be in neutral equilibrium? The center of gravity of the hemisphere lies on the axis, offset by $3/8$ of the radius from its center. 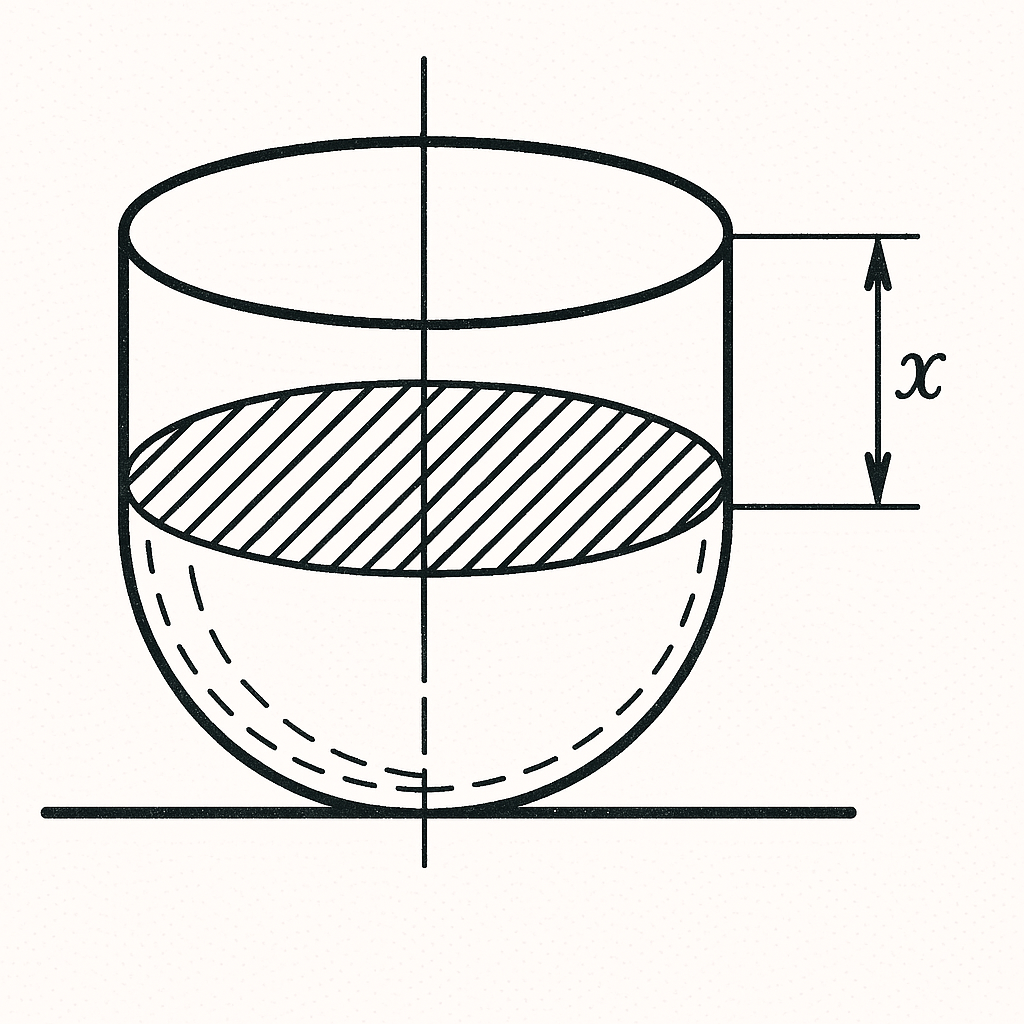
Answer
$x = R/\sqrt{2}$.
Hint
The system is in indifferent equilibrium if its center of gravity coincides with the geometric center of the hemisphere.
43. Water is poured into a cylindrical glass. At what water level does the center of gravity of the glass with water reach its lowest point?
Answer
The center of gravity of the glass with water is in the lowest position when it coincides with the water level in the glass. (Explain!)
44. A heavy block is held by friction between two horizontal rods $A$ and $B$ (see figure). What must be the distance from the block’s center of gravity to its contact point with rod $A$ so it doesn’t slip out? The values of distance $a$, angle $\alpha$, and friction coefficient $k$ are given. 
Answer
$x \ge \frac{a}{2} (\frac{\tan \alpha}{k} - 1)$.
Solution
The block will not slide out if the component of the gravity force along the block does not exceed the maximum friction force (see figure): $mg \sin \alpha \le F_{fr.max} = N_A k + N_B k$. (1) The pressure forces $N_A$ and $N_B$ of the rods on the block are found from the condition that the sum of the moments of forces relative to points A and B is zero, respectively: $mg x \cos \alpha - N_B a = 0$; $mg(a-x)\cos \alpha - N_A a = 0$. Substituting the values of $N_A$ and $N_B$ found from here into inequality (1), we find that the block will not slide out if $x \ge \frac{a}{2} (\frac{\tan \alpha}{k} - 1)$. 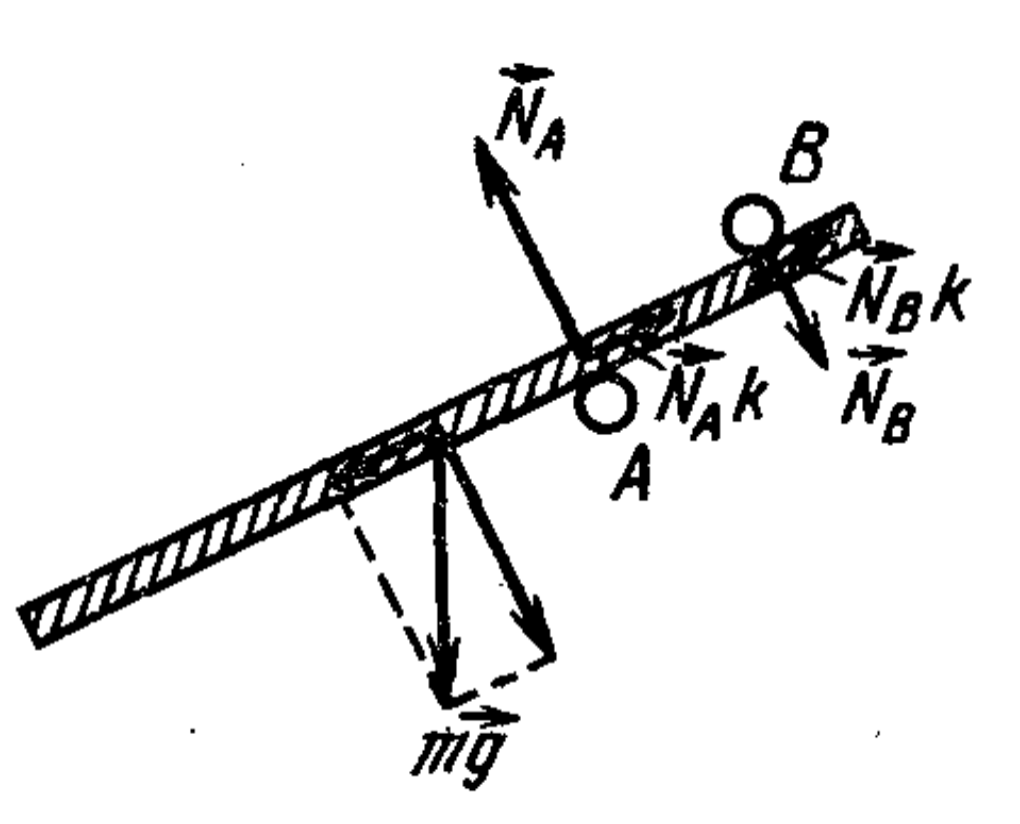
45. How much work is required to rotate onto a different face: a) a cube of mass 200 kg; b) a hollow cube half-filled with water? The cube’s mass is negligible compared to the water. Each edge is 1 m. Ignore gravitational work after the cube passes the point of unstable equilibrium.
Answer
a) 410 J; b) 1100 J.
Hint
The minimum work required to be done during infinitely slow tipping of the cube is equal to the difference in potential energies of the cube in the initial position and in the position of unstable equilibrium.
46. A cube-shaped box is moved a certain distance—once by dragging and once by tipping (i.e., rolling over its edge). For what value of the sliding friction coefficient $k$ is the work required equal in both cases?
Answer
$A_1 = mgka$; $A_2 = 0.207 mga$ for $k=0.207$ (see hint for problem 45).