Mechanical Oscillations and Waves
1. Write the equation of harmonic oscillation if the amplitude of the oscillation is 4 cm and the period is 0.01 s, given \( x_0 = 0 \).
Answer
$x = 4 \sin 200\pi t$.
2. During what fraction of the period \( T \) does a body performing harmonic oscillations travel the entire path from the mean position to the extreme position? The first half of the path? The second half?
Answer
$T/4$; $T/12$; $T/6$.
Solution
1st method. The following figure shows the graph of the displacement of the oscillating body versus time. At the initial moment, the displacement is zero. The phases in radians are marked on the abscissa axis. From the graph, it is clear that the entire path from the mean position to the extreme maximum displacement takes $T/4$ for the oscillating body. The oscillating body covers the first half of the path in $T/12$, which corresponds to the phase $\pi/6$ ($\sin(\pi/6) = 0.5$). The second half of the path is covered in time $T/4 - T/12 = T/6$.
2nd method. The displacement $x$ of the body is determined by the formula $x = a \sin(2\pi t / T)$, where $a$ is the amplitude, equal to the displacement to the extreme position; $t$ is the time counted from the moment of passing the equilibrium position. The time $t_1$ required for the body to travel from the mean position to the extreme position is determined from the condition $x = a$: $a = a \sin(2\pi t_1 / T)$, whence $2\pi t_1 / T = \pi/2$ and $t_1 = T/4$. The time $t_2$ required to travel the first half of this path is determined from the condition $x = a/2$, i.e., $a/2 = a \sin(2\pi t_2 / T)$, whence $2\pi t_2 / T = \pi/6$ and $t_2 = T/12$. The time $t_3$ to travel the second half of the path is $t_3 = t_1 - t_2 = T/6$.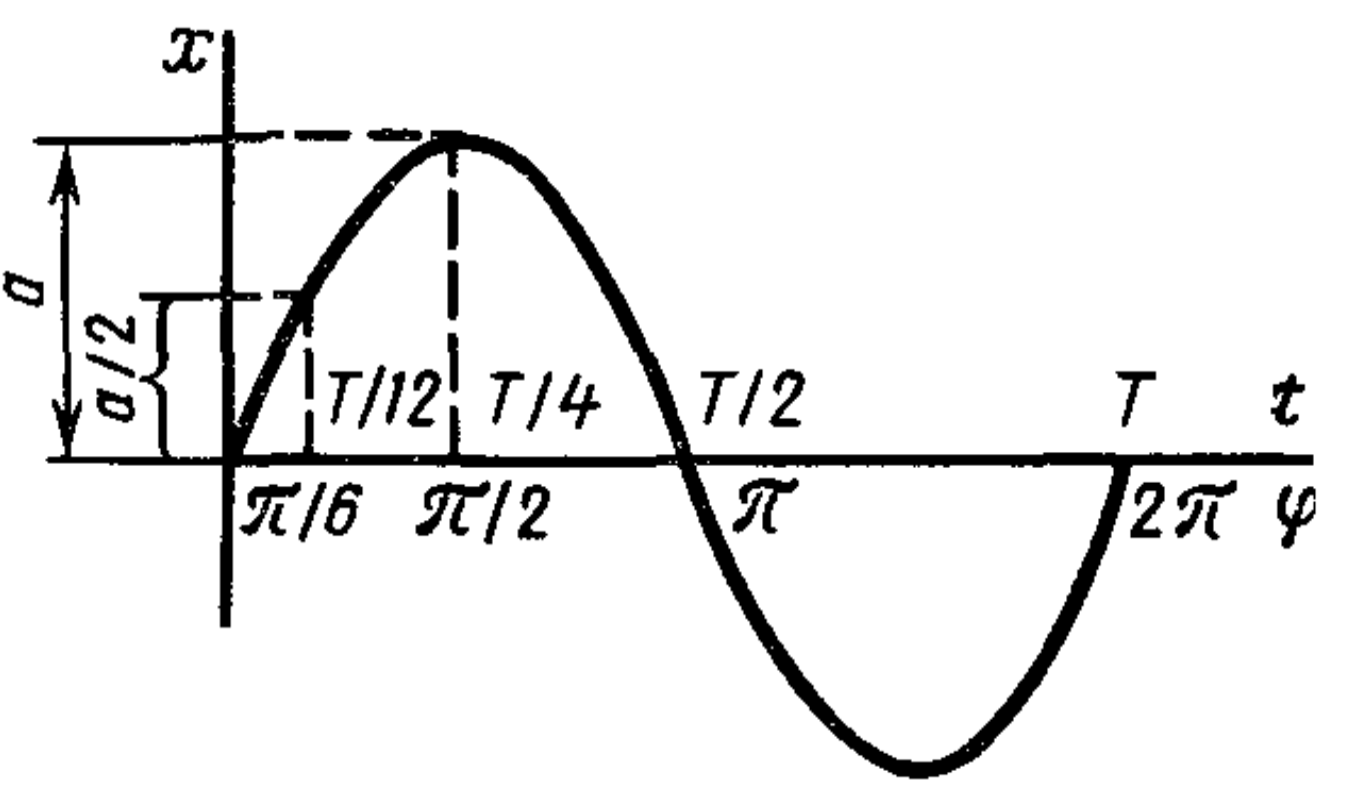
3. For what fraction of the period is the pendulum bob within 1 cm of the equilibrium position if the amplitude of its oscillations is 2 cm?
Answer
$T/3$.
Hint
See the solution to the previous problem.
4. Show that the period of motion of a conical pendulum (a mathematical pendulum moving in a circle) is equal to the period of its oscillations in a plane for small angles of deviation.
Solution
Circular motions of a 'conical' pendulum can be obtained if the deflected pendulum is given a push (velocity) in a direction perpendicular to the plane of possible oscillations after the initial deflection. Thus, 'conical' motions can be considered as the result of the superposition of two independent mutually perpendicular oscillations. The periods of these oscillations are the same (any plane of swing is no different from any other). Consequently, the period of the complex motion - the revolution of the pendulum along the cone - will be the same as the period of oscillation of a simple pendulum. The period of revolution of a 'conical' pendulum performing circular motion at small angles at the apex of the cone is $T = 2\pi \sqrt{l/g}$ (see problem 30 in Chapter: Circular Motion).
5. By what fraction of its length must a mathematical pendulum be shortened so that its period of oscillation at an altitude of 10 km equals its period on the Earth's surface? (Ignore the Earth's rotation.)
Answer
Approximately 0.3% longer.
Hint
The condition for the equality of the periods of oscillation of pendulums of different lengths at different heights is expressed as follows: $l_0/g_0 = l/g_h$. Forming the derived proportion, we get $\frac{l_0 - l}{l_0} =\frac{g_0 - g_h}{g_0}.$ Considering that $g_h = \frac{\gamma M}{(R+h)^2} \approx g_0 (\frac{R}{R+2h})$ (see problem 5 in Chapter: Conservation of Energy), it is easy to find $\frac{l_0 - l}{l_0} \approx 2h/(R+2h) \approx 2h/R \approx 3 \times 10^{-3}.$
6. Determine how much a pendulum clock will lose in a day if it is raised to an altitude of 5 km above the Earth's surface. (Ignore the Earth's rotation.)
Answer
$\Delta t \approx 67.5$ s.
Solution
The period of oscillation of a pendulum at height $h$ is $T = 2\pi \sqrt{\frac{l}{g_h}}.$ The acceleration of gravity at this height is $g_h = g_0 (\frac{R}{R+h})^2,$ where $g_0$ is the acceleration at the Earth's surface and $R$ is its radius (see problem 5 in Chapter: Conservation of Energy). Then $T = 2\pi \sqrt{\frac{l}{g_h}} = 2\pi \sqrt{\frac{l}{g_0}} \left(\frac{R+h}{R}\right) = T_0 \frac{R+h}{R} = T_0 \left(1 + \frac{h}{R}\right),$ where $T_0$ is the period of oscillation at the Earth's surface. Thus, over time $T_0$, the clock lags by $\Delta T = T - T_0 = h\frac{T_0}{R}.$ Over time $t = 24$ h, the clock will lag by some time $\Delta t$, which relates to $t$ as $\Delta T$ relates to $T_0$, and obviously, $\Delta t / t = \Delta T / T_0$, whence $\Delta t = t \frac{\Delta T}{T_0} = t\frac{h}{R}.$
7. How can the change in the period of a pendulum placed above a spherical ore deposit with density \( \rho \) be used to estimate the volume of the deposit? The Earth's density is \( \rho_0 \) (\( \rho_0 > \rho \)).
Hint
For estimation, assume the deposit has the shape of a sphere of radius $r$. Then the force of gravity acting on a body of mass $m$ near the deposit should be less than far from it (on the Earth's surface) by the amount $\frac{\gamma m (\rho_0 - \rho) \cdot 4/3 \pi r^3}{r^2} = \frac{4}{3} \pi \gamma m (\rho_0 - \rho) r$. The acceleration $g'$ of free fall near the deposit will therefore be equal to $g - \frac{4}{3} \pi \gamma (\rho_0 - \rho) r$, and the period of oscillation of the pendulum $T' = 2\pi \sqrt{l/g'} = 2\pi \sqrt{l/g} \sqrt{g/g'} = T \sqrt{g/g'}$, where $T$ is the period of oscillation of the pendulum far from the deposit. Knowing $g'$, it is easy to find $r$.
8. Will the period of oscillation of a pendulum change if it is placed in water? Assume the pendulum has an ideally streamlined shape and that water friction is negligible.
Answer
The period of oscillation of the pendulum will increase.
Hint
The action of the buoyant force on the pendulum (Archimedes' force) reduces the tension force of the string, which is equivalent to a decrease in $g$.
9. A pendulum with a period \( T = 1 \, \text{s} \) hangs in a stationary elevator. With what acceleration is the elevator moving if the pendulum's period becomes \( T_1 = 1.1 \, \text{s} \)? In what direction is the elevator moving?
Answer
$a = g \left[1 - \left(\dfrac{T}{T_1}\right)^2\right] \approx 0.17g$. The acceleration is directed downwards. The direction of motion of the lift does not matter.
Soltuion
When the lift moves with constant acceleration $a$, the tension force of the pendulum string $F_N$ in its equilibrium position relative to the cabin is determined from Newton's second law: $ma = mg - F_N$, whence $F_N = m(g - a)$. In the last formula, $a$ is an algebraic quantity: positive when the lift's acceleration is directed downwards, and negative when the acceleration is directed upwards. It follows that when the pendulum is deflected, the force restoring it to the equilibrium position will be proportional not to $g$, but to $(g - a)$. This means that in the lift moving with acceleration $a$, a pendulum of length $l$ has a period $T_1 = 2\pi \sqrt{l/(g-a)}$. Taking the ratio of the periods of oscillation of the pendulum in the lift moving with acceleration and in a stationary lift and squaring it, we get $\left(\frac{T_1}{T}\right)^2 = \frac{g}{g-a},$ whence we find the answer: $a = g \times \left[1 - \left(\frac{T}{T_1}\right)^2\right] \approx 0.17g;$ the answer is positive, meaning the lift moves with acceleration directed downwards; the direction of velocity does not matter.
10. Find the period of oscillation \( T \) of a mathematical pendulum of length \( l \) suspended in a train car moving horizontally with acceleration \( a \).
Answer
$T = 2\pi \sqrt{l/\sqrt{g^2 + a^2}}$.
Hint
In the equilibrium position relative to the wagon, the tension force of the pendulum string $F_N$ will be equal to: $F_N = m\sqrt{g^2 + a^2}$.
11. Determine the wavelength \(\lambda \) of a sound wave in water produced by a source with a frequency of 200 Hz, given the speed of sound in water is 1450 m/s.
Answer
$\lambda = 7.25$ m.
12. Which tuning fork sounds longer: one clamped in a vise or one placed on a resonance box?
Answer
The tuning fork clamped in the vise sounds longer. The radiation of sound wave energy per unit time from the tuning fork standing on the resonator box is greater.
13. The speed of sound in water is 1450 m/s. What is the distance between the nearest points oscillating in opposite phases if the oscillation frequency is 725 Hz?
Answer
1 m.
14. At what speed \( v \) of a train will a pendulum of length \( l = 44 \, \text{cm} \) suspended in the train car oscillate most strongly, given the length of the rails is 25 m?
Answer
$v \approx 67.5$ km/h.
Hint
When the wagon wheels hit the rail joints, the wagon receives an impulse that has both vertical and horizontal components. If the period between impacts is equal to the period of oscillation of the pendulum, the latter will swing particularly strongly.
15. Waves propagate at a speed of 360 m/s with a frequency of 450 Hz. What is the phase difference between two points 20 cm apart?
Answer
$\pi/2$.
Hint
If two points are separated by a distance equal to $\lambda$, the phase difference is $2\pi$, and if by $l$, then $2\pi l / \lambda$.
16. A body is located at point \( A \) on the inner surface of a sphere. In which case will it reach the lowest point \( B \) faster: by sliding along the sphere's surface or along an inclined plane \( AB \)? Assume negligible friction, zero initial velocity, and that the distance \( AB \) is much smaller than the sphere's radius.
Answer
When moving along the surface of the sphere.
Solution
When moving along the surface of the sphere $t_1 = T/4 = \frac{1}{4} \cdot 2\pi \sqrt{\frac{R}{g}}$ ($T$ is the period of oscillation of a pendulum of length $R$. Explain!). When moving along the inclined plane $t_2 = \sqrt{\frac{2s}{a}} = \sqrt{2\frac{2R \sin \alpha} {g \sin \alpha}} = 2 \sqrt{\frac{R}{g}} > t_1$ ($\alpha$ is the angle of inclination of the plane).
17. A weight suspended from a spring causes it to elongate by \( \Delta l = 4 \, \text{cm} \). Find the period \( T \) of the spring's natural oscillations with the weight.
Answer
$T = 2\pi \sqrt{\Delta l / g} \approx 0.4$ s.
18. Find the period \( T \) of natural oscillations in the systems described in problem 14 in Chapter: Statics (see figure). 
Answer
For series connection of springs $T = 2\pi \sqrt{m\dfrac{k_1+k_2}{k_1 k_2}$. For parallel connection $T = 2\pi \times \sqrt{\dfrac{m}{k_1+k_2}}$.