Law of Universal Gravitation. Satellites. Weightlessness
1. Find the dimensions of the gravitational constant $G$ in SI units. Using its value and the acceleration due to gravity, determine Earth's mass M. Earth's radius $R \approx 6400$ km.
Answer
[$G$] = m$^3$/(kg$\cdot$s$^2$); $M \approx 6 \times 10^{24}$ kg.
Hint
Near the Earth's surface, the force of gravity imparts acceleration $g$ to bodies; $mg = G mM/R^2$, whence $M = gR^2/G$, where $R$ is the radius of the Earth.
2. Calculate the gravitational force between two touching lead spheres (diameter 1 m each). Lead density $11.3 \, \text{g/cm}^3$.
Answer
$F \approx 2.34 \times 10^{-3}$ N.
3. A lead sphere (radius $R$) contains a spherical cavity that touches its surface and passes through its center. Total mass $M$. Using the law of gravitation, find the force on a small mass $m$ placed at distance $d > R$ from the sphere's center along the line connecting centers of the sphere and cavity (on the cavity side).
Answer
$F = \frac{1}{7} G Mm \left[\dfrac{8}{d^2} - \dfrac{1}{(d-R)^2}\right]$.
Hint
The sought force is found as the difference between the forces that would act on the small sphere from the entire lead sphere and from the part that was removed from the sphere.
4. At what distance from Earth's surface is gravitational acceleration $1 \, \text{m/s}^2$?
Answer
$h \approx 13600$ km.
5. Determine gravitational acceleration $g$ at height $h = 20$ km above Earth, given surface gravity $g_0 = 981 \, \text{cm/s}^2$ and Earth radius $R = 6400$ km.
Answer
$g \approx 975$ cm/s$^2$.
Solution
The acceleration due to gravity is found from the formulas $g_0 = G \frac{M}{R^2}$ and $g = G \frac{M}{(R+h)^2}$. Hence $\frac{g_0}{g} = (\frac{R+h}{R})^2 = 1 + \frac{2h}{R} + \frac{h^2}{R^2} \approx 1 + \frac{2h}{R},$ since $h/R \ll 1$, and therefore $h^2/R^2 \ll 2h/R$. Thus, $g = g_0 \times (\frac{R}{R+h})^2 \approx \frac{g_0 R}{R+2h}.$
6. Prove that gravitational force on a mass $m$ inside Earth is $F = mgr/R_0$, where $r$ is distance from center and $R_0$ is Earth's radius. Assume constant Earth density.
Answer
Hint. Let's show that the gravitational force acting from an arbitrary spherical shell on a material point inside it is zero. For this, let's divide the spherical shell into thin spherical layers. A cone with a small solid angle with its vertex at this point cuts out elements from the layer, and it can be shown that $\Delta m_1 / (\Delta m_2) = r_1^2 / r_2^2.$ Therefore, the resultant gravitational forces towards these elements are equal to zero. Dividing the entire layer into such elements, we obtain the initial statement. Consequently, only the mass of that part of the Earth enclosed within the sphere of radius $r$ acts on the point.
7. A body falls through a straight shaft drilled along Earth's rotation axis. Find its maximum velocity (ignore air resistance).
Answer
$v = \sqrt{gR}$.
Solution
If the mass of the body falling through the shaft is $m$, then the acceleration $a$ of the body depends on the distance $r$ to the center of the Earth according to the law $a =\frac{F}{m} = \frac{mgr/R}{m} = g \frac{r}{R}$ where $R$ is the radius of the Earth (see problem 6).
The acceleration is maximum at $r = R$ and becomes zero at $r = 0$. This means that the speed of the body is maximum at $r = 0$. After the body passes the center of the Earth, its acceleration is directed opposite to the velocity, and the speed of the body will decrease. To find the speed of the body at $r = 0$, let's use the law of conservation of energy. Assuming that the potential energy of the body is zero at the center of the Earth, we get $mv^2/2 = \Pi$, where $\Pi$ is the potential energy of the body on the surface of the Earth. It is equal to the work that must be done to very slowly move the body from the center to the surface of the Earth. Let's plot the graph of the dependence of the force that needs to be applied to the body on the distance $r$ (see figure). The work done in moving the body is numerically equal to the area of the shaded triangle (see problems 5 and 17 in Chapter: Work, Power, Energy ), therefore
$\Pi = mgR/2\ \text{ and }\ mv^2/2 = mgR/2.$
Hence
$v = \sqrt{gR}.$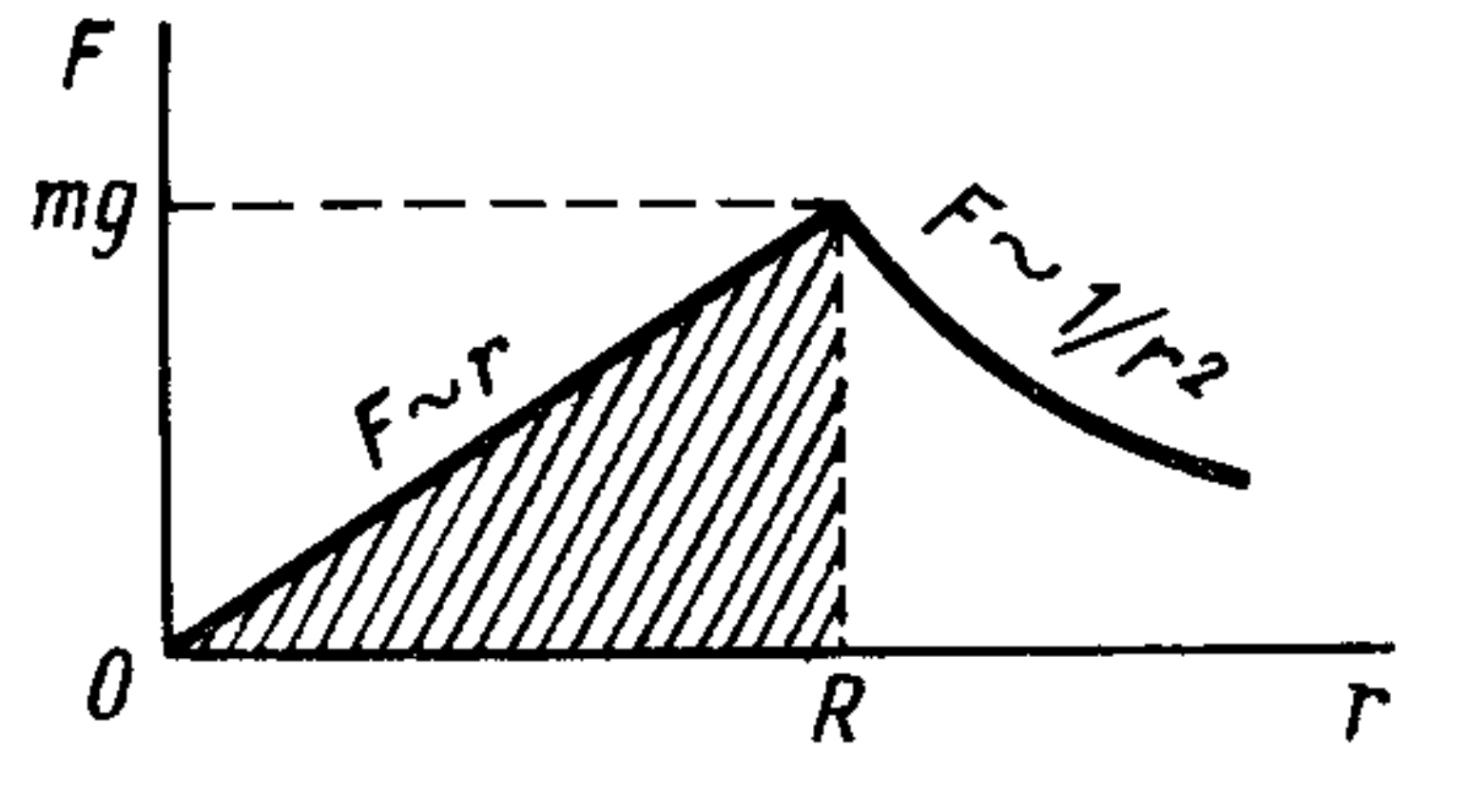
8. What direction and horizontal speed must an airplane fly along the equator to compensate for reduced weight due to Earth's rotation?
Answer
In the direction from east to west with a speed $v = 464$ m/s.
Hint
The aircraft must be stationary in the coordinate system associated with the fixed stars. For this, the angular velocity of the aircraft must be equal to the angular velocity of the Earth and directed in the opposite direction. When flying over the equator $v = \omega R_E = 2\pi R_E / T,$ where $R_E$ is the radius of the Earth; $T$ is its period of rotation.
9. Why are space rockets typically launched west-to-east? Why are equatorial launches most advantageous?
Answer
The rotational speed of the Earth is used.
10. At a planet's equator, bodies weigh half as much as at poles. Planet density $ρ = 3 \times 10^3 \, \text{kg/m}^3$. Determine its rotation period.
Answer
$T = \sqrt{6\pi/(\rho G)} \approx 2$ h 41.6 min.
Solution
The weight $P$ of a body is the force with which the body acts on a suspension or support that is stationary relative to the body. According to Newton's third law, the support acts on the body with a force $P'$, equal and opposite to $P$. Thus, two forces are applied to bodies at rest on the planet: the force of gravity $F_g$ and the reaction force of the support $P'$. These forces impart the necessary centripetal acceleration to the body during the rotation of the planet around its axis. At the pole and the equator, these forces are directed along the same line. According to Newton's second law $\frac{mv^2}{R} = F_g - P',$ where $v$ is the speed of the rotational motion of the body together with the Earth around its axis. At the pole $v = 0$ and the centripetal acceleration is absent. The reaction force of the support and, consequently, the weight of the body at the pole are equal to the force of gravity: $P_0 = F_g.$ At the equator $v = \dfrac{2\pi R}{T}$, where $T$ is the period of revolution. The weight of the body at the equator $P_e = F_g - m \frac{4\pi^2 R}{T^2}.$ According to the condition, $P_e = 0.5 P_0 = 0.5 F_g,$ then $\frac{4\pi^2 m R}{T^2} = 0.5 F_g.\tag{1}$ According to the law of universal gravitation $F_g = G \frac{mM}{R^2}.$ Here $m$ is the mass of the body; $M$ is the mass of the planet; $R$ is the radius of the planet, but $M = \frac{4}{3} \pi R^3 \rho,$ where $\rho$ is the density of the planet. Substituting the expressions for $F_g$ and $M$ into formula (1), we get $0.5 G \frac{m \cdot 4/3 \pi R^3 \rho}{R^2} = \frac{4\pi^2 m R}{T^2}.$ After simplification, we find $T = \sqrt{6\pi/(\rho G)}.$
11. Find the average density of a planet where spring scales show 10% less weight at the equator than at poles. Day length $T = 24$ hours.
Answer
$\rho = 30\pi/(T^2G) \approx 180$ kg/m$^3$.
12. How long should an Earth day be for equatorial weightlessness?
Answer
$t \approx 1$ h 25 min.
Hint
See problem 10.
13. Derive the dependence of body weight on geographic latitude.
Solution
Two forces act on the weighed body: the force of gravity $F_g$, directed towards the center of the Earth, and the reaction force of the support $P'$ (see figure); $P'$ is numerically equal to the weight of the body. The resultant $Q$ of the forces $F_g$ and $P'$ imparts centripetal acceleration $a = \omega^2 r$ to the body. Since $r = R \cos \phi$ ($\phi$ is the geographical latitude), then $a = \omega^2 R \cos \phi\quad\text{and}\quad Q = m\omega^2 R \cos \phi$ where $m$ is the mass of the body. In turn, for the force of gravity $F_g$, we can write $F_g = G mM/R^2 = mg_0,$ where $g_0 = G M/R^2$ ($M$ is the mass of the Earth) is a coefficient with the dimension of acceleration, numerically close to the acceleration of free fall at the pole. According to the cosine theorem from the triangle of forces, we get $P' = \sqrt{F_g^2 + Q^2 - 2F_g Q \cos \phi} = F_g \sqrt{1 + (\frac{Q}{F_g})^2 - \frac{2Q}{F_g} \cos \phi}.$ Considering that $Q/F_g \ll 1$, we can neglect the square of this quantity in the radicand. Using the known approximation $\sqrt{1 - \alpha} \approx 1 - \alpha/2$ for $\alpha \ll 1$, we obtain the final expression: $P' \approx F_g (1 - \frac{Q}{F_g} \cos \phi) = m(g_0 - \omega^2 R \cos^2 \phi)$. 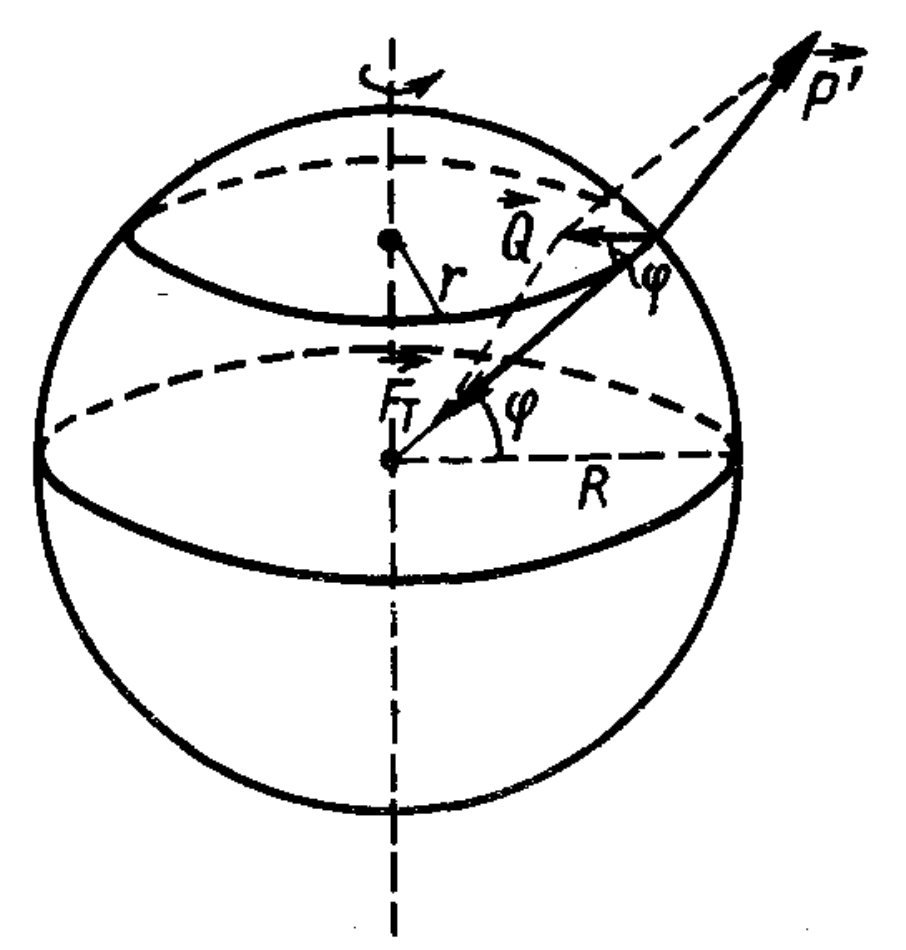
14. Calculate the Sun-Earth mass ratio given: Moon completes 13 orbits/year; average Sun-Earth distance is 390× greater than Moon-Earth distance.
Answer
336,000 times.
Solution
The equations of motion of the Earth around the Sun and the Moon around the Earth will be: $G \frac{m_E M_S}{R_{ES}^2} = m_E \omega_E^2 R_{ES};$ $G \frac{m_M m_E}{R_{ME}^2} = m_M \omega_M^2 R_{ME},$ or $G \frac{M_S}{R_{ES}^3} = \omega_E^2;$ $G \frac{m_E}{R_{ME}^3} = \omega_M^2.$ Dividing the first equation by the second and considering that $\omega = 2\pi/T$, we find $\frac{M_S}{m_E} = \frac{R_{ES}^3}{R_{ME}^3} \frac{T_M^2}{T_E^2}.$
15. Determine the Sun's mass using gravitational constant γ, Earth's orbital period $T$, and Earth-Sun distance $L = 1.5 \times 10^{11}$ m.
Answer
$m_S \approx 2 \times 10^{30}$ kg.
Hint
See problem 14.
16. Can a satellite orbit in a plane not passing through Earth's center?
Answer
No. Because in this case, the force of gravity would have a component not lying in the plane of the orbit.
17. A satellite orbits Earth at height $h$ (Earth radius $R$). For circular orbit, express orbital velocity and period in terms of $h$, $R$, and surface gravity $g$.
Answer
$v = R\sqrt{\dfrac{g}{R+h}$; $T = 2\pi \dfrac{R+h}{R} \sqrt{\dfrac{R+h}{g}}$.
Solution
Assume that the satellite moves in a circular orbit, the center of which is at the center of the Earth. In this case, the satellite moves with centripetal acceleration $a_{\text{cp}} = \frac{v^2}{R+h},$ where $v$ is the speed of the satellite in orbit; $R$ is the average radius of the Earth; $h$ is the average altitude of the satellite. This centripetal acceleration is provided to the satellite by the force of gravity $F = G \frac{mM}{(R+h)^2},$ where $M$ is the mass of the Earth; $m$ is the mass of the satellite; $G$ is the gravitational constant. According to Newton's second law, we have $\frac{m\,v^2}{R+h} = G \frac{mM}{(R+h)^2},$ whence $v^2 = G \frac{M}{R+h}.$ The value $G M$ can be found from the following relation: the weight of the body on the surface of the Earth $mg = G \frac{mM}{R^2},$ whence $G M = gR^2.$ Substituting the value $G M$ into the formula for the speed of the satellite, we get $v = R\sqrt{\frac{g}{R+h}}.$ The period of revolution of the satellite $T = 2\pi/\omega,$ where $\omega = v/(R+h)$ is the angular velocity of the satellite in orbit. Consequently, $T = \frac{2\pi(R+h)}{v} = 2\pi \frac{R+h}{R} \sqrt{\frac{R+h}{g}}.$
18. Find average angular $\omega$ and linear $v$ velocities of a satellite with 105-minute orbital period.
Answer
$\omega = 2\pi/T \approx 0.001$ rad/s; $v = \sqrt[3]{2\pi g R_E^2 / T} \approx 7.4 \times 10^3$ m/s.
Solution
The radius of the orbit $R$ can be found from Newton's second law equation $mv^2/R = G \frac{Mm}{R^2}.$ Expressing the linear velocity $v$ in terms of the angular velocity $\omega$, we get $v = \omega R$. Using the relation $G M = gR_E^2$ (see problem 17), we obtain $R = \sqrt[3]{\frac{gR_E^2}{\omega^2}},$ and further, $v = \omega R = \sqrt[3]{gR_E^2 \omega} = \sqrt[3]{2\pi g R_E^2 / T}.$
19. What orbital radius and velocity would give a satellite Earth's rotation period? What trajectory would it appear to have from Earth? What orbital plane would make it appear stationary?
Answer
$R = \sqrt[3]{gR_E^2/\omega^2} \approx 42000$ km; $v = \sqrt[3]{gR_E^2 \omega} \approx 3.1$ km/h.
Hint
See the previous problem. The angular velocity of rotation of the satellite must be equal to the angular velocity $\omega$ of the Earth's rotation. From the Earth, it will seem that the satellite moves forward and backward along the meridian. It will appear stationary if its orbit lies in the plane of the equator.
20. What is the first cosmic velocity for a planet with twice Earth's mass and radius?
Answer
$v_1 \approx 8$ km/s, the same as Earth's.
Hint
The first cosmic velocity is the speed of a satellite moving in a circular orbit around a planet near its surface. Therefore $mv_1^2/R = G mM/R^2,$ whence $v_1 = \sqrt{\frac{G M}{R}}.$ Since $M/R = M_E/R_E$, and $G M_E = gR_E^2$, we get $v_1 = \sqrt{gR_E}.$
21. What is the first cosmic velocity for a planet with Earth's density but half its radius?
Answer
$v_1 \approx 4$ km/s, i.e., half that of Earth.
22. A satellite required $A = 3.2 \times 10^{10}$ J work to reach low circular orbit. Find its mass (Earth radius $R_3 = 6400$ km).
Answer
1000 kg.
Solution
Neglecting the change in the potential energy of the satellite, we can write $A = mv^2/2$. To move in an orbit with radius $R \approx R_E$, the satellite must have a speed $v = \sqrt{gR_E}$ (see problem 17), then $A = mgR_E/2.$ Hence $m = 2A/(gR_E).$
23. Compare energy costs for: a) lifting a satellite to $h_1 = 3200$ km vs. orbital insertion at that height; b) same for $h_2 = 6400$ km.
Answer
In the first case 1:1, in the second 2:1.
Solution
If the potential energy of a body of mass $m$ in the gravitational field is considered zero infinitely far from the Earth (mass $M$), then at a distance $R$ from the center of the Earth it should be equal to $-G Mm/R$ (this formula can be easily obtained based on the analogy of gravitational and electrostatic fields or by considering the work done when moving the body over a small segment $\Delta R$). To lift the satellite to a height $h$ above the Earth's surface, work must be done equal to the change in the potential energy of the satellite: $A = \Pi_{R_E+h} - \Pi_{R_E} = -G \frac{Mm}{R_E+h} - (-G \frac{Mm}{R_E}) = mg \frac{hR_E}{R_E+h}$ (since $G M/R_E^2 = g$). To launch the satellite at this altitude, it needs to be given kinetic energy $mv^2/2$, i.e., perform work $A_1 = mv^2/2.$ For the satellite to rotate in orbit at height $h$ from the Earth, it needs to be given a speed $v = R_E \sqrt{g/(R_E+h)}$ (see problem 17), then $A_1 = \frac{1}{2} \frac{mgR_E^2}{R_E+h}.$ The ratio of the works is $A/A_1 = 2h/R_E.$ For $h = 3200$ km $A/A_1 = 1$, for $h = 6400$ km $A/A_1 = 2$.
24. When would an astronaut experience weightlessness during interplanetary flight?
Answer
The astronaut will be in a state of weightlessness from the moment the spacecraft engines are turned off in outer space.
Solution
Let us consider the forces acting on the spacecraft and on the bodies located within it. The spacecraft and the bodies within it always move with the same acceleration. This acceleration for the spacecraft is determined by the thrust force $\vec{F}_T$, the drag force $\vec{F}_d$, and the resultant gravitational force $\vec{F}_g$, which is proportional to its mass $M$. For any body inside the spacecraft, the acceleration is determined by the normal force $\vec{N}$ (equal in magnitude to the force exerted on the support) and the resultant gravitational force $\vec{F}'_g$, which is proportional to the body's mass $m$: $ \vec{a} = \frac{\vec{F}_T + \vec{F}_d + \vec{F}_g}{M} = \frac{\vec{N} + \vec{F}'_g}{m} $ However, the gravitational force per unit mass (the gravitational field) is the same for both the spacecraft and the body: $ \frac{\vec{F}_g}{M} = \frac{\vec{F}'_g}{m} $ From this, it follows that: $ \vec{N} = \frac{m}{M}(\vec{F}_T + \vec{F}_d) $ Consequently, the force exerted by the body on the support (the "apparent weight" of the body) is: $ \vec{P} = -\vec{N} = -\frac{m}{M}(\vec{F}_T + \vec{F}_d) $ This relationship is valid for any stage of the spacecraft's motion. It can also be used to determine the g-forces experienced by the cosmonaut during takeoff and during entry into the dense layers of the atmosphere. When the spacecraft enters outer space ($\vec{F}_d = 0$) and its engines are shut down ($\vec{F}_T = 0$), then $\vec{P} = 0$. That is, all bodies on the spacecraft are in a state of weightlessness and do not experience the interactions and internal stresses associated with weight.
25. How would the operation of pendulum clocks ('walkers') and spring (wrist) watches change inside an interplanetary spacecraft?
Answer
Pendulum clocks will stop after the rocket engine is turned off. The movement of the spacecraft will not affect the running of wristwatches.
26. How can body mass be measured under weightlessness conditions?
Answer
Many methods are possible, based on the application of Newton's second and third laws. For example:
- measure the ratio of the velocities acquired by bodies with known and unknown masses after burning the thread compressing a spring between the bodies;
- act on the body with a known force $F$ and measure the acceleration $a$ obtained by the body in this case, then $m = F/a$;
- measure the tension force of a pre-calibrated spring when rotating the body attached to this spring with a known constant angular velocity, etc.
27. Is it possible to create artificial gravity inside a spaceship?
Answer
Yes, by rotating the spacecraft or turning on the engines.
28. Does the potential energy of objects relative to Earth change when they move inside an orbiting satellite?
Answer
Yes. The force of gravity acts on bodies in a state of weightlessness (see problem 24). The change in potential energy is still given by the formula $\Delta \Pi = mg_h \Delta h,$ where $g_h$ is the acceleration due to gravity at the given altitude.
29. Do Pascal's and Archimedes' laws remain valid under weightlessness conditions?
Answer
Formally, both laws are applicable, but Archimedes' law loses its meaning, since both the body and the displaced liquid are weightless.
30. How would the linear and angular velocities of a satellite change under conditions of weak atmospheric drag? Assume a circular orbit.
Answer
The linear and angular velocities of the satellite will increase.
Hint
The total energy of the satellite is $E = \Pi + K.$ The potential energy of the satellite $\Pi = -G mM/r$ (see problem 23). We find the kinetic energy $K$ from the relation $\frac{mv^2}{r} = G \frac{mM}{r^2},\quad T = G \frac{mM}{2r}.$ Thus, the total energy $E = -G \frac{mM}{2r}.$ Under conditions of motion with weak friction, the work done against friction forces is produced at the expense of the total energy $E$ of the satellite; in this case, as seen from the last relation, $|E|$ must increase, which is possible if $r$ decreases, and consequently $v$ and $\omega$ (see problem 17) increase.
31. In which case does a spacecraft experience greater heating due to atmospheric friction: during launch or during re-entry? Explain why.
Answer
When falling to Earth. When launched, its speed in the denser layers of the atmosphere near the Earth's surface is low, while during descent it is high.