Hydrostatics
1. A hollow cube with edge length \( a \) is filled to the top with a liquid of density \( \rho \). Determine the forces acting on the faces of the cube.
Answer
On the bottom $\rho g a^3$, on the side face $(1/2) \rho g a^3$.
Hint
The pressure $p$ in a liquid at depth $h$ is $\rho g h$, i.e., it varies linearly with height (see figure). Therefore, the total pressure force on the entire side face of the cube is equal in magnitude to the average pressure (i.e., the pressure at depth $a/2$) multiplied by the area of the face. 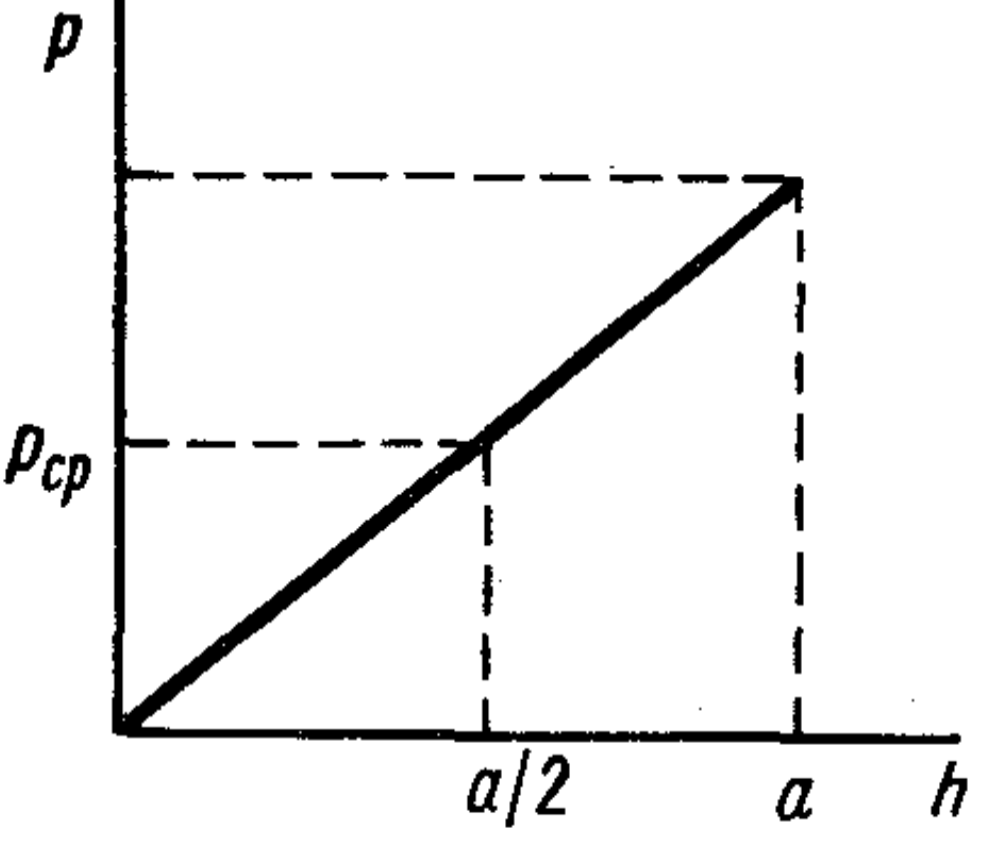
2. A vessel shaped like a truncated cone with a detachable bottom is submerged in water. If 200 g of water is poured into the vessel, the bottom detaches. Will the bottom detach if a 200 g weight is placed on it? If 200 g of oil is poured in? If 200 g of mercury is poured in?
Answer
If the container narrows upwards, the weight and mercury will not detach the bottom, but the oil will. If the container narrows downwards, the opposite is true.
Hint
The pressure force of the liquid acts on the bottom from the inside: $\rho g h S$ (where $\rho$ is density, $h$ is the liquid level height, $S$ is the bottom area). If the container narrows upwards, this force is greater than the weight of the liquid poured into the cone by the amount of the weight of the liquid occupying the shaded volume (figure, a). Therefore, mercury and the weight will not detach the bottom. Oil will detach the bottom, because in the case of a cone narrowing upwards, the product $ph$ for oil is greater than for water (oil will occupy a larger volume than the same amount of water. This relative increase in level height $h$ is greater than the relative decrease in density $\rho$). If the container narrows downwards, the pressure force of the liquid poured into the container on the bottom is less than its weight by the amount of the weight of the liquid in the shaded volume (figure, b). Therefore, in this case, oil will not detach the bottom, but the weight and mercury will. 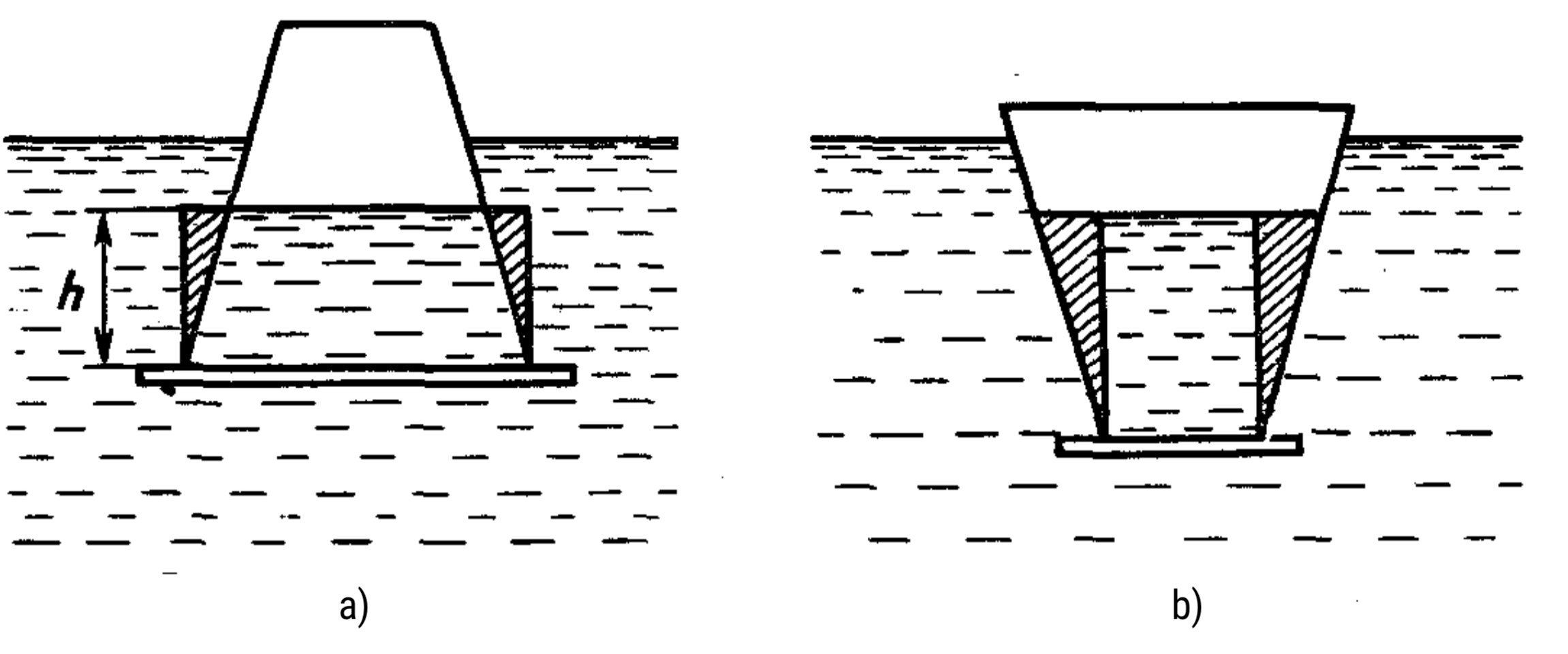
3. A tube with cross-sectional area \( S = 2 \, \text{cm}^2 \) is inserted into a vessel with water. Then, 72 g of oil (\( \rho_M = 900 \, \text{kg/m}^3 \)) is poured into the tube. Find the difference in the levels of the oil and water.
Answer
$\Delta h = 4$ cm.
Hint
Apply the equilibrium condition for non-uniform liquids in communicating vessels.
4. To lift a load of mass \( m = 2 \, \text{t} \) using a hydraulic press, work \( A = 40 \, \text{J} \) is expended. The small piston makes \( n = 10 \) strokes, moving \( h = 10 \, \text{cm} \) per stroke. By what factor is the area of the large piston greater than that of the small piston, assuming the press's efficiency is 1?
Answer
$S_2/S_1 = n h m g / A \approx 500$ times.
5. Water is poured into communicating vessels with diameters \( D_1 \) and \( D_2 \). By how much will the water level change in the vessels if a piece of wood with mass \( m \) is placed in the first vessel? In the second vessel? The density of water is \( \rho_0 \).
Answer
The water levels in both cases rise by $\Delta h = \frac{m}{\frac{\pi}{4} (D_1^2 + D_2^2) \rho_0}$.
6. Water and alcohol, separated by mercury, are poured into the arms of a U-shaped tube. The mercury levels in both arms are equal. At a height of 24 cm from the mercury level, the arms are connected by a horizontal tube with a valve (see figure). Initially, the valve is closed. Determine the height of the alcohol column \( h_2 \) (\( \rho_c = 800 \, \text{kg/m}^3 \)) if the height of the water column \( h_1 = 32 \, \text{cm} \). What happens if the valve is opened? At what position of the tube will equilibrium be maintained when the valve is opened? 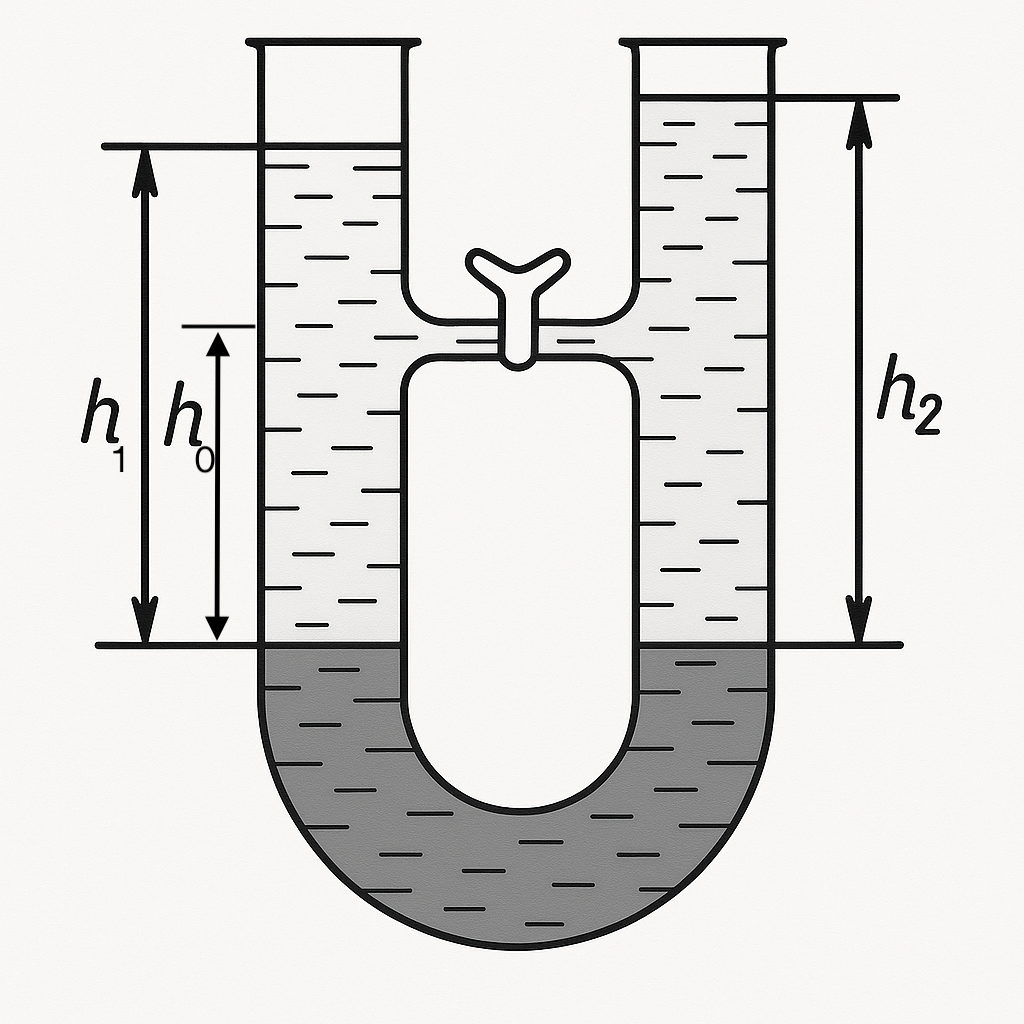
Answer
$h_2 = 40$ cm. Alcohol will flow over. The tube should be positioned inclined, descending towards the arm with water.
Hint
See problem 3. By plotting the graph of pressure versus height (initial level - mercury level) for both arms (see the following figure), it is easy to see that at the height where the tube is located, the pressure in the arm with alcohol is greater than in the arm with water. Therefore, alcohol will flow over. For equilibrium not to be disturbed when the tap is opened, the tube must be positioned inclined. The difference in heights of the tube connection points can be found using the graph. 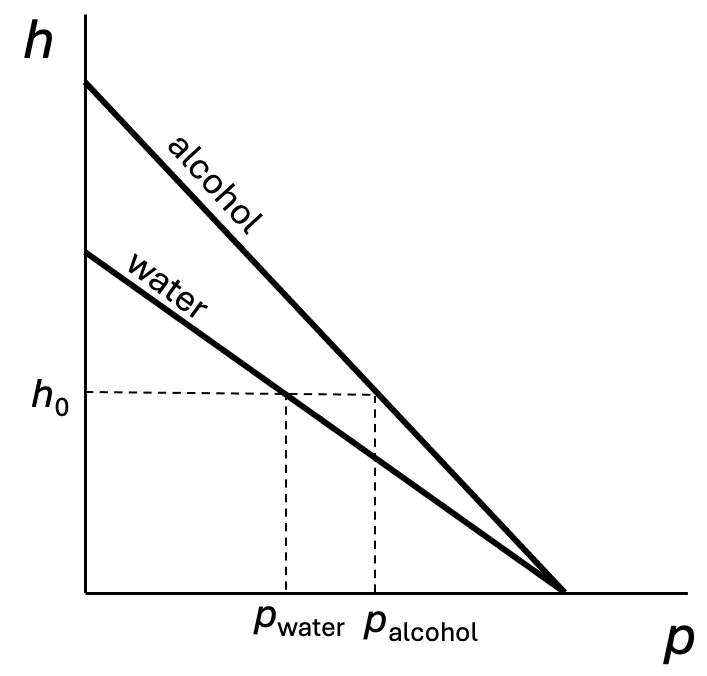
7. An ice floe with cross-sectional area \( S = 1 \, \text{m}^2 \) and height \( H = 0.4 \, \text{m} \) floats in water. What work must be done to fully submerge the ice floe in water?
Answer
$A = gSH^2 (\rho_w - \rho_i)^2 / (2\rho_w) \approx 7.84$ J.
Hint
During uniform immersion of the ice floe, the buoyant force $Q$ acting on it increases uniformly, and therefore the force $F = Q - mg = (\rho_w - \rho_i) gSh$ ($m$ is the mass of the ice floe, $\rho_w$ is the density of water, $\rho_i$ is the density of ice, $h$ is the depth of immersion) changes linearly with the immersion height from zero (when the ice floats) to the value $F_H = (\rho_w - \rho_i) gSH.$ Therefore, the work required to immerse the ice floe is equal in magnitude to the work of the average force $(1/2)F_H$ over the path equal to the thickness of the part of the ice floe protruding above the water.
8. A piece of ice floats in a glass of water. Will the water level change when the ice melts? Also consider the cases: 1) when the ice contains an air bubble; 2) when the ice contains a lead plate.
Answer
Ice displaces water whose weight is equal to the weight of the ice. When the ice melts, the same amount of water is formed, so the level will not change.
- The presence of an air bubble in the piece of ice does not change the previous reasoning (the mass of air is negligible), therefore, in this case too, the water level in the vessel will remain the same.
- If the ice contains a piece of lead, then the volume of water formed when the ice melts, together with the volume of the piece of lead, will be less than in the case of a piece of pure ice of the same weight. Consequently, the level will decrease.
9. One bottle is filled with water, the other with mercury. Will the water-filled bottle sink if placed in water? Will the mercury-filled bottle sink if placed in mercury?
Answer
The bottle with water will sink, but the one with mercury will not.
Hint
The weight of the bottle with water is greater than the weight of water whose volume is equal to the external volume of the bottle, while the bottle with mercury weighs less than the same volume of mercury.
10. A rectangular tin box with mass \( m = 76 \, \text{g} \), base area \( S = 38 \, \text{cm}^2 \), and height \( H = 6 \, \text{cm} \) floats in water. Determine the height \( h \) of the box's part above the water.
Answer
$h = H - m/(\rho_0 S) = 4$ cm, where $\rho_0$ is the density of water.
11. A 2-liter pot is completely filled with water. A body with volume \( 0.5 \, \text{L} \) and mass \( 0.6 \, \text{kg} \) is placed into the pot. How much water will spill out?
Answer
0.5 kg.
12. A tin can with a load floats on the surface of water in a vessel, with the water level at \( H_1 \). Will the new water level \( H_2 \) be higher or lower than \( H_1 \) if the load is moved from the can to the bottom of the vessel? The density of the load is greater than that of water.
Answer
Less.
Solution
When the weight is removed from the beaker, the volume of water displaced by the beaker will decrease by $V_1 = m/\rho_1$ ($m$ is the mass of the weight, $\rho_1$ is the density of water). When the weight is immersed in water, the volume of displaced water will increase by the volume of the weight $V_2 = m/\rho_2$ ($\rho_2$ is the density of the weight). Since $\rho_2 > \rho_1$, then $V_2 < V_1$, which means $H_2 < H_1$.
13. A liquid with density \( \rho \) is poured into a vessel with vertical walls and base area \( S \). By how much will the liquid level change if a body of arbitrary shape with mass \( m \) (which does not sink) is placed into the vessel?
Answer
$\Delta h = m/(\rho S)$.
Solution
1st method. When the body is placed in the vessel, the pressure force on the bottom increases by $\Delta F = mg.$ But the body itself does not touch the bottom of the vessel, so the pressure force changes due to the change in water pressure. If the water level in the vessel rises by $\Delta h$, then $\Delta p = \rho g \Delta h$ and $\Delta F = \rho g \Delta h S.$ Therefore $\rho g \Delta h S = mg$. Hence $\Delta h = m/(\rho S).$
2nd method. A body of mass $m$, floating on the surface of a liquid, according to Archimedes' law, will displace (occupy) a volume $\Delta V$ in it, which would be occupied by the same liquid of mass $m$. Thus, this immersion is equivalent (in the sense of changing the liquid level in the vessel) to adding liquid of mass $m$ to the vessel. Then $\Delta h = \Delta V / S = m / (\rho S)$.
14. A liquid with density \( \rho \) is poured into a U-shaped tube with cross-sectional area \( S \). By how much will the liquid level rise in the right arm relative to the initial level if a body with mass \( m \) and density \( \rho_1 < \rho \) is placed into the left arm?
Answer
$\Delta h = m/(2\rho S)$.
Hint
See problem 13. The changes in liquid levels in the arms are the same.
15. A mushroom-shaped concrete structure is installed at the bottom of a river (dimensions are given in the following figure). The river's depth is \( H \). With what force does the structure press on the riverbed? The density of concrete is \( \rho \), and that of water is \( \rho_0 \). 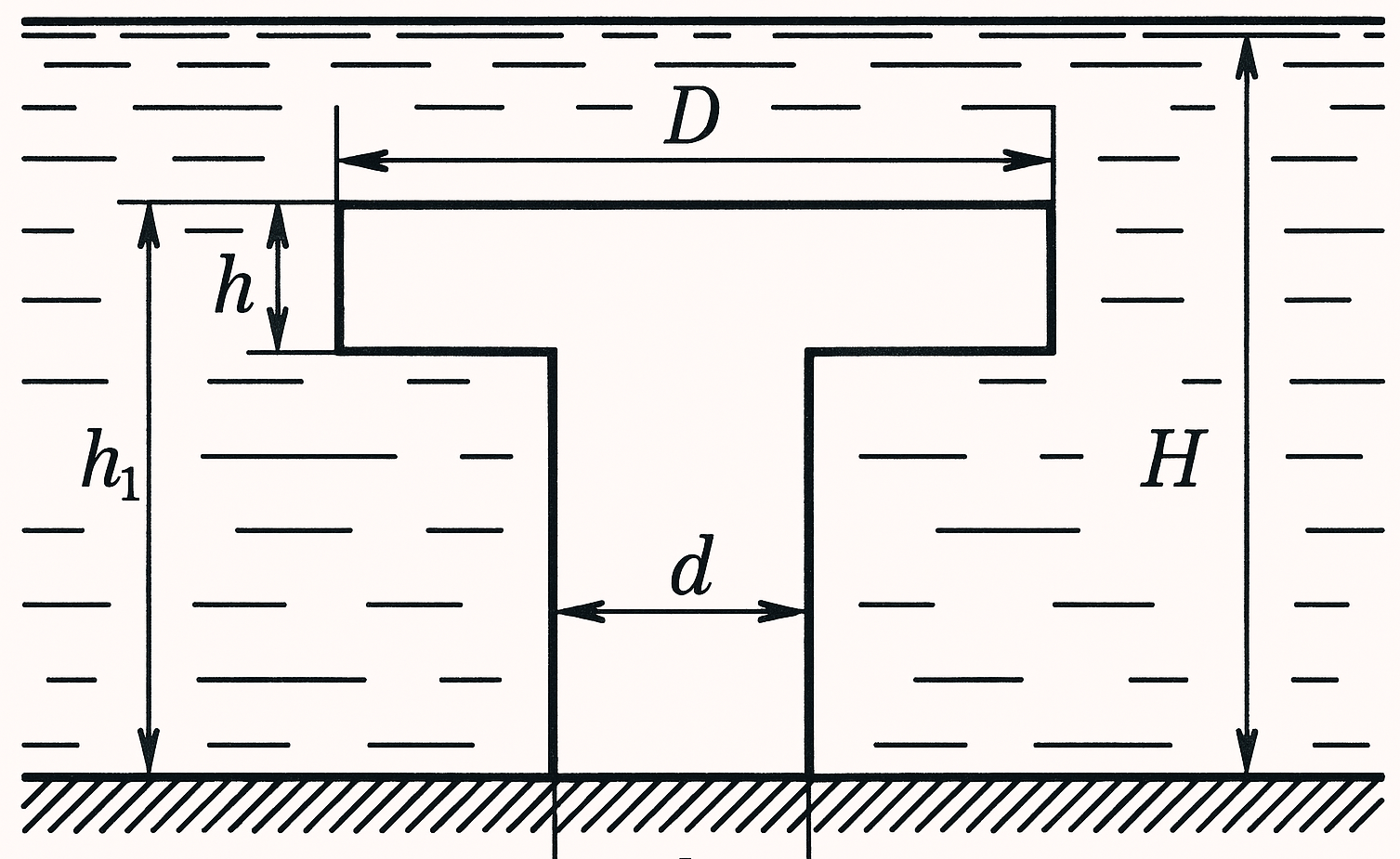
Answer
$g \frac{\pi}{4} \{ \rho_0 d^2 (H-h) + (\rho - \rho_0)(D^2 - d^2)h + \rho d^2 h_1 \}$.
Hint
The pressure force of the structure on the bottom consists of the pressure force of water on the upper surface of the part, the weight of the structure, and the pressure force of water on the lower surface, directed upwards and equal to $\frac{\pi}{4} (D^2 - d^2)[H - h_1 + h] \rho_0 g.$
16. A wooden cube lies at the bottom of a vessel. Will it float if water is poured into the vessel (assuming water does not seep under the cube)?
Answer
No, because the buoyant (Archimedean) force does not arise - hydrostatic pressure is not transmitted to the lower face of the cube due to the absence of liquid under it.
17. A round hole with area \( S_1 \) in the bottom of a vessel is loosely covered by a conical plug with base area \( S_2 \). What is the maximum density \( \rho \) of the plug material for which the plug can be made to float by adding water to the vessel? The density of water is \( \rho_0 \).
Answer
$p = p_0 \{ 1 + 2(S_1/S_2)^{1/2} - 3S_1/S_2 \}$.
Hint
The buoyant (Archimedean) force is maximum when the water reaches the top of the plug. At this point, it is equal to the weight of the water in the shaded volume of the plug (see the following figure). 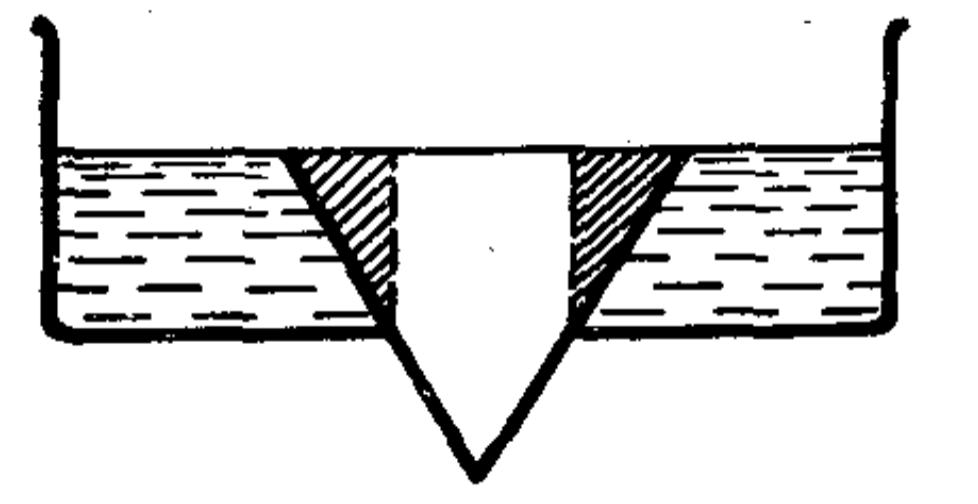
18. An empty open bottle is submerged neck-down into water to a depth \( h \) and released. The bottle neither rises nor sinks but remains in equilibrium. Why? Is this equilibrium stable? Determine the depth of submersion if the bottle's capacity is \( V_0 = 0.5 \, \text{L} \), its mass is \( m = 0.4 \, \text{kg} \), atmospheric pressure is \( p_0 = 101 \, \text{kPa} \), and the temperature is constant. Neglect the volume of the bottle's walls.
Answer
$h = p_0 (V_0 - m/\rho) / (mg) \approx 2.6$ m.
Hint
At the sought depth $h$, the water pressure is $p_1 = p_0 + \rho g h$, where $p_0$ is the air pressure above the water surface; $\rho$ is its density. For the air in the bottle, which compresses upon immersion, Boyle's law can be written: $p_0 V_0 = p_1 V_1,$ where $V_0$ and $V_1$ are the volumes of air in the bottle before and after immersion, respectively. Considering, finally, that the bottle at depth $h$ is in equilibrium, supported by the Archimedean force $mg = \rho V_1 g,$ we can obtain $p_1 = p_0 V_0 \rho / m.$
19. A hollow sphere (outer radius \( R_1 \), inner radius \( R_2 \)) made of material with density \( \rho_1 \) floats on the surface of a liquid with density \( \rho_2 \). What should be the density \( \rho \) of the substance filling the hollow part of the sphere for it to be in neutral equilibrium inside the liquid?
Answer
$\rho = R_1^3 (\rho_2 - \rho_1) + \dfrac{R_2^3 \rho_1}{R_1^3}$.
Hint
The sphere will be in suspension inside the liquid if its mass (weight) is equal to the mass (weight) of the liquid whose volume is equal to the volume of the sphere.
20. A hollow cast iron sphere floats in water, submerged exactly halfway. Find the volume \( V \) of the hollow part if the sphere's mass is \( m = 5000 \, \text{g} \) and the density of cast iron is \( \rho = 7.8 \, \text{g/cm}^3 \).
Answer
$V = m (\frac{1}{\rho} - \frac{1}{\rho_w}) \approx 9350 \text{ cm}^3$.
21. A vessel with water is balanced on a scale. How will the balance change if a block with dimensions \( 5 \times 3 \times 3 \, \text{cm}^3 \), suspended by a thread, is fully submerged into the water without touching the bottom? What weight and on which side must be added to restore balance?
Answer
45 g; on the other pan.
Hint
In accordance with Newton's third law, a force equal in magnitude to the Archimedean (buoyant) force acting on the block, and directed downwards, will act on the vessel with water from the side of the block. This force arises due to the increase in hydrostatic pressure on the bottom (and walls) of the vessel as a result of the rise in the water level in the vessel after immersing the block (see also problem 13).
22. Solid aluminum and iron balls are balanced on a lever. Will the balance be disturbed if the balls are submerged in water? Consider two cases: a) balls of equal mass; b) balls of equal volume.
Answer
In both cases, it will be disturbed; the iron ball will outweigh.
Hint
See the previous problem. In the second case, the arms are not equal and the moments of the buoyant forces are also not equal.
23. The weight of a piece of iron in water is \( P = 1.67 \, \text{N} \). Find its volume \( V_{\text{Fe}} \). The density of iron is \( \rho_{\text{Fe}} = 7.8 \, \text{g/cm}^3 \).
Answer
$V_x = 25.1 \text{ cm}^3$.
Solution
Since the weighed piece of iron is in equilibrium, we can write: $m_i g = P + m_w g$, where $m_i$ and $m_w$ are the masses of iron and water in volumes equal to $V_x$. The right side of the equality is the sum of the forces applied to the body: Archimedean force and the reaction force of the support (suspension), equal to the weight of the body in water $P$. Expressing the masses of iron and water through the volume $V_x$ and the corresponding densities, we get $V_x \rho_i g = P + V_x \rho_w g,$ whence $V_x = \frac{P/g}{\rho_i - \rho_w}.$
24. The weight of a body in water is three times less than its weight in air. What is the density of the body's material?
Answer
1.5 g/cm$^3$.
Solution
1st method. See the previous problem.
2nd method. Assume that the weight of the body in air is three units, then in water, according to the condition, the weight is one unit, i.e., the loss of weight in water is two units, which is equal to the weight of water in the volume of the body. Hence the density is $3/2$ g/cm$^3 = 1.5$ g/cm$^3$.
25. A wooden block floats in water. How will the depth of the block's submersion change if oil is poured on top of the water?
Answer
It will decrease, as the liquid pressure on the lower face of the block increases.
26. A certain body floats on the surface of water in a closed vessel. How will the depth of submersion change if air is pumped into the vessel?
Answer
It will not change if the compressibility of the body is the same as that of water; it will increase if the compressibility is greater than that of water, and decrease otherwise.
27. One end of a thread is fixed to the bottom, and the other is attached to a cork float. Here, 0.75 of the float's total volume is submerged in water. Determine the tension force \( F \) in the thread if the float's mass is 2 kg and the density of cork is \( 0.25 \, \text{g/cm}^3 \). Neglect the mass of the thread.
Answer
$F \approx 40$ N.
28. A bucket hangs from a dynamometer's hook. Will the dynamometer's reading change if the bucket is filled with water and submerged in water?
Answer
It will decrease by the amount of the weight of water displaced by the walls and bottom of the bucket.
29. A vessel, completely filled with water, hangs from a dynamometer. Will the dynamometer's reading change if a weight suspended by a thread is submerged into the water without touching the bottom?
Answer
The dynamometer reading will not change.
Hint
The water displaced by the weight will spill out of the vessel. Thus, the weight of the water in the vessel will decrease, which exactly compensates for the force arising from the weight on the vessel with water, which is equal to the buoyant (Archimedean) force acting on the weight. (See also problem 10.21).
30. A vessel with water and a stand with a copper weight of mass \( m = 100 \, \text{g} \) (see figure) are balanced on a lever scale. Then, the weight, suspended by a thread, is lowered into the water. How can the balance be restored? The density of copper is \( \rho_M = 8.9 \, \text{g/cm}^3 \). 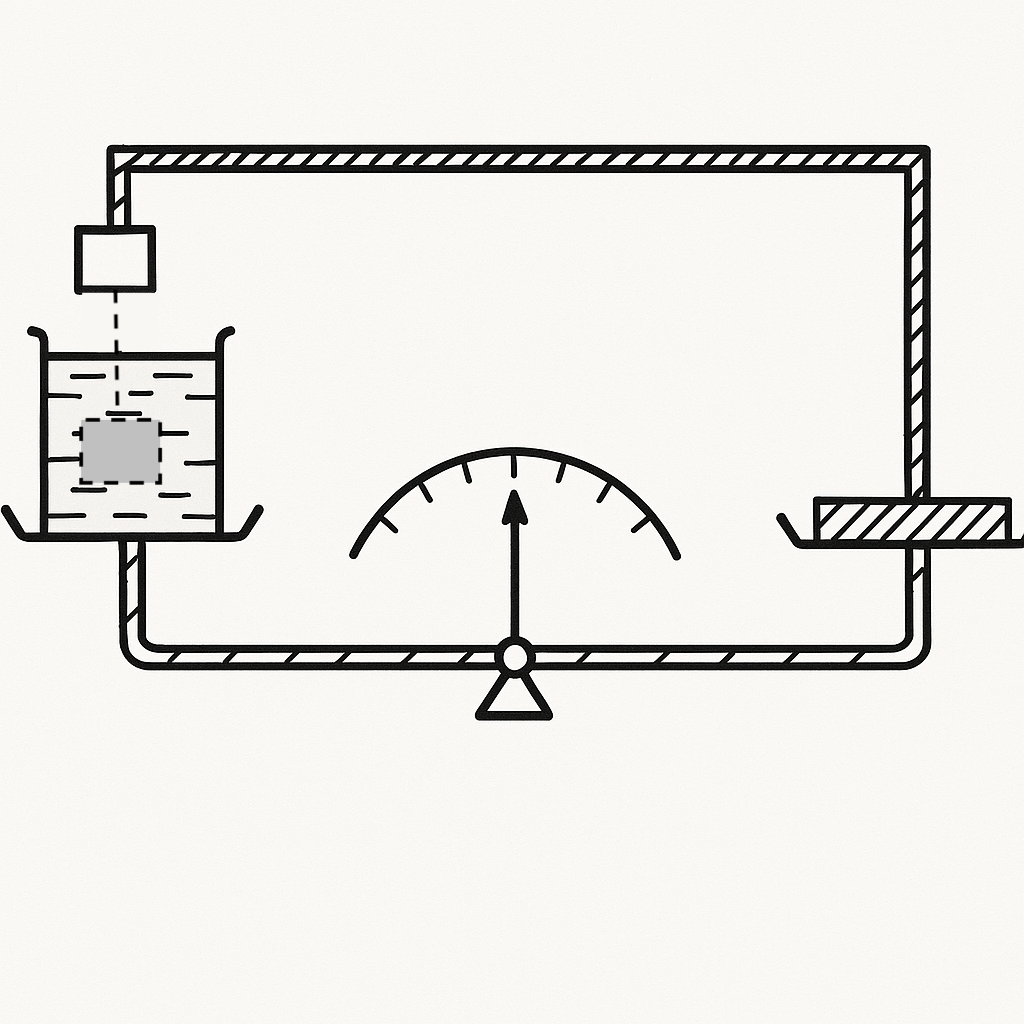
Answer
Place a weight of mass $M = 2m \rho_w / \rho_m \approx 24$ g on the right pan of the balance.
Hint
When the weight is immersed, the force acting on the left arm of the balance beam increases, and on the right - decreases by an amount equal to the buoyant force $F = V \rho_w g = m \rho_w g / \rho_m$ (see problem 10.21).
31. A thin uniform rod is hinged at its upper end. The lower part of the rod is submerged in water, and equilibrium is achieved when the rod is inclined to the water's surface, with half of it underwater. What is the density of the rod's material?
Answer
0.75 g/cm$^3$.
Solution
Since the stick is thin, we can assume that the buoyant force $Q$ is applied at the midpoint of the part of the stick submerged in water (see figure). By virtue of the equilibrium of the stick, the moments of forces $mg$ and $Q$ relative to point A must be equal, i.e., $mgx = Q \cdot (3/2)x$, whence $Q = (2/3)mg$. Substituting $m = \rho V$ and $Q = (1/2) \rho_w V g$ here ($V$ is the volume of the stick, $\rho$ is the density of the stick material and $\rho_w$ is the density of water), we find $\rho = (3/4) \rho_w$. 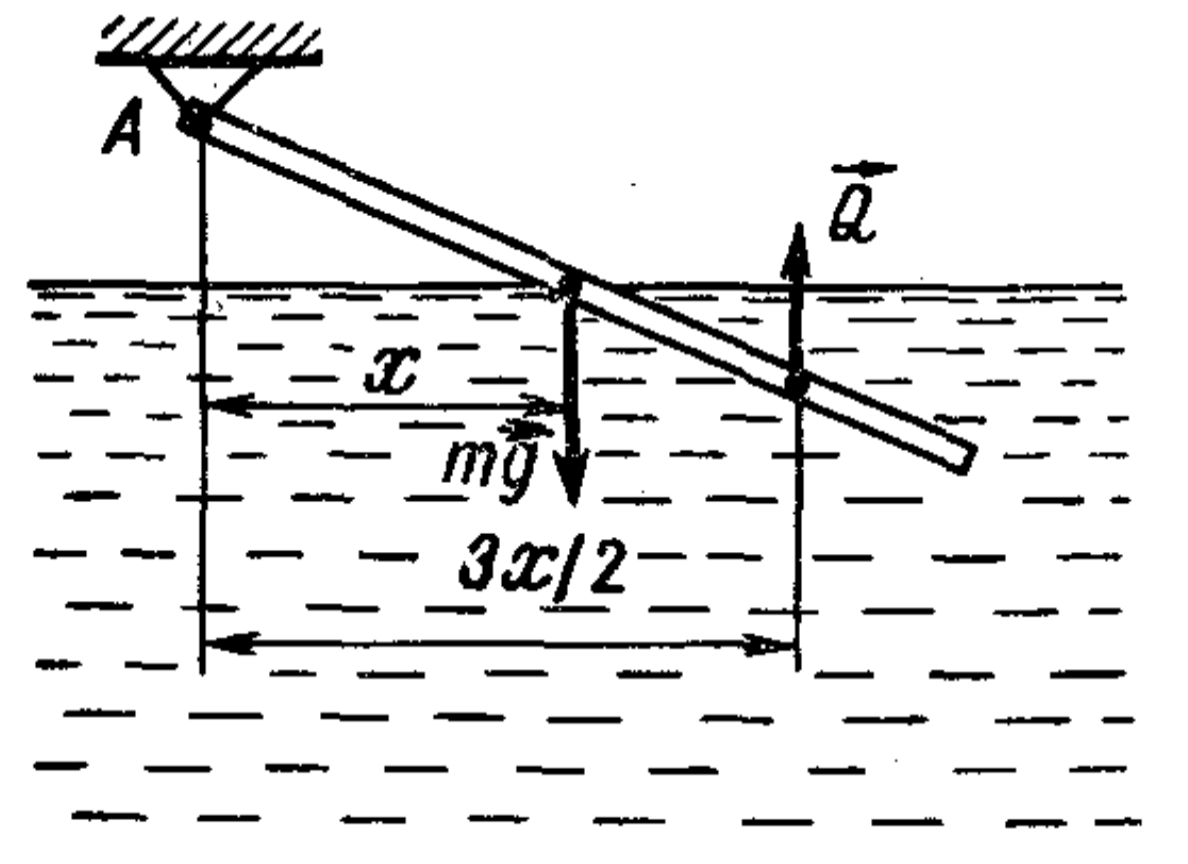
32. Two balls with radii \( r_1 \) and \( r_2 \), made of materials with densities \( \rho_1 \) and \( \rho_2 \), are connected by a weightless rod of length \( l \). The system is placed in a liquid with density \( \rho \) (\( \rho < \rho_1 \) and \( \rho < \rho_2 \)). At what point on the rod should it be suspended for the system to remain in equilibrium with the rod horizontal?
Answer
At a distance $x = l \frac{\rho_2 - \rho}{(\rho_2 - \rho) + (\rho_1 - \rho)(r_1/r_2)^3}$ from the sphere with density $\rho_1$.
Hint
The differences between the forces of gravity and Archimedean forces acting on the weights are respectively: $F_1 = \frac{4}{3} \pi r_1^3 (\rho_1 - \rho)g$ and $F_2 = \frac{4}{3} \pi r_2^3 (\rho_2 - \rho)g$. Since the rod with the weights is in equilibrium, $F_1 x = F_2 (l - x)$ ($x$ is the distance from the weight with density $\rho_1$ to the suspension point of the rod).
33. A tube with radius \( r \) and height \( h \) emerges from a vessel filled with water (see figure). The tube is closed by a circular plate of radius \( R \) and mass \( M \), pressed against the tube by water pressure. With what force \( F \) must the plate be pushed at point \( A \) to make it pivot and open the tube? The vessel is filled with water to height \( H \). The plate's thickness is negligible. 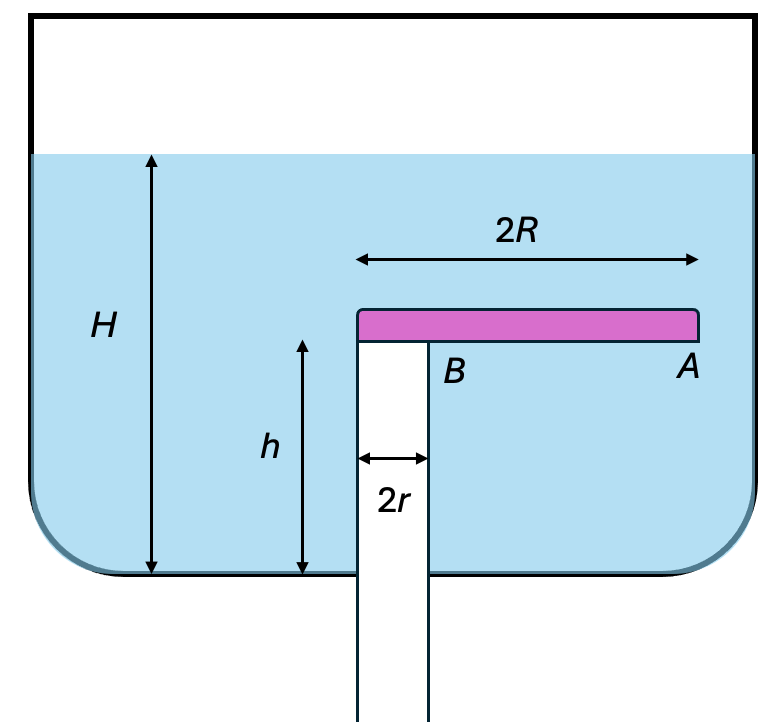
Answer
$F > \dfrac{\rho(H-h)\pi r^3 - M(R-2r)}{2(R-r)} g$.
Solution
The plate will rotate around point B (see the following figure). The water pressures from both sides of the plate balance each other everywhere except for the area above the tube. Here the water pressure force is $F = \rho g (H-h) \pi r^2$. Its moment relative to point B is $\rho g (H-h) \pi r^3$. The plate will turn over if $\rho g (H-h) \pi r^3 < Mg(R-2r) + F(2R-2r);$ $F > \frac{\rho(H-h)\pi r^3 - M(R-2r)}{2(R-r)} g.$ 
34. A body submerged in a liquid is balanced on a scale. Will the scale's reading change if the liquid and the submerged body are heated?
Answer
The answer depends on the ratio of the thermal expansion coefficients of the body and the liquid. If the thermal coefficient of the body is less than that of the liquid (as is usually the case), the body will outweigh.
35. A solid homogeneous body with volume \( V \) and material density \( \rho \) floats at the boundary between a heavy liquid (density \( \rho_1 \)) and a lighter liquid (density \( \rho_2 \)). What fraction of the body's volume \( V_1 \) will be submerged in the heavy liquid?
Answer
$V_1/V = (\rho - \rho_2)/(\rho_1 - \rho_2)$.
Solution
The mass of the body must be equal to the mass of the displaced liquids: $\rho V = \rho_1 V_1 + \rho_2 V_2$, where $V_1 + V_2 = V$. Solving these equations together, we find $V_1 = V \frac{\rho - \rho_2}{\rho_1 - \rho_2}$.
36. A wooden cube with side length 10 cm floats between oil and water, with 2.5 cm of its height below the oil's surface. The cube's bottom surface is 2.5 cm below the interface. What is the cube's mass \( m \), given the oil's density is \( 0.8 \, \text{g/cm}^3 \)? Determine the pressure forces \( F_1 \) and \( F_2 \) on the cube's top and bottom faces. Will the cube's submersion depth in water change if more oil is added?
Answer
$m \approx 0.85$ kg; $F_1 \approx 1.96$ N; $F_2 \approx 10.29$ N. Does not change.
Hint
See the solution to the previous problem.
37. A steel cube (density \( 7.8 \, \text{g/cm}^3 \)) floats in mercury (density \( 13.6 \, \text{g/cm}^3 \)). Water is poured over the mercury until it covers the cube with a thin layer. What is the height \( H \) of the water layer? The cube's edge length is \( a = 10 \, \text{cm} \). Determine the pressure \( p \) on the cube's bottom face.
Answer
$H \approx 4.6$ cm; $p \approx 7650$ Pa.
38. A piece of cork weighs \( 0.147 \, \text{N} \) in air, and a piece of lead weighs \( 1.1074 \, \text{N} \). If these pieces are tied together, suspended from a scale, and submerged in kerosene, the scale reads \( 0.588 \, \text{N} \). Determine the density of the cork, given the density of kerosene is \( 0.8 \, \text{g/cm}^3 \) and that of lead is \( 11.3 \, \text{g/cm}^3 \).
Answer
0.2 g/cm$^3$.
Solution
Let: mass of the cork $m_1$, its density $\rho_1$, mass of lead $m_2$, its density $\rho_2$. Then the volume of the cork $V_1 = m_1/\rho_1$, volume of lead $V_2 = m_2/\rho_2$, total volume $V = V_1 + V_2 = m_1/\rho_1 + m_2/\rho_2$. According to Archimedes' law, the buoyant force $F$ acts on the body immersed in the liquid [in our case $F = (m_1 + m_2)g - Q$, where $Q$ is the reading of the scales], equal to the weight of the displaced liquid in the volume of the immersed body $F = V \rho_3 g$, where $\rho_3$ is the density of kerosene. Hence $(m_1 + m_2)g - Q = (m_1/\rho_1 + m_2/\rho_2) \rho_3 g$. Solving the obtained equation for the unknown quantity $\rho_1$, we get $\rho_1 = \frac{m_1 g \rho_2 \rho_3}{[(m_1 + m_2)g - Q]\rho_2 - m_2 g \rho_3}$.
39. An open cylindrical glass is submerged into water in two ways: once with the base up and once with the base down, both to the same depth. In which case is the work required to submerge the glass greater? No water spills from the vessel, and no water enters the glass when submerged base-down.
Answer
When the beaker is immersed in the inverted position, water, compressing the air inside it, partially fills its internal volume. With the same immersion of the beaker in water, in the first case, the displaced volume of water is less than in the second case, and therefore the work is less.
40. Two balloon envelopes of equal mass—one made of elastic rubber, the other of rubberized fabric—are filled with the same amount of hydrogen and occupy equal volumes near Earth. Which balloon will rise higher, assuming no hydrogen escapes?
Answer
The thin rubber balloon will rise to a great height. At the same height above the Earth, the volume of the thin rubber balloon, and hence the buoyant force acting on it, will be greater than for the fabric balloon.
41. By what factor will the lifting force of the gas filling an aerostat (airship) change if helium is used instead of hydrogen?
Answer
Decreases by a factor of 1.08.
Solution
The lift force $F_L$ of a certain volume of gas is equal to the difference between the weight $m_{air}g$ of the air displaced by the gas and the weight $m_g g$ of the gas itself: $F_L = (m_{air} - m_g)g$. The ratio of the lift forces $(m_{air} - m_{water}) / (m_{air} - m_{helium})$ is equal to the ratio of the differences in molar masses, since the pressure $p$, volume $V$, and temperature $T$ are the same ($pV = mRT/\mu$). Consequently, $F_1/F_2 = (\mu_{air} - \mu_{H2}) / (\mu_{air} - \mu_{He}) = (29 - 2) / (29 - 4) = 27/25 = 1.08$.
42. A thin-walled tube of a mercury barometer is suspended from a dynamometer. What does the dynamometer show? Will its reading change with atmospheric pressure variations?
Answer
The dynamometer shows the sum of the weight of the tube and the force of atmospheric pressure on the tube, equal to the weight of mercury in the tube.
43. Estimate the mass of the gaseous envelope surrounding the Earth.
Answer
$m = p \cdot 4\pi R^2 / g \approx 5 \times 10^{18}$ kg, where $p$ is atmospheric pressure; $R$ is the radius of the Earth.
44. An L-shaped tube, with its long arm open, is filled with hydrogen. In which direction will the rubber film covering the short arm bulge?
Answer
The pressures of air and water at level I-I (see figure) are respectively equal: $p_1 = p_0 - \rho_{air} g h$, $p_2 = p_0 - \rho_{water} g h$, where $p_0$ is the pressure at level 0-0; $\rho_{air}$ and $\rho_{water}$ are the densities of air and water. Since $\rho_{water} > \rho_{air}$, then $p_1 > p_2$, and the film will be bent outwards. 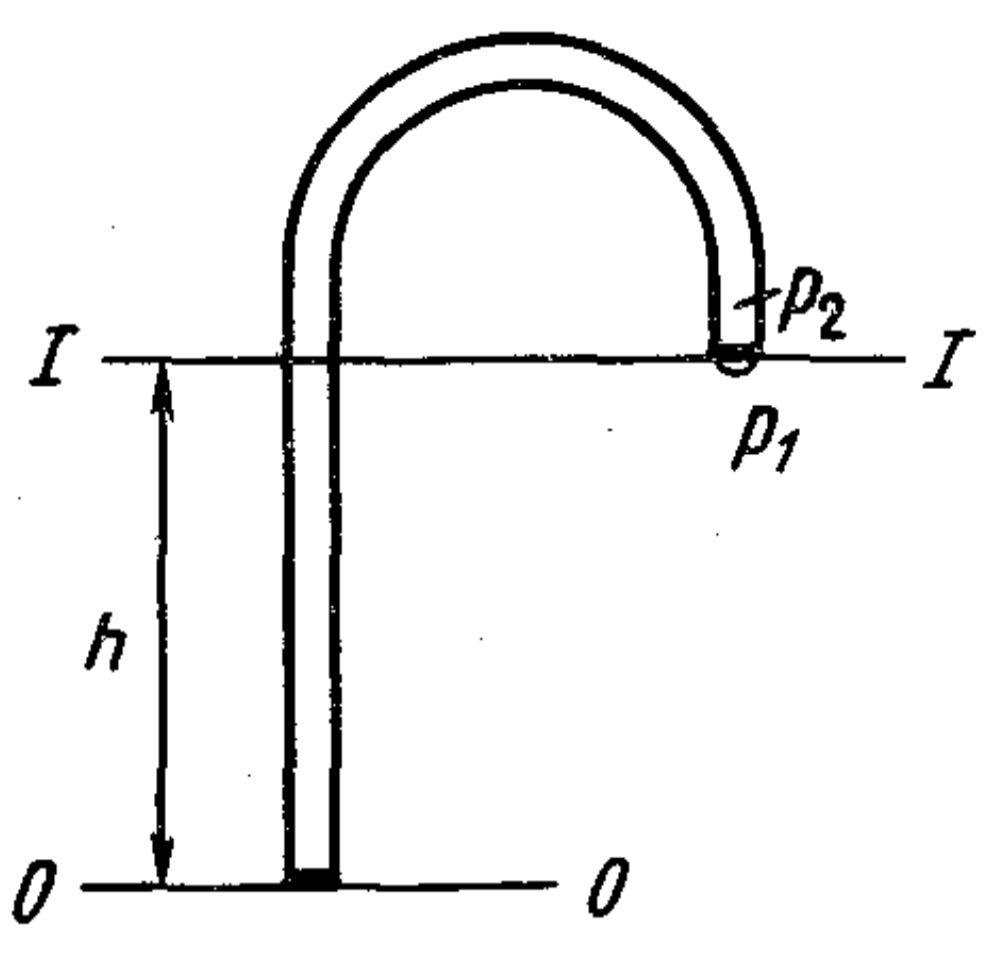
45. Water flows through a pipe with a constriction. An elastic rubber ball is released into the pipe. How will its diameter change as it passes through the narrow section?
Answer
It will increase, because the speed of water in the narrow part of the pipe is greater, and the pressure is correspondingly less than in the wide part of the pipe.
46. A body with mass \( m = 2 \, \text{kg} \) and volume \( V = 1000 \, \text{cm}^3 \) is located in a lake at depth \( h = 5 \, \text{m} \). What work must be done to lift it to a height \( H = 5 \, \text{m} \) above the water's surface? Is this work equal to the change in the body's potential energy? Explain the result.
Answer
$A = (m - \rho V)gh + mgH \approx 150$ J.
Solution
To move the body in water, a force $F = mg - F_{buoy} = mg - \rho V g$ ($\rho$ is the density of water) must be applied to it. Therefore, to lift the body from depth $h$ to height $H$ above the water surface, work must be done $A = (m - \rho V)gh + mgH \approx 150$ J. This work is less than the change in potential energy of the body $\Delta W_p = mg(h+H)$ by the amount $\rho V gh \approx 50$ J. The found difference is precisely the amount by which the potential energy of the water decreased when the body was lifted - volume $V$ of water descends from the surface to depth $h$.
47. A vertical tube with a piston is fixed in a reservoir such that its lower end is submerged in water. The piston, initially lying on the water's surface, is slowly raised to height \( H = 15 \, \text{m} \). What work is required to do this? The piston's area is \( S = 1 \, \text{dm}^2 \), and atmospheric pressure is \( p = 101 \, \text{kPa} \). Neglect the piston's weight.
Answer
$A = \frac{pS}{2} (2H - \frac{p}{\rho_0 g}) \approx 9800$ J, where $\rho_0$ is the density of water.
Solution
The water pressure directly under the pump piston is equal to $p - \rho_0 g h$ ($h$ is the piston lift height). The force lifting the piston is equal to the difference between the pressure forces above and below the piston, i.e., the value $F = [p_0 - (p_0 - \rho_0 g h)]S = \rho_0 g h S$. When the piston is lifted to a height $h = p_0 / (\rho_0 g) = 10$ m, this force increases linearly to the value $p_0 S$. Further, this force remains constant. Therefore, the work done in lifting the piston will be equal to: $A = \frac{p_0 S}{2} \frac{p_0}{\rho_0 g} + p_0 S (H - \frac{p_0}{\rho_0 g}) = \frac{p_0 S}{2} (2H - \frac{p_0}{\rho_0 g})$.
48. A submarine is at depth \( h = 100 \, \text{m} \). At what speed will water rush in through a hole in the submarine's hull? How much water will enter in one hour if the hole's diameter is \( d = 2 \, \text{cm} \)? The air pressure inside the submarine equals atmospheric pressure. Ignore changes in internal pressure.
Answer
$v \approx 44.3$ m/s; $V = 50$ m$^3$.
Solution
Applying Torricelli's formula for the outflow velocity from the opening $v^2 = 2gh$, we find $v = \sqrt{2gh}$. In time $t$, a volume of water $V = \pi d^2 v t / 4$ will enter the boat.
49. A water jet shoots from a hose. The flow rate is \( Q = 60 \, \text{L/min} \). What is the cross-sectional area \( S_1 \) of the jet at height \( h = 2 \, \text{m} \) above the hose's end if near the end it is \( S_0 = 1.5 \, \text{cm}^2 \)?
Answer
$S_1 \approx 4.37$ cm$^2$.
Solution
The speed of water at the end of the fire hose is $v_0 = Q/S_0$. Flying out of the fire hose, the water moves with uniform deceleration with acceleration $g$, therefore at height $h$ the speed of water $v_h = \sqrt{v_0^2 - 2gh}$. From the continuity equation of the stream $v_0 S_0 = v_h S_h$, which expresses that the mass of liquid flowing through any cross-section of the stream per unit time is the same, we get $S_h = \frac{v_0 S_0}{v_h} = \frac{Q}{\sqrt{(Q/S_0)^2 - 2gh}}$.
50. Why does a fast-moving bullet only make two small holes in an empty plastic cup, while a water-filled cup shatters into pieces when hit by a bullet?
Answer
During the time the bullet is in the glass, the water level in it does not have time to change. The resulting high-pressure region upon compression of the water spreads in all directions with the speed of sound, reaches the walls of the glass, and it shatters. This experiment illustrates the low compressibility of liquids.