Momentum. Law of Conservation of Momentum
1. A ball of mass $m = 100$ g, moving at a speed of $v = 1$ m/s, elastically collides with a plane. Determine the change in the ball's momentum if the angle between the velocity and the plane is $\alpha$, equal to: a) $90°$; b) $30°$.
Answer
a) $\Delta p = 2mv = 0.2 \text{ N} \cdot \text{s}$ (see figure, a in Solution);
b) $|\Delta p| = 2mv \sin \alpha = 0.1 \text{ N} \cdot \text{s}$.
Solution
b) The impulse of the ball can be resolved into two components: perpendicular to the plane and parallel to it (see figure, b). The latter does not change during the impact of the ball (since no forces act on the ball in this direction), while the normal component changes its direction to the opposite, maintaining its numerical value. Therefore, the ball reflects from the plane at the same angle at which it falls onto it. The change in the ball's impulse, as seen from the figure, is $2mv \sin \alpha$. 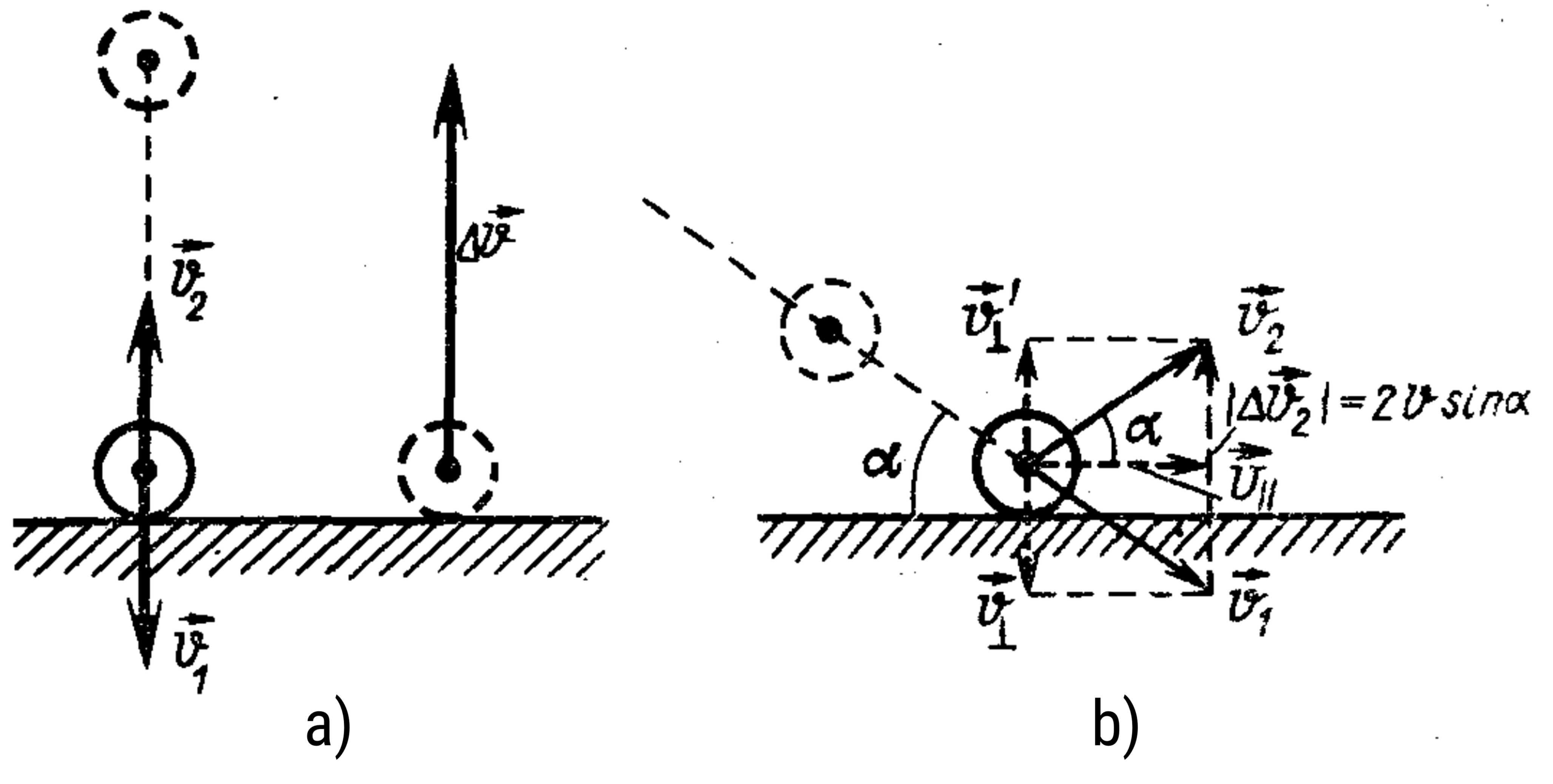
2. A ball of mass $m = 10$ g falls onto a horizontal plane from a height of $h_1 = 27$ cm. Find the average impact force $F_{cp}$ in the following cases:
a) the ball is made of clay (perfectly inelastic collision);
b) the ball and the plane are made of steel (perfectly elastic collision);
c) the ball is made of plastic and rises to a height of $h_2 = 12$ cm after the impact.
Consider the first two cases of the ball hitting a plane inclined at an angle of $\alpha = 30°$. Assume in all cases that the contact between the ball and the plane lasts (the duration of the impact) 0.03 s.
Answer
a) $F_{avg} = F'_{avg} = m\sqrt{2gh_1}/\Delta t + mg \approx 0.87$ H;
b) $F_{avg} = (2m\sqrt{2gh_1}/\Delta t + mg) \cos \alpha \approx 1.43$ H;
c) $F_{avg} = m\sqrt{2g}(\sqrt{h_1} + \sqrt{h_2})/\Delta t + mg \approx 1.38$ H.
Hint
Use Newton's second law in the form $\Delta(m\vec{v}) = \vec{f} \Delta t,$ where $\vec{f} = \vec{f}_p + m\vec{g}.$ Remember that impulse is a vector quantity, so in the third case $|\Delta(m\vec{v})| = mv_1 + mv_2.$ The change in the ball's impulse is directed upwards. According to Newton's third law, a force equal to $-\Delta(m\vec{v})/t$ and directed downwards will act on the plane during the impact.
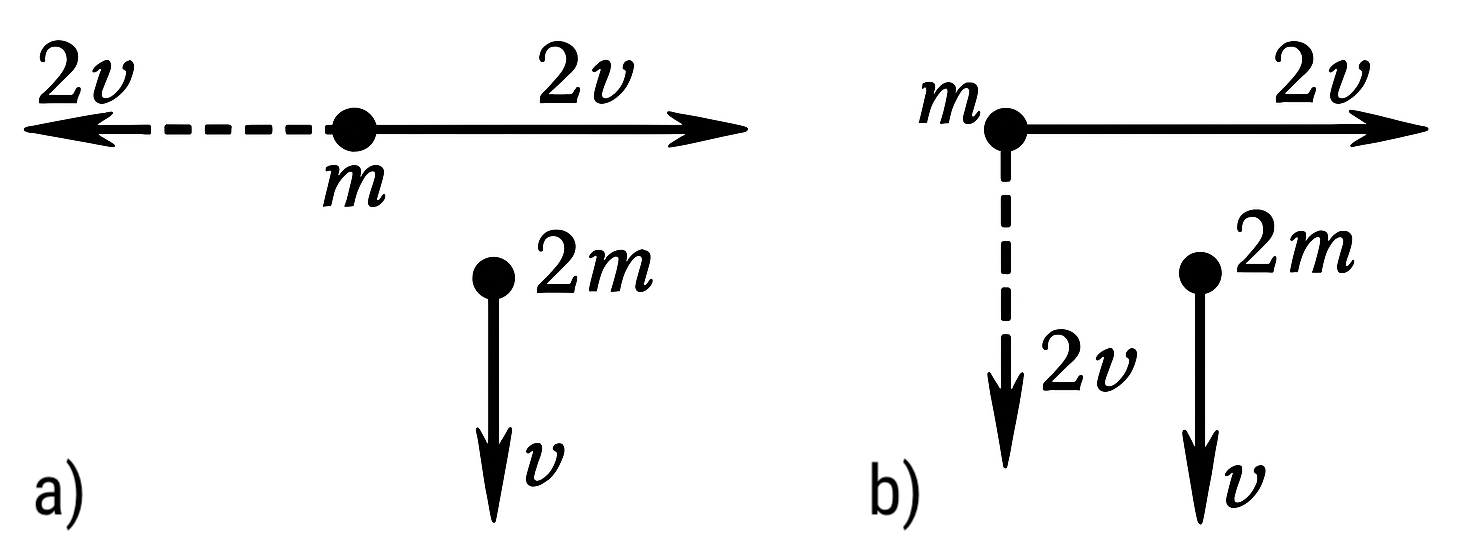
3. Two particles with masses $m$ and $2m$ move in mutually perpendicular directions with velocities $2v$ and $v$. The same force begins to act on the particles. Determine the magnitude and direction of the velocity of the particle with mass $2m$ at the moment when the velocity of the particle with mass $m$ becomes as shown by the dashed line:
a) in figure, a;
b) in figure, b.
Answer
a) $v\sqrt{5}$ at an angle $\alpha = \arctan 2$ to the initial direction;
b) $v\sqrt{5}$ at an angle $\beta = \arcsin(1/\sqrt{5})$ to the initial direction.
Solution
The change in the impulses of the particles is the same: the same forces acted on them for the same amount of time. In case a), the magnitude of the impulse change of the first particle is $2mv - (-2mv) = 4mv.$ The vector $\Delta \vec{p}$ is directed horizontally (figure, a). Therefore, the impulse of the second particle will be $\sqrt{(4mv)^2 + (2mv)^2} = mv\sqrt{20},$ and the speed is $v\sqrt{5}$, angle $\alpha = \arctan(4mv/2mv) = \arctan 2.$ Similarly, we find that in case b) the magnitude of the impulse change of the first particle is $2mv\sqrt{2}$ (figure, b). The impulse of the second particle changes similarly. Its magnitude will become $mv\sqrt{20}$ (this can be easily found using the cosine theorem). Its speed will accordingly be $v\sqrt{5}$; angle $\beta = \arcsin(1/\sqrt{5})$ (using the sine theorem). 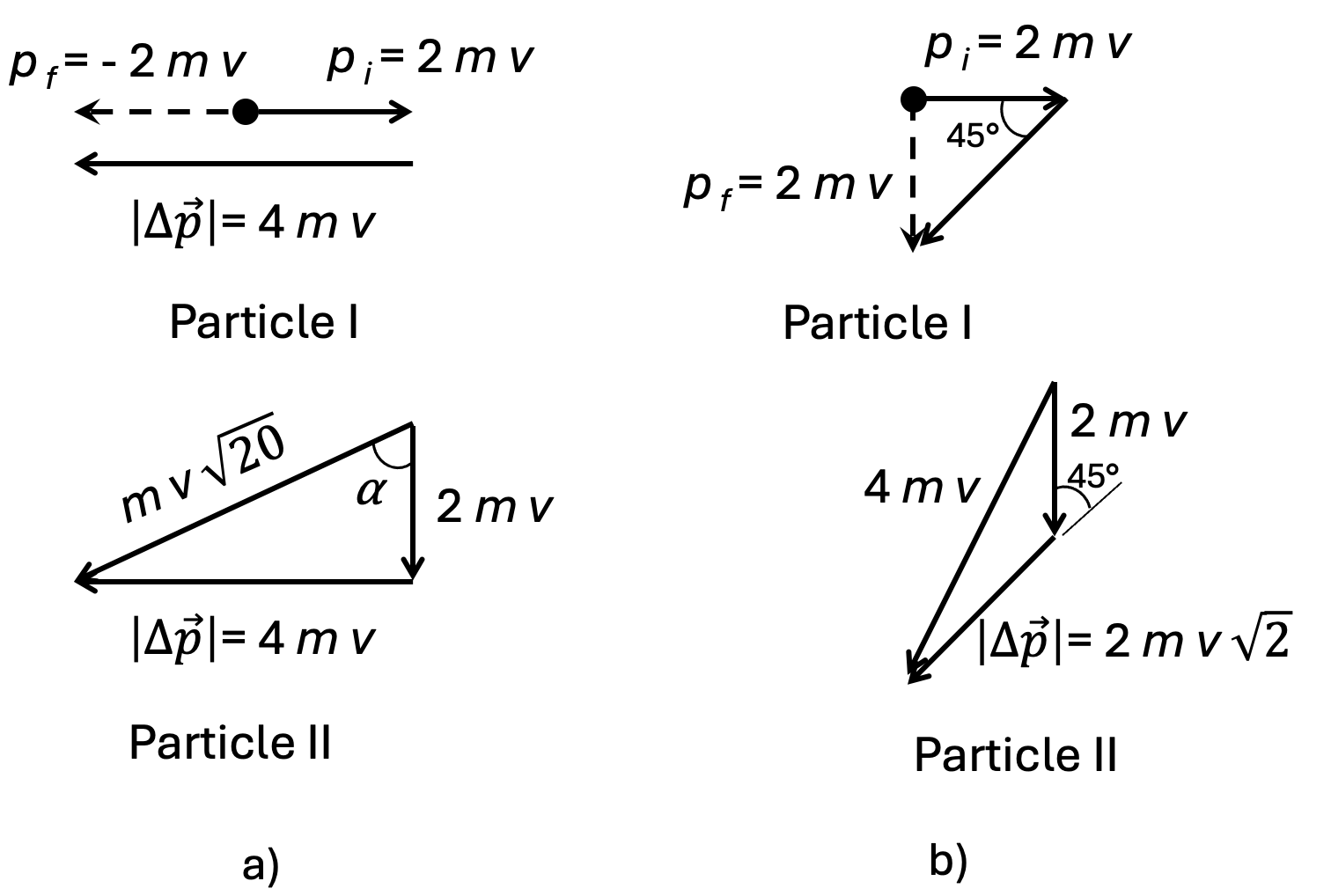
4. A water jet with a cross-sectional area of $S = 6$ cm² strikes a wall at an angle of $\alpha = 60°$ to the normal and bounces off elastically (without loss of speed). Find the force $F$ acting on the wall, if it is known that the water flow speed in the jet is $v = 12$ m/s.
Answer
$F = 2\rho Sv^2 \cos \alpha = 86.4$ N.
Hint
Note that in time $t$, the mass of water hitting the wall is the mass contained in a cylinder of length $l=vt$ and cross-section $S$, i.e., $m = \rho Svt$ ($\rho$ is the density of water).
5. A railway platform with a gun mounted on it moves at a speed of $v_1 = 9$ km/h. The total mass is $M = 20$ t. A projectile of mass $m = 25$ kg is fired from the gun at a speed of $v_2 = 700$ m/s relative to the center of mass. Determine the speed of the platform after the shot: a) when the shot is fired in the direction of the platform's movement; b) when the shot is fired in the opposite direction. Neglect the friction of the platform against the rails.
Answer
a) $u = v_1 - \dfrac{m}{M-m} v_2 \approx 1.62$ m/s;
b) $u = v_1 + \dfrac{m}{M-m} v_2 \approx 3.39$ m/s.
Hint
Since the change in the impulses of the platform and the projectile occurred due to the action of internal forces, the total change in their impulses should be zero.
6. A grenade flying at a speed of 10 m/s explodes into two fragments. The larger fragment, whose mass was 60% of the total mass of the grenade, continued to move in the same direction, but with an increased speed of 25 m/s. Find the speed of the smaller fragment.
Answer
12.5 m/s and will move in the direction opposite to the initial one.
7. A projectile at the highest point of its trajectory at a height of $h = 100$ m explodes into two parts: $m_1 = 1$ kg and $m_2 = 1.5$ kg. The projectile's speed at this point is $v_0 = 100$ m/s. The speed of the larger fragment $v_2$ turned out to be horizontal, coinciding in direction with $v_0$ and equal to 250 m/s. Determine the distance $s$ between the points where both fragments fall. Do not consider air resistance.
Answer
$s \approx 1695$ m.
Hint
From the law of conservation of momentum $(m_1 + m_2)v_0 = m_1 v_1 + m_2 v_2$, find $v_1 = \frac{(m_1 + m_2)v_0 - m_2 v_2}{m_1} = -125$ m/s. Consequently, $s = (v_1 + v_2)/2 \cdot \sqrt{2h/g} \approx 1695$ m.
8. A projectile fired from a gun at some angle to the horizon, at the highest point of its parabolic trajectory, explodes into two fragments of equal mass. One fragment returns to the gun along the previous trajectory after the explosion. Where will the second fragment fall? Will both fragments fall to the ground at the same time? Do not consider air resistance.
Answer
The second fragment will fall to Earth twice as far as the projectile would have fallen. They will fall simultaneously.
Hint
The fragment of the projectile that returned to the initial point obviously acquired a velocity equal in magnitude to the velocity of the projectile at the highest point of the trajectory, but opposite in direction, during the explosion. From the law of conservation of momentum, it follows that the second fragment after the explosion will have a velocity equal to three times the velocity of the projectile at the highest point.
9. A projectile explodes at the highest point of its trajectory at a height of $h = 19.6$ m into two identical parts. After a time $\tau = 1$ s after the explosion, one part falls to the Earth under the place where the explosion occurred. At what distance $s_2$ from the firing point will the second part of the projectile fall, if the first one fell at a distance of $s_1 = 1000$ m? Do not consider air resistance when solving the problem.
Answer
$s_2 = 5000$ m.
Solution
The law of conservation of momentum in this case is conveniently written for the projections of the impulses on the x and y axes (see figure) (since the time of rupture is short, the impulse of the gravity force can be neglected): $2mv_x = mv_{1x} + mv_{2x},\quad 2mv_y = mv_{1y} + mv_{2y},$ where $m$ is the mass of the fragment; $v_x, v_{1x}, v_{2x}, v_y, v_{1y}, v_{2y}$ are the projections of the velocities of the projectile and fragments on the x and y axes, respectively. Considering that the first fragment fell under the place of the projectile's rupture and therefore $v_{1x} = 0$, and also that the explosion occurred at the highest point of the trajectory and $v_y = 0$, we get: $v_{2x} = 2v_x,\quad v_{2y} = -v_{1y}.$ Since the projectile ruptured at the highest point of the trajectory $h = 19.6$ m, before the rupture it moved for $t = \sqrt{2h/g} = 2$ s, which means $v_x = s_1/t = 500$ m/s. Let's now write the equations for the coordinates of the first and second fragments: $x_1 = 0,\qquad y_1 = v_{1y}t - gt^2/2;$ $x_2 = v_{2x}t,\qquad y_2 = v_{2y}t - gt^2/2.$ Substituting $t=1$ s, $y_1 = y_2 = -h = -19.6$ m into the second and fourth equations and considering that $v_{2y} = -v_{1y}$, we find $t_2$ and then $x_2$. The distance from the firing point to the landing point of the second fragment $s_2 = s_1 + x_2$. 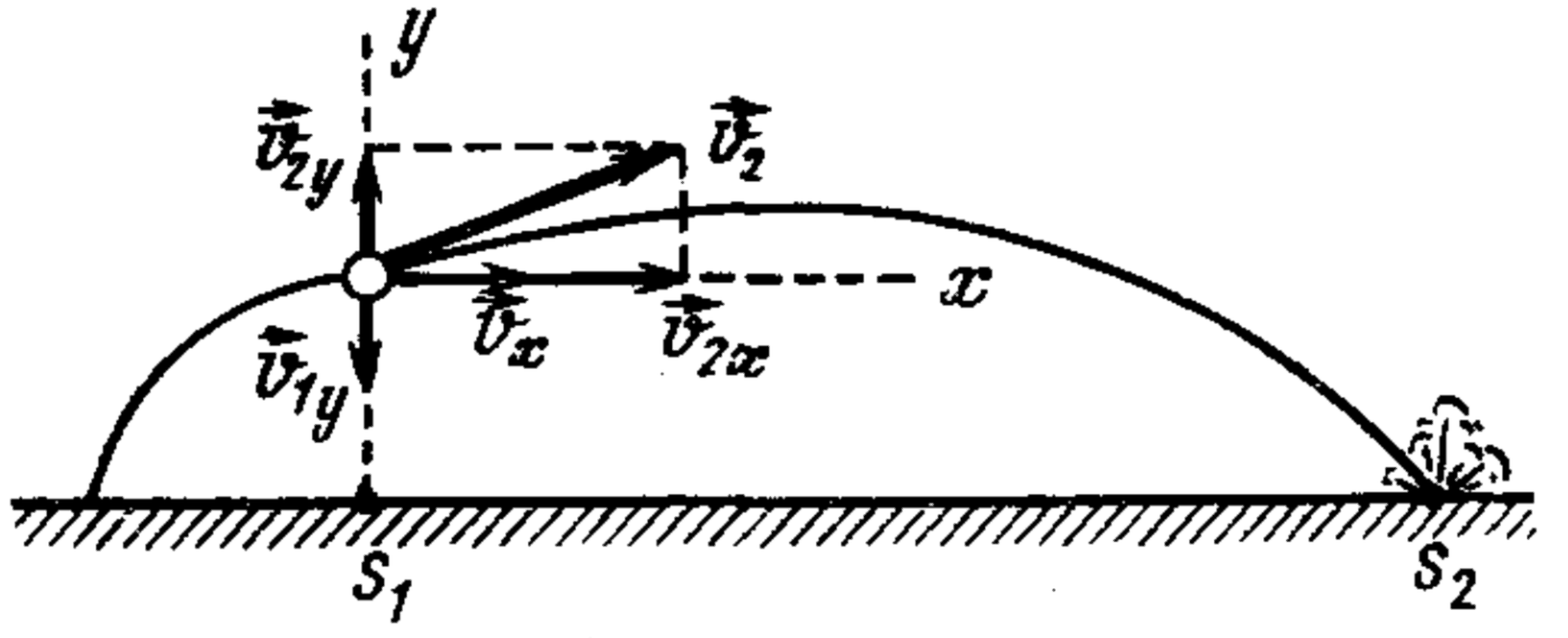
10. From a two-stage rocket with a total mass of $M = 1000$ kg at the moment of reaching a speed of $v_0 = 171$ m/s, its second stage with a mass of $m = 400$ kg separated, the speed of which increased to $v_2 = 185$ m/s. Find with what speed $v_1$ the first stage of the rocket began to move. The speeds are indicated relative to an observer on Earth.
Answer
$v_1 = \dfrac{Mv_0 - mv_2}{M-m} \approx 161.7$ m/s.
11. A spacecraft flies at a constant speed in a cloud of stationary micrometeoroid particles, which experience absolutely inelastic collisions with it. How many times do you need to increase the engine thrust so that:
a) the speed of the ship increases by a factor of two?
b) when entering a region of particles with a density three times greater, the speed of the ship does not change?
Answer
a) 4 times; b) 3 times.
Hint
The mass of particles entrained per unit time is $\dot{m} = m_0 n S v,$ where $m_0$ is the mass of one particle; $n$ is their number per unit volume (density); $S$ is the cross-sectional area of the spacecraft; $v$ is the speed of the spacecraft. Since the collisions are inelastic, the impulse imparted to the entrained mass per unit time is $m_0 n S v^2.$ According to Newton's third law, the force $F$ acting on the spacecraft is equal to the change in impulse of the mass interacting with it per unit time: $F = m_0 n S v^2;$ a) if $v$ increases 2 times, $F$ increases 4 times; b) if $n$ increases 3 times, $F$ increases by the same factor.
12. The third stage of the rocket consists of a carrier rocket with a mass of $m_p = 500$ kg and a head cone $m_k = 10$ kg. A compressed spring is placed between them. During tests on Earth, the spring imparted a speed of $v_{отн} = 5.1$ m/s to the cone relative to the carrier rocket freely suspended in a horizontal position. What will be the speeds of the cone $v_k$ and the rocket $v_p$ if their separation occurs in orbit when moving at a speed of $v = 8000$ m/s?
Answer
$v_k = 8005$ m/s; $v_p = 7999.9$ m/s.
Solution
Let's write the law of conservation of momentum in a reference frame moving with velocity $v$ in the direction of the rocket's flight. In this reference frame, before the cone separation, the rocket was at rest: $m_p \vec{v}_p' + m_k \vec{v}_k' = 0$ (here velocities $\vec{v}_p'$ and $\vec{v}_k'$ are algebraic quantities). According to the condition $v_k' = v_{rel} + v_p'$. Solving these equations together for $v_p'$, we find $v_p' = -m_k v_{rel} / (m_p + m_k)$. The velocity of the cone relative to the Earth is $v_k = v + v_k'$. The velocity of the rocket will be $v_p = v_k - v_{rel}$.
13. A homogeneous rod of length $l$ touches the smooth horizontal surface with its lower end. The upper end of the rod is suspended on a thread so that the rod forms an angle $\alpha$ with the horizontal plane. The thread is cut. In which direction and by how much will the lower end of the rod shift when it falls?
Answer
$\Delta x = l \sin^2(\alpha/2)$.
Hint
Since no forces act on the rod in the horizontal direction, its center of mass will move vertically.
14. Two balls with masses $m_1$ and $m_2$ are connected by a non-stretchable weightless horizontal rod. At the initial moment, the balls are given speeds $v_1$ and $v_2$ directed at angles $\alpha$ and $\beta$ to the horizon (see figure). What relationship should exist between the angles $\alpha$ and $\beta$ so that these speeds can be imparted to the balls? What is the nature of the system's movement? To what height will the center of mass of the system rise? 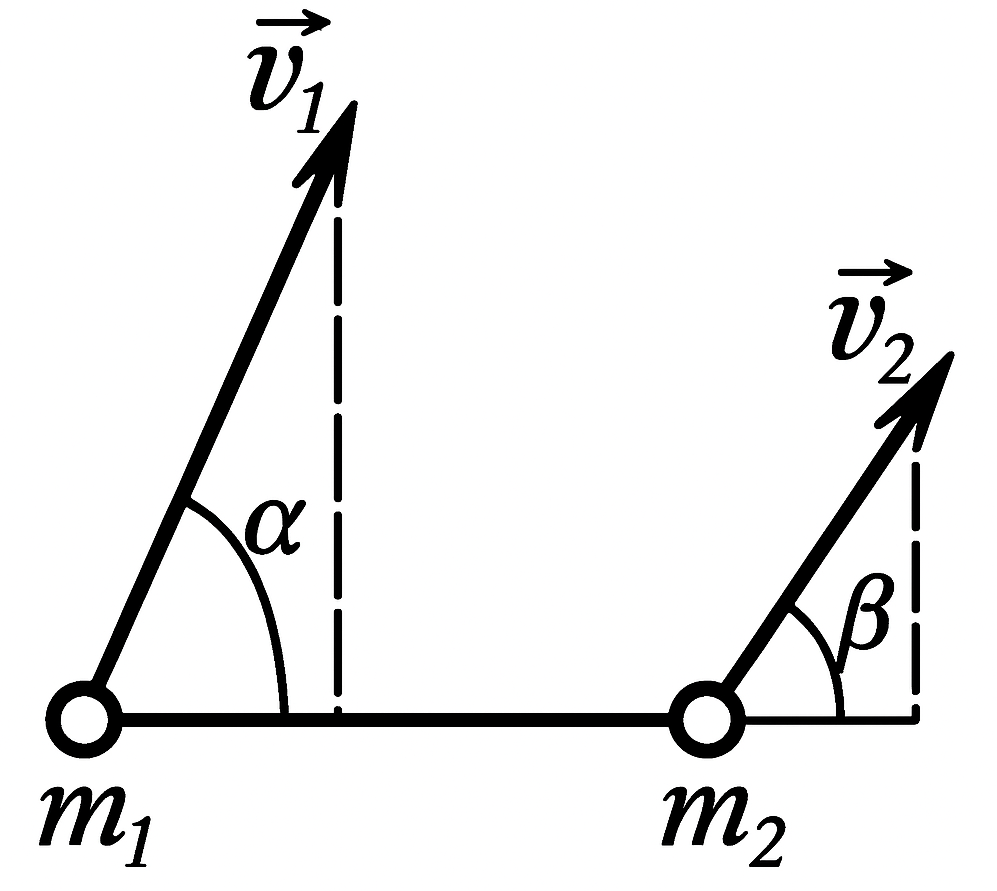
Answer
From the condition of inextensibility of the rod, it follows that $v_1 \cos \alpha = v_2 \cos \beta$, or $\cos \alpha / \cos \beta = v_2 / v_1$; the system will perform complex motion: rotate around the center of mass, which will simultaneously move along the trajectory along which a material point thrown at an angle to the horizon with an initial velocity $v_0 = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2}$ would move; the components of this velocity: horizontal $v_{0x} = v_1 \cos \alpha = v_2 \cos \beta,$ vertical $v_{0y} = \frac{m_1 v_1 \sin \alpha + m_2 v_2 \sin \beta}{m_1 + m_2};$ the height $h$ to which the center of mass of the system will rise is found from the law of conservation of energy $ \frac{1}{2}mv_{0y}^2 = mgh,$ whence $h = \frac{(m_1 v_1 \sin \alpha + m_2 v_2 \sin \beta)^2}{2g(m_1 + m_2)^2}.$
15. A person with a mass of $m = 70$ kg is on the stern of a boat located on a lake. The length of the boat is $l = 5$ m and its mass is $M = 280$ kg. The person moves to the bow of the boat. By what distance will the person move relative to the bottom?
Answer
The person will move a distance $x_1 = \frac{M}{M+m} l = 4$ m, and the boat a distance $x_2 = \frac{m}{M+m} l = 1$ m.
Solution
1st method. The impulse of an isolated system is constant, and its center remains at rest or maintains its velocity unchanged. Therefore, the position of the center of mass of the boat-person system $x_{cm}$ in the coordinate system associated (see figure) with the water should not change during the person's movement: $x_{cm} = \frac{Ma + ml}{M+m} = \frac{M(a+x_2) + mx_1}{M+m}$ ($x_2$ is the coordinate of the boat's nose after the person moves to the nose; $a$ is the coordinate of the boat's center of mass before the movement; $m$ is the mass of the person; $M$ is the mass of the boat). From this, we find that the boat moves a distance $x_2 = \frac{m}{M+m} l$ relative to the bottom, and the person a distance $x_1 = l - x_2 = \frac{M}{M+m} l$ relative to the bottom.
n2nd method. Denoting by $v$ the velocity of the person relative to the boat, and $u$ the velocity of the boat relative to the water, we can write: $m(v-u) = Mu$ [($v-u$) is the velocity of the person relative to the bottom], whence $u = \frac{m}{M+m} v.$ Considering that the paths traveled by the person and the boat are proportional to their velocities, we find the displacement of the boat relative to the bottom
$x_2 = \frac{m}{M+m} l,$ and the person $x_1 = \frac{M}{M+m} l.$
16. A boat is stationary on a lake. Fishermen are sitting on the stern and bow of the boat at a distance of $l = 5$ m from each other. The mass of the boat is $M = 150$ kg, the masses of the fishermen are $m_1 = 90$ kg and $m_2 = 60$ kg. The fishermen change places. How much will the boat move in this case? Neglect water resistance.
Answer
$x = (m_1 - m_2)l / (m_1 + m_2 + M) = 0.5$ m.
Hint
See the solution to problem 3.15, 1st method.
17. Three boats of the same mass $M$ are going in a line (one after the other) at the same speed $v$. From the middle boat, loads of mass $m$ are simultaneously thrown into the front and rear boats at a speed $u$ relative to the boat. What will be the speeds of the boats after the loads are thrown? Neglect water resistance.
Answer
$v_1 = \dfrac{m(v+u) + Mu}{M+m}$; $v_2 = u$; $v_3 = \dfrac{m(u-v) + Mu}{M+m}$.
Solution
Let's solve the problem in a reference frame moving with velocity $u$ relative to the shore. Obviously, in this reference frame, the boats before the cargo transfer are stationary. From the law of conservation of momentum, it follows: $mu = (M+m)v'_1,$ therefore the velocity of the front boat $v'_1 = mu/(m+M);\qquad 0 = (M+m)v'_2,$ for the middle boat $v'_2 = 0;\quad -mu = (M+m)v'_3,$ for the rear boat $v'_3 = -mu/(m+M).$ The velocity $v_1$ of the first boat relative to the Earth is obtained from the formula $v_1 = v'_1 + u,$ similarly we find the velocities of the 2nd and 3rd boats.
18. A trolley with a mass of $M = 120$ kg moves along rails without friction at a speed of $v = 6$ m/s. A person with a mass of $m = 80$ kg jumps off the trolley at an angle of $\alpha = 30°$ to the direction of its movement in the horizontal plane. The speed of the trolley decreases to $v' = 5$ m/s. What was the person's speed $u$ relative to the ground during the jump?
Answer
$u = \frac{(M+m)v - Mv'}{m \cos \alpha} \approx 8.6$ m/s.
Solution
The law of conservation of momentum can only be applied for the components of the impulses along the direction of motion, since external forces do not act on the system in this direction: $(M+m)v = Mv' + mu \cos \alpha.$ Hence $u = \frac{(M+m)v - Mv'}{m \cos \alpha}.$
19. Two pipes with cross-sections $S_1$ and $S_2$ are connected to each other, filled with explosive gas, and closed with pistons of masses $m$ and $M$ (see figure). After the explosion, the pistons fly out of the pipes. The first one flew out at a speed of $v_1$. At what speed $v_2$ did the second one fly out, if: a) the pipes are fixed; b) the mass of the pipes is $M_0$ and they are not fixed? What speed will the pipes have in this case? Neglect the friction of the pistons against the pipe walls and the mass of the gas. The time of movement of both pistons inside the pipes is the same. 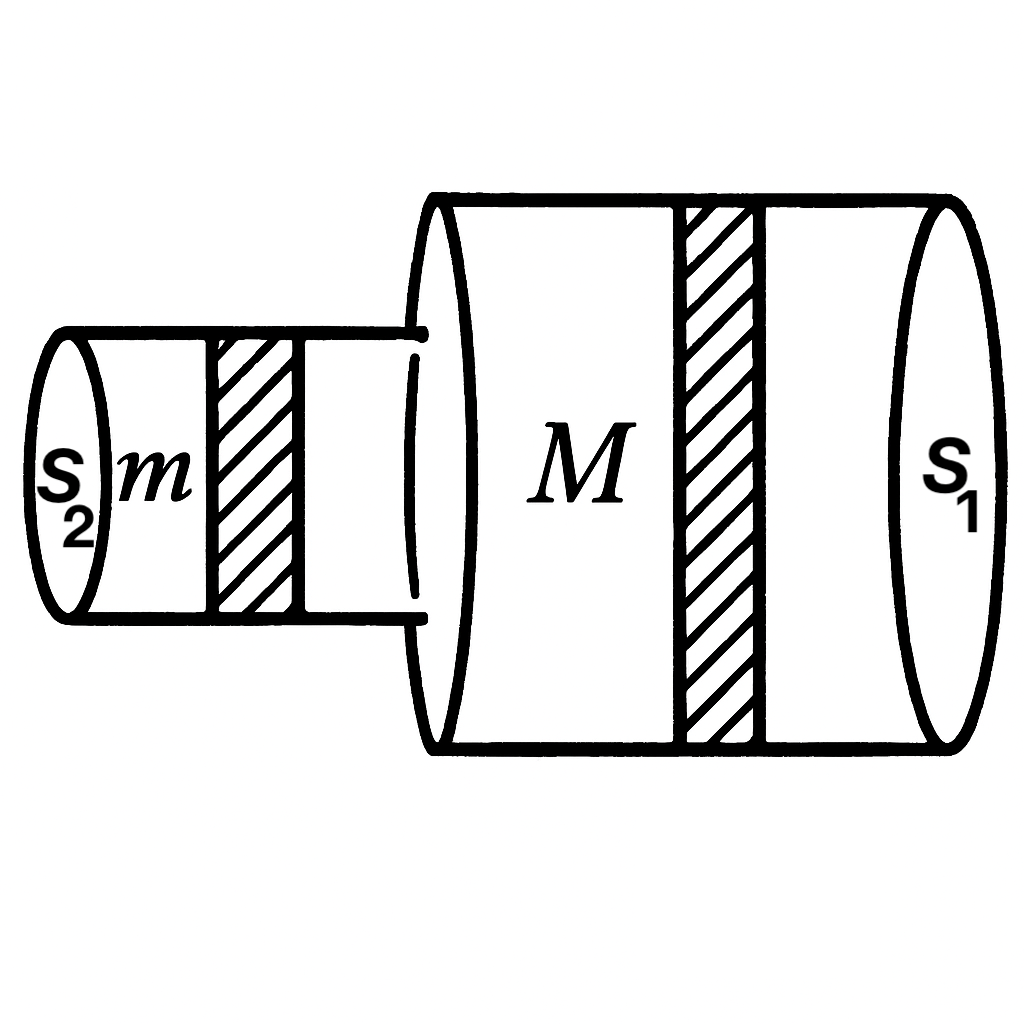
Answer
$v_2 = \frac{S_2}{S_1} \frac{m}{M} v_1$; $u = \frac{mv_1}{MS_1} (S_2 - S_1)$.
Solution
Considering that the forces acting on the pistons (gas pressure is the same) are proportional to the magnitudes of their surfaces $S_1$ and $S_2$ and the action time is the same, we can, using Newton's second law in 'impulse' form, obtain $mv_1 / Mv_2 = S_1 / S_2.$ Hence $v_2 = \frac{S_2}{S_1} \frac{m}{M} v_1$ in both cases. The velocity of the tubes in the second case can be easily found from the law of conservation of momentum: $mv_1 + M_0 u = M v_2.$ For $u$ we get: $u = \frac{m}{M_0} (\frac{S_2}{S_1} - 1) v_1.$
20. A box with sand of mass $M$ begins to slide without friction down an inclined plane making an angle $\alpha$ with the horizon. At the moment when the box has traveled a distance $l$, a body of mass $m$ falls into it, the speed of which is directed at an angle $\beta$ to the horizon. The box stops at this point. With what speed $v$ was the body moving?
Answer
$v = \dfrac{M\sqrt{2gl \sin \alpha}}{m \cos(\alpha \pm \beta)}$.
Solution
By the time the box with sand travels path $l$, it will have a speed $u = \sqrt{2al}$, where $a = g \sin \alpha$. For the box to stop, the sum of the projections of the impulses of the box and the body along the inclined plane must be zero: $-mv \cos(\alpha \pm \beta) + Mu = 0,$ the sign before $\beta$ is chosen depending on the direction of the body's velocity relative to the horizon (the interaction time of the body and the box is assumed to be small). Substituting the expression for $u$ into this equation, we get the answer.
21. A small body slides down a smooth inclined plane making an angle of $\alpha = 45°$ with the horizon from a height $h$. How will the body move if, at the end of the inclined plane, it encounters:
a) a perfectly elastic horizontal plane;
b) a horizontal plane that is inelastic but smooth?
Answer
a) Will describe a parabola above the plane, the vertex of which will be at height $h/2$;
b) will slide uniformly along the plane with velocity $v = \sqrt{gh}$.
Hint
a) The horizontal component of the body's velocity $v_x = \sqrt{2gh} \cos \alpha$ remains unchanged, while the vertical component $v_y = \sqrt{2gh} \sin \alpha$ will change its direction to the opposite upon impact. The trajectory of the body will be segments of parabolas.
b) The vertical component of the body's velocity will become zero, and the body will move uniformly with velocity $v = v_x = \sqrt{2gh} \cos \alpha$.
22. A vessel with water moves along an inclined plane with an angle of inclination $\alpha$ so that the water level is parallel to this plane (see figure). Water flows out of an opening near the bottom of the vessel at a speed $v$. Determine the coefficient of friction $k$ between the vessel and the plane, if the mass of the vessel with water is $m$, and the area of the opening is $S$. Neglect the change in the mass of water associated with its outflow from the vessel. 
Answer
$k = \rho Sv^2 / (mg \cos \alpha)$.
Solution
For the container with water, Newton's second law has the form $ma = mg \sin \alpha + F_p - kmg \cos \alpha.\tag{1}$ The forces acting on the container are shown below. From the condition that the water level is parallel to the inclined plane, it follows that the container with liquid moves along the inclined plane with acceleration $a = g \sin \alpha$ (see problem 2.17). The reaction force (reactive force) $F_p$, arising due to the outflow of the jet from the container, according to Newton's second (in impulse form) and third laws, is numerically equal to the change in the impulse of the water flowing out of the container per unit time: $F_p = \frac{\Delta(mv)}{\Delta t} = \frac{\rho S \Delta l}{\Delta t}v = \rho S v^2.$ Substituting the values of $a$ and $F_p$ into equation (1), we get $k = \frac{\rho S v^2}{mg \cos \alpha}.$ 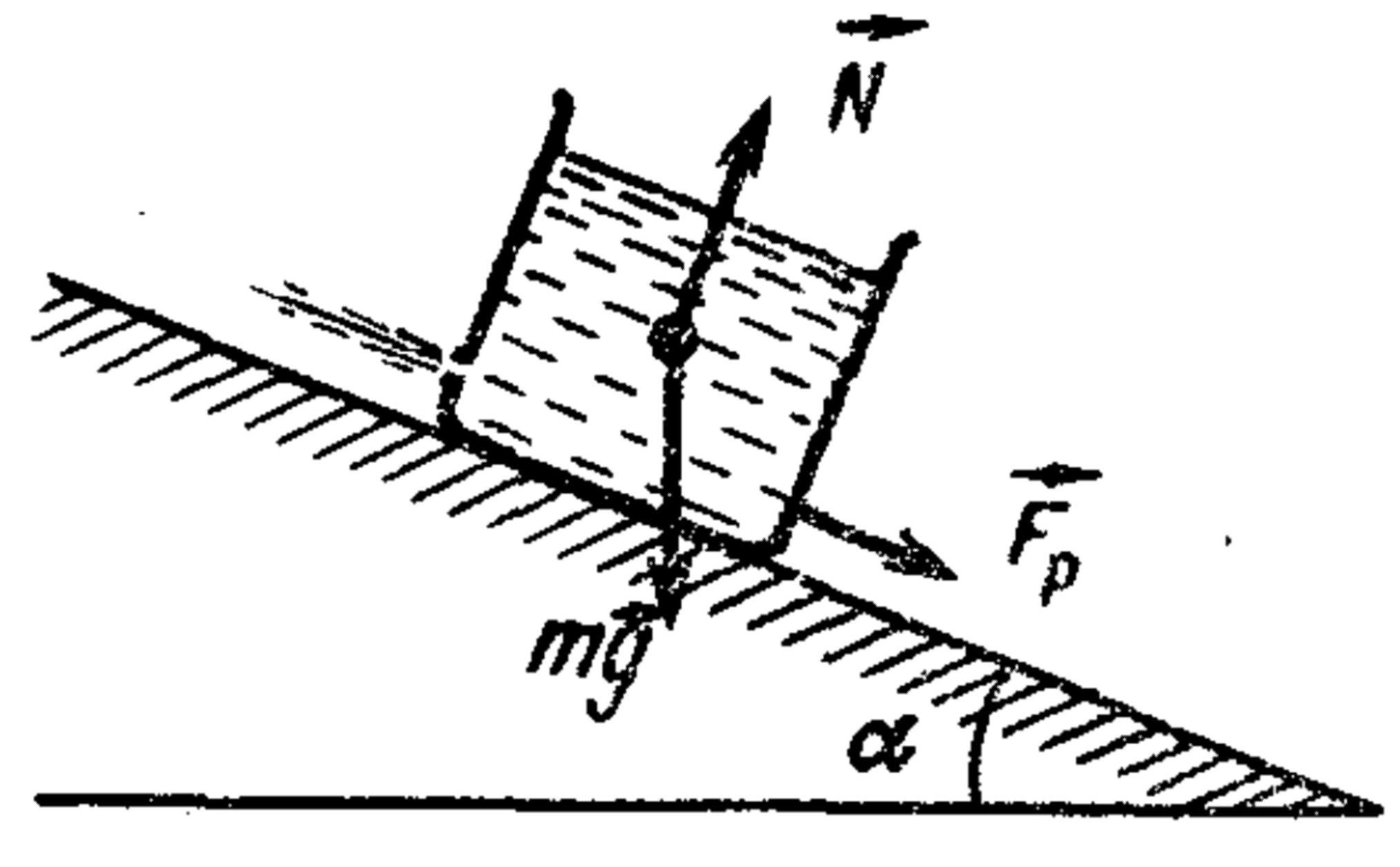
23. What external force causes a car to move?
Answer
The external force causing the car to move is the static friction force of the driving wheels on the road.
24. From a jet engine with a mass of $M = 0.5$ t, initially at rest, two portions of a substance are ejected sequentially in the horizontal direction at a speed of $v_0 = 1000$ m/s relative to the engine. The mass of each portion is $m = 25$ kg. What will be the speed of the engine $v_2$ after the second portion is ejected? There is no friction.
Answer
$v_2 = -mv_0 \left(\dfrac{1}{M} + \dfrac{1}{M-m}\right) \approx -102.6$ m/s.
Hint
The law of conservation of momentum when the first and second portions are ejected will be written respectively as: $(M-m)v_1 + m(v_0+v_1) = 0;\quad (M-2m)v_2' + m(v_0+v_2') = 0,$ where $v_1$ is the velocity acquired by the setup after ejecting the first portion. The second equation is written in a coordinate system moving with velocity $v_1$. (Here all velocities are algebraic quantities). From the recorded equations, find $v_1$ and $v_2'$ and finally $u_2 = v_1 + v_2'.$ (See also the solution to problem 25.)
25. Products of combustion are ejected from a rocket of mass $M$ in portions, the masses of which are $m$, at a speed $u$ relative to the rocket. Neglecting the effect of gravity and air resistance, determine the speed $u_n$ of the rocket after the release of the n-th portion.
Answer
$\displaystyle u_n = v \sum_{k=1}^{n} \frac{m}{M-(k-1)m} = v \left(\frac{m}{M} + \frac{m}{M-m} + ... + \frac{m}{M-(n-1)m}\right)$.
Solution
Let's write the law of conservation of momentum for the rocket-gas system when the k-th portion of gas is ejected in a reference frame moving with the velocity equal to the rocket's velocity after the ejection of the (k-1)-th portion: $(M-km)\Delta u_k = m(v - \Delta u_k)$, where $\Delta u_k$ is the velocity acquired by the rocket in this reference frame after the ejection of the k-th portion of gas; $(v - \Delta u_k)$ is the velocity of the k-th portion at the moment of its separation from the rocket, when their interaction ended and the latter had already acquired velocity $\Delta u_k$. Obviously, the velocity of the rocket relative to the Earth will be equal to the sum of the changes in its velocity $\Delta u_k$ associated with the ejections of gas portions from the first to the n-th: $u_n = \sum_{k=1}^{n} \Delta u_k = v (\frac{m}{M} + \frac{m}{M-m} + \frac{m}{M-2m} + ... + \frac{m}{M-(n-1)m}).$ This solution differs from the previous problem in that here all velocities are arithmetic quantities (vector magnitudes), and their assumed directions are taken into account when choosing signs, i.e., all velocity vectors are projected onto a single direction.
26. On a platform of mass $M$, which can move along a horizontal plane without friction, there are $n$ people, each of mass $m$. In which case will the platform be given a greater speed $u$: a) if each of them sequentially runs along the platform with a relative speed $u$ and jumps off onto the ground; b) in the case when all people simultaneously run along the platform and simultaneously jump off it with the same relative speed $u$? Analyze the case when these people are standing on the edge of the platform and jump off either one at a time or simultaneously.
Answer
In both cases a) and b) the answers are the same:
a) $u = v (\frac{m}{M+nm} + \frac{m}{M+(n-1)m} + ... + \frac{m}{M+m})$ (see solution to problem 25);
b) $u = v nm / (M+nm)$.
In cases a), as seen from the answers, the speed of the raft is greater.
27. A rocket of mass $M$ is launched vertically. The exhaust gas velocity from the engine nozzle is $u$. At what fuel consumption rate $μ$ (mass per unit time) will the engine thrust be sufficient to: a) balance the force of gravity acting on the rocket; b) give the rocket an acceleration of $a = 19.6$ m/s².
Answer
a) $\mu_1 = Mg/v$; b) $\mu_2 = M(a+g)/v$.
Solution
If the fuel consumption rate is $\mu$, and the velocity of gas ejection from the nozzle is $v$, then per unit time the rocket is imparted an impulse $\mu v$, which, according to Newton's laws, is equal to the reactive force. Therefore:
a) $\mu_1 v = Mg$, $\mu_1 = Mg/v$;
b) $Ma = \mu_2 v - Mg$, $\mu_2 = M(a+g)/v$.