Let us hang a weight on a spring balance. The spring will stretch and show how much the weight weighs. Without taking the weight off the spring balance, let us submerge it in water. Will the reading of the spring balance change? Yes, the weight of the body seems to decrease. If the experiment is done with an iron kilogram weight, the “loss” in weight will constitute approximately 140 grams.
But what is the matter? For it is clear that neither mass of the weight nor its attraction by the Earth could have changed. There can be only one cause of the loss in weight: an upward force of 140 gf acts on the weight submerged in water. But where does this buoyant force discovered by the great scientist of antiquity, Archimedes, come from? Before considering a solid body in water, let us consider “water in water”. We conceptually single out an arbitrary volume of water. This volume possesses weight, but does not fall to the bottom. Why? The answer is obvious—the hydrostatic pressure of the surrounding water prevents this. This implies that the resultant of this pressure in the volume under consideration is equal to the weight of the water and directed vertically upwards.
If this volume is now occupied by a solid body, it is clear that the hydrostatic pressure will remain the same.
Thus, as a result of hydrostatic pressure, a force acts on a body immersed in a fluid. The force is directed vertically upwards and is equal in magnitude to the weight of the fluid displaced by the body. This is Archimedes’ principle.
It is said that Archimedes lay in a bath-tub and thought about how to determine whether or not there is any silver in a gold crown. A person taking a bath distinctly feels a buoyant force. Suddenly the principle came to light, presented itself to Archimedes in its remarkable simplicity. With a cry of “Eureka!” (which means “I found it!”), Archimedes jumped out of the bath-tub and ran into the room containing the precious crown in order to immediately determine its loss of weight in water.
The loss of weight of a body in water will be equal to the weight of the water displaced by the body. Knowing the weight of the water, we shall immediately determine its volume, which is equal to the volume of the crown. Knowing the weight of the crown, we can immediately find the density of the material out of which it was made and, knowing the density of gold and silver, find the fraction of silver in the crowd.
Archimedes’ principle is valid, of course, for any fluid. If a body of volume \(V\) is immersed in a fluid of density \(\rho\), then the weight of the displaced fluid—and this is just the buoyant force—will be equal to \(\rho gV\).
The working of simple instruments controlling properties of fluid products is based on Archimedes’ principle. If alcohol or milk is diluted in water, its density will change; but it is possible to judge its composition on the basis of its density. Such a measurement is simply and easily performed with the aid of an areometer Figure 1.
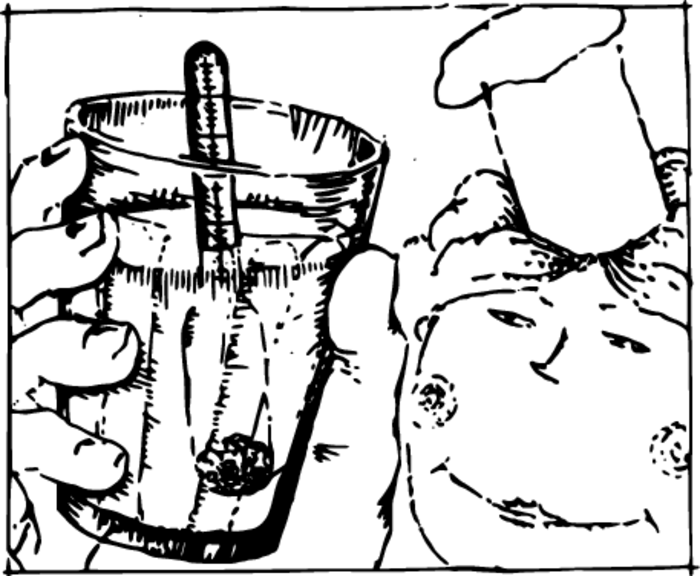
An areometer lowered into a liquid will be immersed to a greater or smaller depth depending on its density. An areometer will be in a state of equilibrium when the buoyant force becomes equal to the weight of the areometer.
Divisions are marked off on an areometer, and the density of a liquid is read from the marking which appears at its surface. Areometers applied for the control of alcohol are called alcoholometers, and those for the control of milk lactometers.
The average density of a person’s body is somewhat greater than unity. Anyone unable to swim will drown in fresh water. Salt water has a density greater than unity. The salinity of the water in most seas is insignificant, and its density, although greater than unity, is less than the average density of the human body. The density of the water in the Bay of Kara-Bogaz-Gol in the Caspian Sea is 1.18. This is greater than the average density of the human body. It is impossible to drown in this bay. One can lie on the water and read a book.
Ice floats on water. The preposition “on”, incidentally, is somewhat out of place here. The density of ice is about 10% less than that of water, so it follows from Archimedes’ principle that approximately nine-tenth of a piece of ice is submerged in water. It is precisely this circumstance that makes it so dangerous for ocean liners to come across icebergs.
If a balance scale is in equilibrium in air, this does not imply that it will be in equilibrium in a vacuum. Archimedes’ principle refers to air to the same degree as to water. A buoyant force equal to the weight of the displaced air acts on a body in air. A body “weighs” less in air than in a vacuum. The greater the volume of a body, the greater will be its loss of weight. A ton of wood loses more weight than a ton of lead. To the humorous question of which is lighter, there is the same kind of answer: a ton of lead is heavier than a ton of wood if they are weighed in air.
The loss of weight in air is slight as long as we are considering small bodies. However, in weighing a piece the size of a room, we would “lose” several tens of kilograms. For exact weighing, the correction due to the loss of weight of large bodies in air should be taken into account.
The buoyant force in air permits us to construct balloons, aerostats and dirigibles of various types. For this one must have a gas lighter than air.
If a balloon of volume 1 m\(^3\) is filled with hydrogen, 1 m\(^3\) of which has a weight equal to 0.09 kgf, then the lift—the difference between the buoyant force and the weight of the gas—will equal \[1.29~\mathrm{kgf} - 0.09~\mathrm{kgf} = 1.20~\mathrm{kgf}\] 1.29 kg/cm\(^3\) is the density of air.
Hence, a load of about a kilogram can be attached to such a balloon, and this will not prevent it from flying above the clouds.
It is clear that with relatively small volumes—of several hundred cubic metres—hydrogen balloons are capable of raising considerable loads into the air.
A serious defect of hydrogen aerostats is the inflammability of hydrogen. Together with air, hydrogen forms an explosive mixture. Tragic accidents have marked the history of the creation of aerostats.
Therefore, when helium was discovered, people started filling balloons with it. Helium is twice as heavy as hydrogen and the lift of a balloon filled with it is smaller. But will this difference be significant? The lift of a 1 m\(^3\) balloon filled with helium is found as the difference \(1.29~\mathrm{kgf} - 0.18~\mathrm{kgf} = 1.11~\mathrm{kgf}\). The lift has decreased by only 8%. At the same time, the advantages of helium are obvious.
The aerostat was the first apparatus with whose aid people rose in the air. Aerostats with a hermetically sealed car have been used up to the present day for investigating the upper layers of the atmosphere. They are called stratospheric balloons. They rise to a height of more than 20 km.
Balloons equipped with various measuring devices and transmitting the results of their measurements by radio Figure 2 are widely used at the present time. Such radiosondes contain miniature radio transmitters with batteries which report on the humidity, temperature and atmospheric pressure at various heights by means of prearranged signals.

One can send an unguided aerostat on a long journey and determine rather accurately where it will land. For this it is necessary that the aerostat climb to a great height, of the order of 20–30 km. Air currents are extremely stable at such heights, and the path of the aerostat can be calculated quite well beforehand. When necessary, one can automatically change the lift of the aerostat by letting out gas or throwing off ballast.
Aerostats on which a motor with a propeller was installed were previously used for flights. Such airships were streamlined. Airships lost the competition with airplanes even in comparison with planes of 30 years ago, they are clumsy, difficult to control, move slowly and have a “low ceiling”. It is believed that airships would be advantageous for carrying cargo.