If a ball lying in a depression is pushed, it will begin moving up the hill, gradually losing its kinetic energy. When it is completely lost, an instantaneous halt will occur and a downward motion will begin. Its potential energy will now be transformed into kinetic one. The ball will gain speed, rush past the equilibrium position by inertia and begin ascending again, only in the opposite direction. If the friction is insignificant, such an “upward-downward” motion can continue very long, while in the ideal case-in the absence of friction—it will continue indefinitely.

Therefore, motions near the position of stable equilibrium always have an oscillatory nature.

For studying oscillation, a pendulum is perhaps more suitable than a ball rolling back and forth in a hole, at least to the extent that it is easier to reduce the friction exerted on a pendulum to a minimum.

When a pendulum bob is deflected to its highest position, its speed and kinetic energy are equal to zero. Its potential energy is greatest at this moment. The bob goes down—the potential energy decreases and is transformed into kinetic one. Hence, the speed of the motion increases too. When the bob passes through its lowest position, its potential energy is least, and correspondingly the kinetic energy and speed are maximum. As the motion continues, the bob again rises. The speed now diminishes and the potential energy increases.

If we abstract from the friction losses, the bob will be deflected by the same distance to the right as it was originally deflected to the left. Its potential energy was transformed into kinetic one and then the same amount of “new” potential energy was created. We have described the first half of a single oscillation. The second half takes place in the same way, only the bob moves in the opposite direction.

Oscillatory motion is a repeating or, as one says, periodic motion. Returning to its starting point, the bob repeats its motion each time (if the changes resulting from friction are not taken into account) both with respect to its path and to its velocity and acceleration. The time spent on a single oscillation, i.e. in returning to the starting point, is identical for the first, second and all subsequent oscillations. This time—one of the most important characteristics of an oscillation is called the period; we shall denote it by \(T\). After this time, the motion is repeated, i.e, after the time \(T\), we shall always find a vibrating body at the same point in space and moving in the same direction. After a half-period, the displacement of the body and also the direction of the motion change sign. Since the period \(T\) is the time for one oscillation, the number \(n\) of oscillations in a unit of time will be equal to \(1/T\).

But what does the period of vibration of a body moving not far from the position of stable equilibrium depend on? In particular, what does the period of oscillation of a pendulum depend on? Galileo was the first to pose and solve this problem. We shall now derive Galileo’s formula.

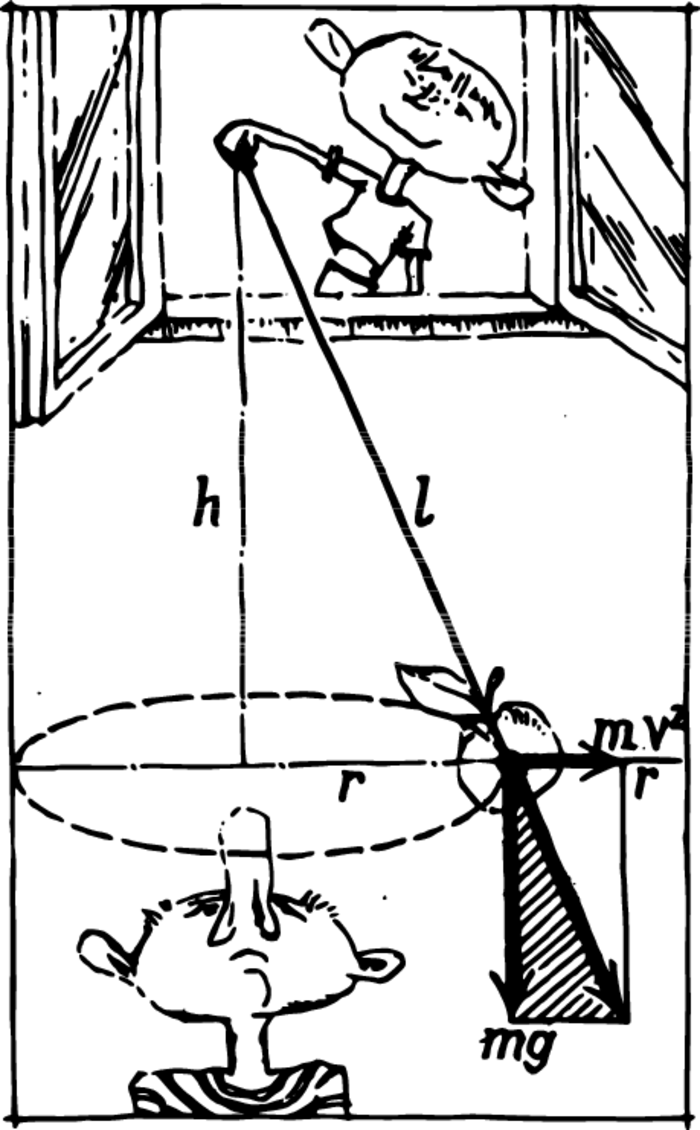
However, it is difficult to apply the laws of mechanics to non-uniformly accelerated motion in an elementary manner. Therefore, in order to bypass this difficulty, we shall not make the pendulum bob oscillate in a vertical plane, but have it describe a circle, remaining at a fixed height all the time. It isn’t difficult to create such a motion-one merely has to remove the pendulum from its equilibrium position and give it an initial push with a properly chosen force in the direction exactly perpendicular to the radius of deflection.

Such a “conical pendulum” is depicted in Figure 1.

The bob of mass \(m\) moves around a circle. Hence, besides the force of gravity \(mg\), a centrifugal force of \(mv^{2}/r\), which we may also represent in the form \(4 \pi^{2} n^{2} rm\) is exerted on it. Here \(n\) is the number of revolutions per second. We may therefore also write out our expression for the centrifugal force as follows: \(4 \pi^{2} rm/T^{2}\). The resultant of these two forces pulls on the cord of the pendulum.

Two similar triangles—the force triangle and the distance triangle—are shaded in the figure. The ratios of the corresponding legs are equal; hence \[\frac{mgT^{2}}{4 \pi^{2}rm} = \frac{h}{r}\,\ \textrm{or} \,\ T = 2 \pi \sqrt{\frac{h}{g}}\] What factors does the period of oscillation of a pendulum depend on? If we perform experiments at one and the same location on the Earth (\(g\) doesn’t change), the period of oscillation depends only on the difference in height between the point of suspension and the point where the bob is. The mass of the bob, as always in a gravitational field, does not affect the period of oscillation.

The following circumstance is of interest. We are investigating motion near the position of stable equilibrium. For small deflections, we may replace the difference in height \(h\) by the length \(l\) of the pendulum. It is easy to verify this. If the length of the pendulum is \(1\,\mathrm{m}\) and the radius of deflection is \(1\,\mathrm{cm}\), then \[h = \sqrt{10 000 - 1} = 99.995\,\mathrm{cm}\] The difference between \(h\) and \(l\) will reach 1% only when the deflection is \(14\,\mathrm{cm}\). Consequently, the period of the free oscillations of a pendulum for not too large a deflection from the equilibrium position is \[T = 2 \pi \sqrt{\frac{l}{g}}\] i.e. depends only on the length of the pendulum and the value of the acceleration of free fall at the place where the experiment is performed, but does not depend on the magnitude of the deflection of the pendulum from equilibrium position.

The formula \(T = 2\pi \sqrt{l/g}\) has been proved for a conical pendulum. What will it look like for a simple “plane” pendulum? It turns out that this formula retains its form. We shall not prove this rigorously, but call attention to the fact that the shadow cast onto a wall by the bob of a conical pendulum will oscillate almost like a plane pendulum: the shadow completes one oscillation during just the same time in which the bob describes a circle.

The use of small oscillations about an equilibrium position permits the measurement of time with very great accuracy.

According to legend, Galileo established the independence of the period of oscillation of a pendulum of its amplitude and mass while observing during services in a cathedral how two enormous chandeliers were swinging.

Therefore, the period of oscillation of a pendulum is proportional to the square root of its length. Thus, the period of oscillation of a metre-long pendulum is twice that of a \(25\,\mathrm{cm}\) pendulum. It also follows from our formula for the period of oscillation of a pendulum that one and the same pendulum will not oscillate equally fast at different latitudes on the Earth. As we move closer to the equator, the acceleration of free fall decreases and the period of oscillation grows.

It is possible to measure a period of oscillation with a very great degree of accuracy. Therefore, experiments with pendulums enable us to measure the acceleration of free fall very accurately.