What has been said so far refers to oscillations near an equilibrium position, taking place under the action of a restoring force whose magnitude is directly proportional to the displacement of a point from its equilibrium position. Such motions occur in accordance with a sinusoidal law. They are called harmonic. The period of harmonic oscillations is independent of the amplitude.

Oscillations with a large amplitude are much more complex. Such oscillations do not occur in accordance with a sinusoidal law, and their display yields more complicated curves different for various oscillating systems. The period is no longer a characteristic property of the oscillation and depends on the amplitude.

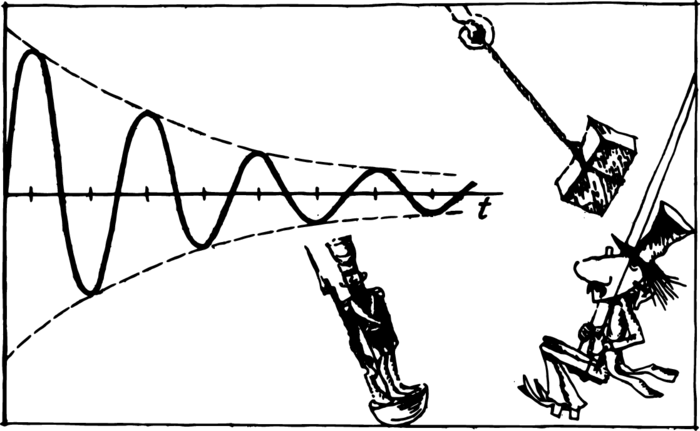
Friction will significantly change any oscillations. In the presence of friction, oscillations gradually damp. The greater the friction, the faster the damping occurs. Try making a pendulum immersed in water oscillate. It is unlikely that you will succeed in getting the pendulum to complete more than one or two oscillations. If a pendulum is immersed in a very viscous medium, there may fail to be any oscillation at all. The deflected pendulum will simply return to its equilibrium position. A typical graph for a damped oscillation is shown in Figure 1. The deviation from the equilibrium position has been plotted along the vertical axis, and the time along the horizontal one. The amplitude of a damped oscillation diminishes with each oscillation.