During every oscillation about an equilibrium position, there is a force acting on the vibrating body “desiring” to return it to the equilibrium position. When a point is receding from its equilibrium position, the force decelerates its motion; when it is approaching this position, the force accelerates its motion.

Let us examine this force in the case of a pendulum (Figure 1). The bob of the pendulum is acted upon by the force of gravity and tension in the string. Let us decompose the force of gravity into two components – one directed along the string and the other perpendicular to it, along the tangent to the path. Only the tangential component of the gravitational force is of significance for the motion. I t is precisely the restoring force in this case. As for the force directed along the string, it is balanced by the reaction on the part of the nail on which the pendulum is hanging, and it is only necessary to take it into account when we are interested in whether the string will withstand the weight of the vibrating body.

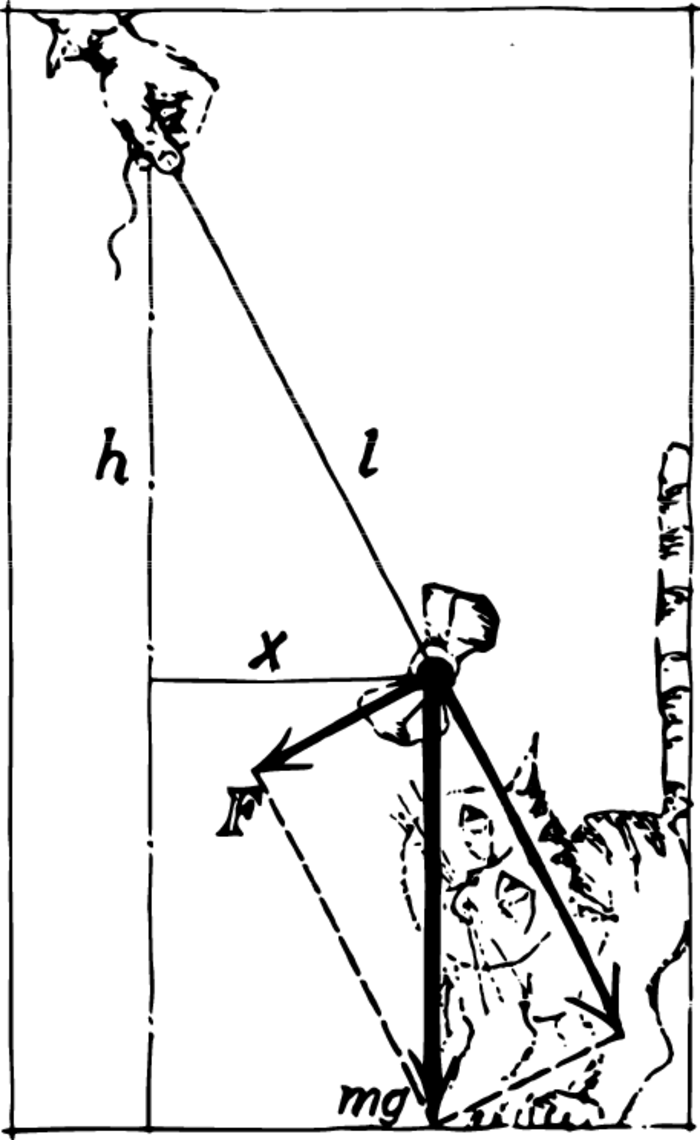
Denote the magnitude of the displacement of the bob by \(x\). The motion takes place along an arc, but we have agreed to investigate oscillations near an equilibrium position. We therefore make no distinction between the magnitude of a displacement along the arc and the deviation of the bob from the vertical. Let us consider two similar triangles. The ratio of the corresponding legs is equal to the ratio of the hypotenuses, i.e. \[\frac{F}{x} = \frac{mg}{l}, \,\,\textrm{or}\,\,F = \frac{mg}{l}x\] The quantity \(mg/l\) does not change during the oscillation. If we denote this constant by \(k\), then the restoring force \(F\) is given by the formula \(F = kx\). We arrive at the following conclusion: the magnitude of the restoring force is directly proportional to that of the displacement of an oscillating point from its equilibrium position. The restoring force is maximum at the extreme positions of a vibrating body. When the body passes through the midpoint, the force vanishes and changes sign or, in other words, direction. While the body is displaced to the right, the force is directed to the left, and conversely.

The pendulum serves as the simplest example of an oscillating body. However, we are interested in the possibility of extending the formulas and laws which we find to arbitrary vibrations.

The period of oscillation of a pendulum was expressed in terms of its length. Such a formula applies only to a pendulum. But we can express the period of free oscillations in terms of the restoring force constant \(k\). Since \(k = mg/l\), we have \(l/g= m/k\), and so \[T = 2 \pi \sqrt{\frac{m}{k}}\] This formula extends to all cases of oscillations, since any free oscillation takes place under the action of a restoring force.

Let us now express the potential energy of a pendulum in terms of its displacement \(x\) from the equilibrium position. We may take the potential energy of the bob to be zero when it passes through the lowest point, and then the height of its ascent should be measured from this point. Denoting the difference in height between the point of suspension and the level of the deflected bob by \(h\), we express the potential energy as follows: \(U = mg (l - h)\) or, using the formula for the difference of squares, \[U = mg \frac{l^{2}-h^{2}}{l+h}\] But, as can be seen from the figure, \(l^{2} -h^{2} = x^{2}\), \(l\) and \(h\) differ very slightly and, therefore, \(2l\) may be substituted for \(l + h\). Thus, \(U = mgx^{2}/2l\) \[U = \frac{kx^{2}}{2}\] The potential energy of an oscillating body is proportional to the square of its displacement from the equilibrium position.

Let us check the correctness of the formula we have just derived. The loss of potential energy must be equal to the work performed by the restoring force. Consider two of the body’s positions, \(x_{2}\) and \(x_{1}\). The difference in potential energy \[U_{2} - U_{1} = \frac{k x_{2}^{2}}{2} - \frac{k x_{1}^{2}}{2} = \frac{k}{2} \left(x_{2}^{2} - x_{1}^{2} \right)\] But a difference of squares may be written as the product of the sum by the difference. Hence, \[U_{2} - U_{1} = \frac{k}{2} (x_{2} + x_{1})(x_{2} - x_{1}) = \frac{kx_{2}+kx_{1}}{2} (x_{2}-x_{1})\] \(x_{2}-x_{1}\) is the length of the path covered by the body, and \(kx_{1}\) and \(kx_{2}\) are the magnitudes of the restoring force at the beginning and end of the motion, and \((kx_{1}+kx_{2})/2\) is equal to the average force.

Our formula led us to the correct result: the loss of potential energy is equal to the work performed.