Let us attach a piece of soft lead to the bob of a pendulum and hang the pendulum over a sheet of paper in such a way that the lead touches the paper (Figure 1).

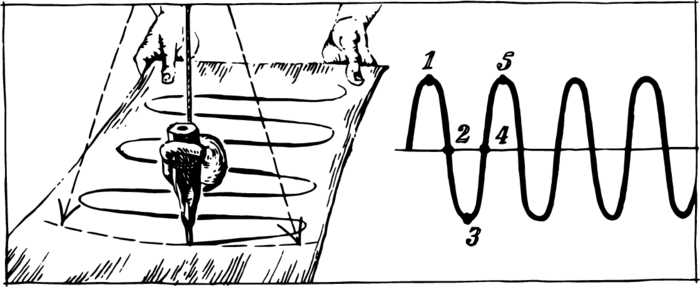
Now we deflect the pendulum slightly. The oscillating lead will trace a small line segment on the paper. At the midpoint of the oscillation, when the pendulum is passing through its equilibrium position, the pencil line will be thicker, since in this position the lead presses down harder on the paper. If we pull the sheet of paper in the direction perpendicular to the plane of the oscillation, the curve depicted in Figure 1 will be traced. It is not difficult to see that the wavelets so obtained will be dense if the paper is pulled slowly, and sparse if the sheet of paper moves with a considerable speed. In order for the curve to turn out accurate, it is necessary that the sheet of paper move uniformly.

In this manner we have in a sense “displayed” the oscillations.

The display is needed in order to say where the bob of the pendulum was located and where it was moving at one or another instant. Imagine that the paper moves with a speed of \(1\,\mathrm{cm/s}\) from the time when the pendulum was as far as possible from, say, to the left of, the midpoint. This initial position corresponds to the point on our graph which has been marked with the number 1.

After a quarter of the period the pendulum will pass through the midpoint. During this time the paper has moved \(T/4\) centimetres (point 2 in the figure). The pendulum now moves to the right and the paper simultaneously crawls along. When the pendulum comes to its extreme right position, the paper will have moved \(T/2\) centimetres (point 3 in the figure). The pendulum again moves towards the midpoint and arrives at its equilibrium position in \(3T/4\) (point 4 in the diagram). Point 5 finishes a complete oscillation, after which the motion is repeated every \(T\) seconds or every \(T\) centimetres on our graph.

Thus, a vertical line on the graph is the scale of the displacement of a point from the equilibrium position, and the central horizontal line is the time scale.

The two quantities which characterize an oscillation in an exhaustive manner are easily found from such a graph. The period can be determined by the distance between two equivalent points, for example, between two neighbouring summits. The maximum displacement of a point from the equilibrium position can also be measured at once. This displacement is called the amplitude of the oscillation.

Displaying an oscillation permits us, moreover, to answer the question posed above: Where is an oscillating point at one or another instant? For example, where will an oscillating point be in 11 seconds if the period of oscillation is equal to 3 seconds and the motion began at the extreme left position? The oscillation begins from the very same point in every 3 seconds. Therefore, in 9 seconds the body will also be at the extreme left position.

Consequently, there is no need of a graph in which the curve is extended over several periods; a graph depicting the curve corresponding to one oscillation is quite enough. In 11 seconds the state of an oscillating point will be the same as in 2 seconds if the period is 3 seconds. Laying off 2 centimetres in our diagram (for we stipulated that the paper be pulled with a speed of \(1\,\mathrm{cm/s}\) or, in other words, that the scale of our diagram be 1 second to 1 centimetre), we see that in 11 seconds the point will be on its way from the extreme right position to that of equilibrium. The magnitude of the displacement at this instant can be found from the figure.

It isn’t necessary to turn to a graph in order to find the magnitude of the displacement of a point making small oscillations about its equilibrium position. Theory shows that in this case the curve depicting the dependence of the displacement on the time is a sinusoid. If we denote the displacement of a point by \(y\), the amplitude by \(a\), and the period of the oscillation by \(T\), we can find the magnitude of the displacement at a time \(t\) after the beginning of the oscillation by means of the formula: \[A = a \sin 2 \pi \frac{t}{T}\] An oscillation taking place in accordance with this law is called harmonic. The argument of the sine is equal to the product of \(2\pi\) by \(t/T\). The quantity \(2 \pi t/T\) is called the phase.

Having trigonometric tables at hand and knowing the period and amplitude, we can easily compute the magnitude of the displacement of a point, and figure out on the basis of the value of the phase in which direction it is moving.

It is not difficult to derive the formula for vibratory motion by considering the motion of the shadow cast on a wall by a bob moving around a circle (Figure 2).

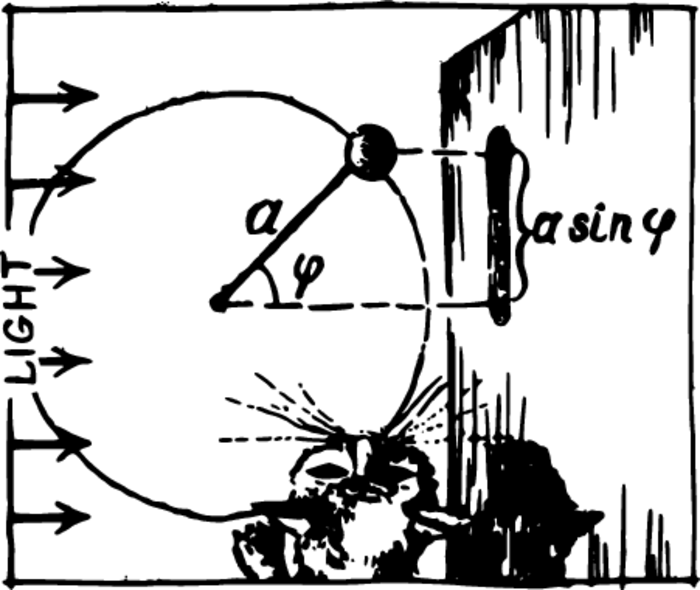
We shall mark off the displacements of the shadow from its central position. At the extreme positions the displacement \(y\) is equal to the radius \(a\) of the circle. This is the amplitude of the oscillation of the shadow.

If the bob has moved along the circle through an angle \(\varphi\) from the central position, its shadow will deviate from the midpoint by \(a \sin (\varphi)\).

Let the period of the motion of the bob (which, of course, is also the period of oscillation of the shadow) be \(T\); this means that the bob passes through \(2\pi\) radians during the time \(T\). We may form the proportion \(\varphi/t = 2\pi/T\), where \(t\) is the time required for a revolution through an angle \(\varphi\).

Consequently, \(\varphi = 2\pi t /T\) and \(y = a \sin 2 \pi t/T\). This is precisely what we wished to prove.

The velocity of an oscillating point also changes according to a sinusoidal law. The same kind of reasoning about the movement of the shadow of a bob describing a circle will lead us to this conclusion. The velocity of the bob is a vector of constant length \(v_{0}\). The velocity vector revolves together with the bob. Let us think of the velocity vector as a physical arrow capable of casting a shadow. At the extreme positions of the bob, the vector will lie along a ray of light and will not create a shadow.

When the bob moves around the circle from an extreme position through an angle \(\theta\), the vector velocity will turn through the same angle and its projection will be equal to \(v_{0} \sin \theta\). But on the same basis as before, \(\theta /t = 2\pi/T\) and so the instantaneous speed of the vibrating body \[v = v_{0} \sin \frac{2\pi}{T} t\] Note that in the formula for determining the magnitude of the displacement, the time is equal to zero at the central position, and in the formula for the speed at the extreme positions. The displacement of a pendulum equals zero when the bob is at the central position, and the speed of oscillation is zero at the extreme positions.

There is a simple relation between the maximum speed \(v_{0}\) of an oscillation and the maximum displacement (or amplitude): the bob describes a circle with a circumference \(2 \pi a\) during the period \(T\) of the oscillation. Therefore, \[v_{0} = \frac{2\pi a}{T} \,\,\textrm{and}\,\,v=\frac{2 \pi a}{T} \sin \frac{2 \pi}{T} t\]