Try to get a heavy flywheel rotating by hand. Pull one of the spokes. You will find it difficult if you grasp it too near to the axle. Move your hand towards the rim, and thing’s will become easier.
But what has chanced? After all, the force is the same in both cases. The point of application of the force has changed.
In all that preceded, the question of where a force is applied did not arise, since the form and size of a body played no role in the problems under consideration. What we essentially did was to conceptually replace a body by a point.
The example with the rotation of a wheel shows that the question of the point of application of a force is far from idle when we are dealing with the rotation or revolution of a body.
In order to understand the role of the point of application of a force, let us compute the work which must be performed to turn a body through a certain angle. In this calculation, of course, it is assumed that all the particles of the body are rigidly bound to one another (we are ignoring at present the ability of a body to bend, contract and, in general, to change its form). Therefore, a force applied to one point of a body imparts kinetic energy to all its parts.
In computing this work, the role of the point of application of a force is clearly seen. A body fastened to an axis is shown in Figure 1. When the body turns through a small angle \(\varphi\), the point of application of a force moves along an arc—it is displaced by a distance \(s\).
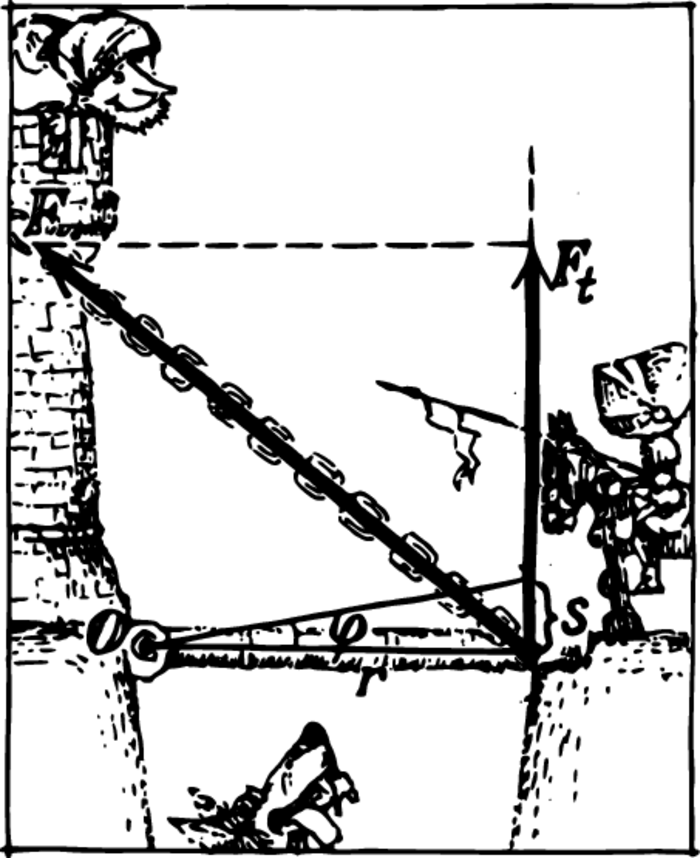
Projecting the force onto the direction of the motion, i.e. onto the tangent to the circle around which the point of application moves, we find a familiar expression for the work \(W\): \[W = F_{t} \, s\] But the arc \(s\) may be represented as follows: \[s = r \, \varphi\] where \(r\) is the distance from the axis of rotation to the point of application of the force. Thus, \[W = F_{t} \, r \varphi\] Turning the body through one and the same angle in various ways, we may expend different amounts of work depending on where the force is applied.
If the angle is given, the work is determined by the product \(F_{t}r\). This product is called the moment of force, or the torque: \[M = F_{t} \, r\] Our formula for the torque can be given another form. Let \(O\) be the axis of rotation, and \(B\) the point of application of the force Figure 2. The length of the perpendicular dropped from \(O\) to the direction of the force is denoted by \(d\). The two triangles constructed in the figure are similar. Therefore, \[\dfrac{F}{F_{t}} = \dfrac{r}{d} \quad \textrm{or} \quad F_{t} \, r = F \, d\] The quantity \(d\) is called the arm, or the lever arm, of the force.
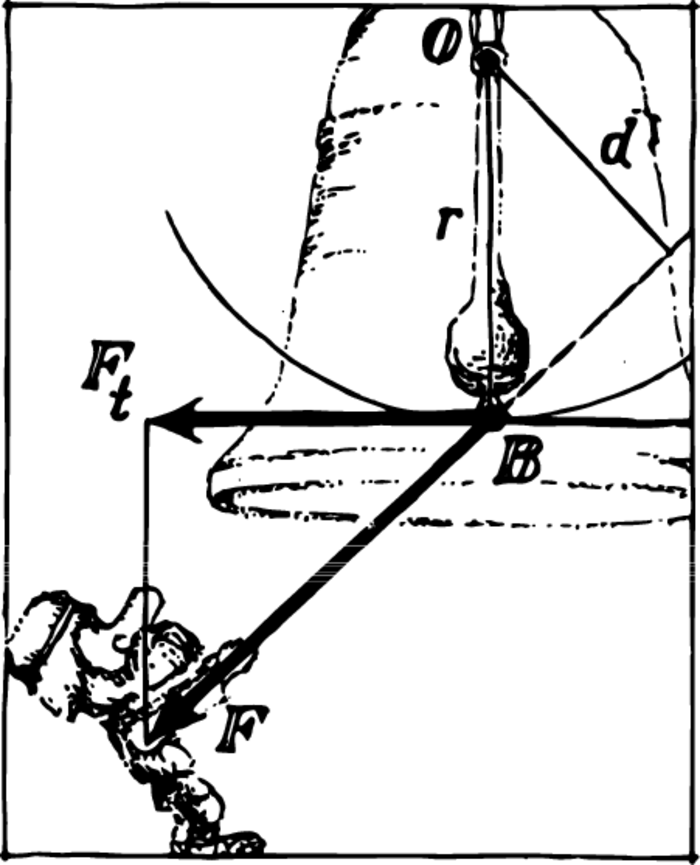
Our new formula \(M = F \, d\) reads as follows: the torque is equal to the product of the force by its lever arm.
If we displace the point of application of the force along its direction, then the lever arm \(d\) and with it the torque \(M\) will not be changed. Hence, it makes no difference just where the point of application lies on the line of action of the force.
With the aid of the new concept, the formula for the work can be written out more concisely. \[W = M \varphi\] i.e. the work is equal to the product of the torque by the angle of rotation.
Let two forces act on a body with moments \(M_{1}\) and \(M_{2}\). When the body is rotated through an angle \(\varphi\) the work done will be \[M_{1}\varphi + M_{2}\varphi = (M_{1} + M_{2})\, \varphi\] This equality shows that two forces with moments \(M_{1}\) and \(M_{2}\) rotate a body just as a single force with moment \(M = M_{1} + M_{2}\) would. Moments of force can help, as well as hinder, each other. If torques \(M_{1}\) and \(M_{2}\) tend to rotate a body in one and the same direction, we should regard them as magnitudes having the same sign. On the contrary, torques rotating a body in opposite directions have different signs.
As we know, the work done by all the forces acting on a body effects a change in its kinetic energy.
The rotation of a body slowed down or speeded up, hence, its kinetic energy changed. This can only take place in case the resultant torque is not equal to zero.
And what if the resultant torque is equal to zero? The answer is obvious—the kinetic energy does not change; consequently, the body either rotates uniformly by inertia or remains stationary
Thus, the equilibrium of a body capable of rotating requires the balancing of all the torques acting on it. If there are two such torques, the equilibrium requires that \[M_{1} + M_{2} = 0\] While we were interested in problems in which a body could be regarded as a point, the conditions for equilibrium were simple: in order for a body to remain stationary or move uniformly, stated Newton’s law for such problems, it is necessary that the resultant force be equal to zero; the forces acting upwards must balance those directed downwards; the rightward force must compensate for the leftward one.
This law is also valid for our case. If a flywheel is stationary, the forces acting on it are balanced by the reaction of the axle around which the wheel can turn.
But these necessary conditions become insufficient. Besides the balancing of forces, the balancing of torques is also required. The balancing of moments of force is the second necessary condition for the rest or uniform rotation of a solid body.
Torques, if there are several of them, can be easily separated into two groups: some tend to rotate a body clockwise, and others counterclockwise. These are precisely the moments of force which must compensate for each other.