While solving mechanical problems in which a body was conceptually replaced by a point, the question of how to add forces was answered simply on the preceding pages. The parallelogram law of forces yielded an answer to this question, and if the forces were parallel, we added their magnitudes like numbers.

Now matters are more complicated. For the effect of a force on an object is characterized not only by its magnitude and direction but also by the point of its application, or—we have explained above that this is the same thing—its line of action.

To add forces means to replace them by a single force. This is by no means always possible.

The replacement of parallel forces by a single resultant is a problem which can always be solved (except in a special case, which will be discussed at the end of this section). Let us consider the addition of parallel forces. Of course, the sum of forces of \(3\,\mathrm{kgf}\) and \(5\,\mathrm{kgf}\) is equal to \(8\,\mathrm{kgf}\), provided that they have the same direction. The problem consists in finding the point of application (line of action) of the resultant force.

Two forces acting on a body are depicted in Figure 2. The resultant force \(F\) replaces the forces \(F_{1}\) and \(F_{2}\), but this means not only that \(F = F_{1} +F_{2}\); the action of \(F\) will be equivalent to that of \(F_{1}\) and \(F_{2}\) in case the torque produced by \(F\) is equal to the sum of the torques produced by \(F_{1}\) and \(F_{2}\). We are looking for the line of action of the resultant force \(F\). Of course, it is parallel to the forces \(F_{1}\) and \(F_{2}\), but how far is this line from \(F_{1}\) and \(F_{2}\)?

A point lying on the segment joining the points of application of \(F_{1}\) and \(F_{2}\) is depicted in the figure as \(F\)’s point of application. With respect to the chosen point, the moment of \(F\) is, of course, equal to zero. But then the sum of the moments of \(F_{1}\) and \(F_{2}\) with respect to this point should also be equal to zero, i.e. the torques produced by \(F_{1}\) and \(F_{2}\) opposite in sign will be equal in magnitude.

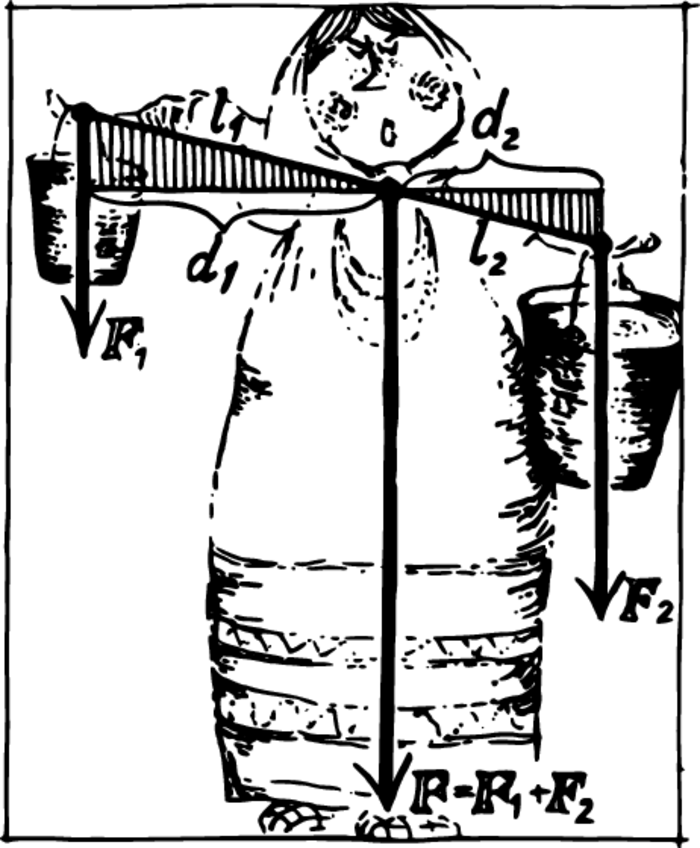
Denoting the lever arms of \(F_{1}\) and \(F_{2}\) by \(d_{1}\) and \(d_{2}\) , we may write out this condition as follows: \[F_{1} d_{1} = F_{2} d_{2} \quad \textrm{or} \quad \dfrac{F_{1}}{F_{2}} = \dfrac{d_{2}}{d_{1}}\] It follows from the similarity of the shaded triangles that \(d_{2}/d_{1} = l_{2}/l_{1}\) i.e. the point of application of the resultant force divides the distance on the uniting segment between the added forces into parts, \(l_{1}\) and \(l_{2}\) which are inversely proportional to the forces.

Denote the distance between the points of application of \(F_{1}\) and \(F_{2}\) by \(l\). It is obvious that \(l = l_{1} + l_{2}\).

Let us solve the following system of two equations in two variables \begin{align} F_{1} l_{1} - F_{2} l_{2} & = 0 \\ l_{1} + l_{2} & = l \end{align} We obtain \[l_{1} = \dfrac{F_{2} l}{F_{1} + F_{2}}, \quad l_{2} = \dfrac{F_{1}l}{F_{1} + F_{2}}\] By means of these formulas, we can find the point of application of the resultant force not only in the case when the forces have the same direction but also in the case of the forces with opposite directions (antiparallel forces, as we say). If the forces have different directions, they have opposite signs, and the resultant is equal to the difference \(F_{1} - F_{2}\) of the forces and not to their sum. Taking the smaller of the two forces, \(F_{2}\), to be negative, we see by our formulas that \(l_{2}\) becomes negative. This means that the point of application of \(F_{1}\) lies not to the left (as before) but to the right of the point of application of the resultant force Figure 2; moreover, as in the previous case, \[\dfrac{F_{1}}{F_{2}} = \dfrac{l_{2}}{l_{1}}\] An interesting result is obtained for equal antiparallel forces. Then \(F_{1} + F_{2} = 0\). The formulas show that \(l_{1}\) and \(l_{2}\) will then become infinitely large. What is the physical meaning of this assertion? Since it is meaningless to put the resultant at infinity, it is therefore impossible to replace equal antiparallel forces by a single force.

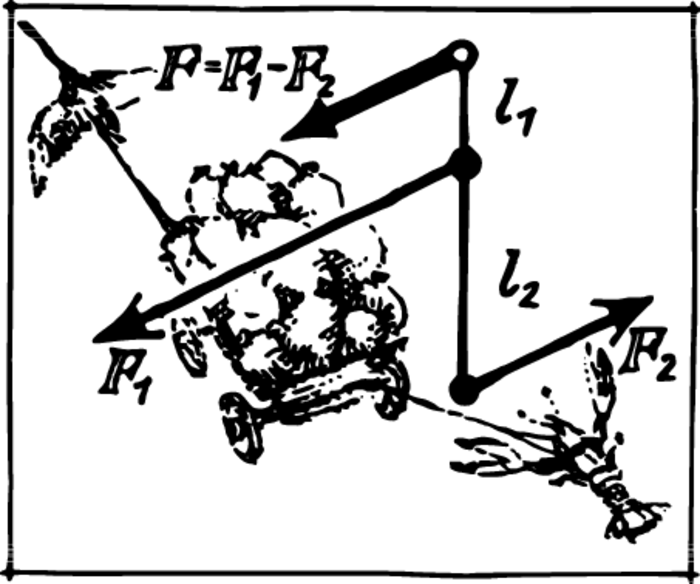
Such a combination of forces is called a couple.

The action of a couple cannot be reduced to the action of one force. Any other pair of parallel or antiparallel forces can be balanced by a single force, but a couple cannot.

Of course, it would be false to say that the forces constituting a couple cancel each other. A couple has quite a significant effect—it rotates a body; the peculiarity of the action of a couple consists in the fact that it does not produce a translational motion.

In certain cases, the question may arise not of adding parallel forces but of decomposing a given force into two parallel ones.

Two persons carrying a heavy basket together on a pole are depicted in Figure 3. The weight of the basket is distributed between the two of them. If the load presses down on the centre of the pole, they both feel the same weight. If the distances from the point of application of the load to the hands which carry it are \(d_{1}\) and \(d_{2}\), the force \(F\) is decomposed into forces \(F_{1}\) and \(F_{2}\) according to the rule \[\dfrac{F_{1}}{F_{2}} = \dfrac{d_{2}}{d_{1}}\] The stronger person should take hold of the pole nearer to the load.