All particles of a body possess weight. Therefore, a solid body is subject to the action of an infinite number of gravitational forces. Moreover, all these forces are parallel. If so, it is possible to add them according to the rules which we have just considered and replace them by a single force. The point of application of the resultant force is called the centre of gravity. It is as if the weight of a body were concentrated at this point.

Let us suspend a body by one of its points. How will it then be situated? Since we may conceptually replace the body by one load concentrated at the centre of gravity, it is clear that in equilibrium this load will lie on the vertical passing through the pivot. In other words, in equilibrium the centre of gravity lies on the vertical passing through the pivot, and is at its lowest possible position.

One can place the centre of gravity on the vertical passing through the axis and above the pivot. It will be very difficult to do this and only because of the presence of friction. Such an equilibrium is unstable. We have already discussed the condition for stable equilibrium—the potential energy must be minimum. This is precisely the case when the centre of gravity lies below the pivot. Any deflection raises the centre of gravity and, therefore, increases the potential energy. On the contrary, when the centre of gravity lies above the pivot, any puff removing the body from this position leads to a decrease in potential energy. Such a position is unstable.

Cut a figure out of cardboard. In order to find its centre of gravity, hang it up twice, attaching the suspending thread first to one and then to another point of the body. Attach the figure to an axis passing through its centre of gravity. Turn the figure to one position, a second, a third, … We observe the complete neutrality of the body towards our operations. A special case of equilibrium is attained in any position. This is just what we call it—neutral.

The reason for this is clear—in any position of the figure, the material point replacing it is located at one and the same place.

In a number of cases, the centre of gravity can be found without any experiments or computations. It is clear, for example, that the centres of gravity of a sphere, circle, square and rectangle are located at the centres of these figures, since they are symmetrical. If we conceptually break up a symmetrical body into small parts, each of them will correspond to another located symmetrically on the other side of the centre. And for each pair of such particles, the centre of the figure will be the centre of gravity.

The centre of gravity of a triangle lies at the intersection of its medians. In fact, let us break up a triangle into narrow strips parallel to one of the sides. A median divides each of the strips in half. But the centre of gravity of a strip lies, of course, half-way along it, i.e. on the median. The centres of gravity of all the strips occur on the median, and when we add their weights, we arrive at the conclusion that the centre of gravity of the triangle lies somewhere on the median. But this argument is valid with respect to any of the medians. Therefore, the centre of gravity must lie at their intersection.

But perhaps you are not convinced that the three medians intersect in a single point. This is proved in geometry; but our argument also proves this interesting theorem. For a body cannot have several centres of gravity; but since the centre of gravity is one and lies on a median, no matter from which vertex we draw it, all the three medians therefore intersect in a single point. The formulation of a physical problem helped us prove a geometric theorem.

It is more difficult to find the centre of gravity of a homogeneous cone. It is only clear from considerations of symmetry that the centre of gravity lies on the axis. Computations show that it is located at the distance of a quarter of the height from the base.

The centre of gravity is not necessarily located inside a body. For example, the centre of gravity of a ring is located at its centre, i.e. outside the ring.

Can a pin be placed in a vertical position on a glass pedestal and stay stable?

It is shown in Figure 1 how to do this. A small apparatus consisting of wires in the form of a double yoke with four small loads should be rigidly fastened to the pin. Since the loads are hanging lower down than the pivot, and the weight of the pin is small, the centre of gravity lies below the pivot. The position is stable.

So far we have been dealing with bodies possessing a point of support. What is the situation in those cases when a body is supported over an entire area element?

It is clear that in this case the location of the centre of gravity above the support does not at all imply that the equilibrium is unstable. How else could glasses stand on a table? It is necessary for stability that the line of action of the gravitational force drawn from the centre of gravity pass through the area of support. On the contrary, if the line of action passes outside the area of support, the body will fall.

Stability may differ greatly depending on how high above the support the centre of gravity is. Only a very clumsy person will overturn a glass of teal but a flower vase with a small base can be overturned by a careless touch. What is the point here?

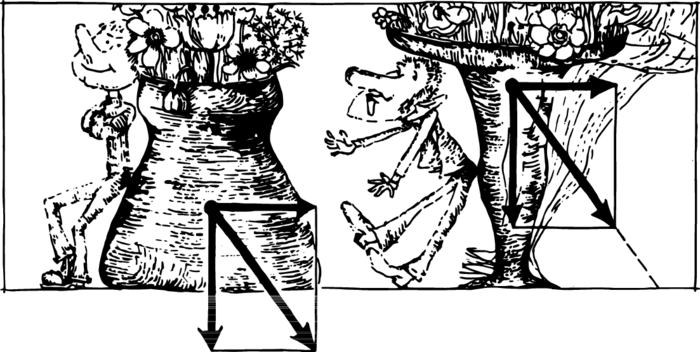
Take a look at Figure 2. Identical horizontal forces are applied to the centres of gravity of two vases. The vase at the right will overturn, since the resultant force doesn’t pass through its base but is directed to one side.

We have said that for a body to be stable, the force applied to it must pass through the area of support. But the area of support needed for equilibrium does not always correspond to the actual area of support. A body whose area of support has the form of a crescent is depicted in Figure 3. It is easy to see that the stability of the body will not change if the crescent is completed to a solid half-disc. Thus, the area of support determining the condition for equilibrium may be greater than the actual one.

In order to find the area of support for the tripod depicted in Figure 4, one must join its tips with straight-line segments.

Why is it so hard to walk a tightrope? Because the area of support has sharply decreased. It isn’t easy to walk a tightrope, and skilful tightrope walkers aren’t rewarded with applause for nothing. However, sometimes viewers make the mistake of acclaiming clever tricks simplifying the task as the epitome of artistry. The performer takes a heavily bent yoke with two pails of water; the pails turn out to be on the level of the tightrope. With a straight face, while the orchestra has ceased playing, the performer takes his walk along the tightrope. How complicated has the trick become, thinks the inexperienced viewer. As a matter of fact, the performer has simplified his task by lowering the centre of gravity.