So far we have been dealing with the magnitude of angular momentum. But angular momentum has the properties of a vector.

Consider the rotation of a point with respect to some “centre”. Two nearby positions of the point are depicted in illustration below Figure 1. The motion in which we are interested is characterized by the magnitude of its angular momentum and the plane in which it takes place. The plane of the motion is shaded in the figure—it is the area swept out by the radius drawn from the “centre” to the moving point.

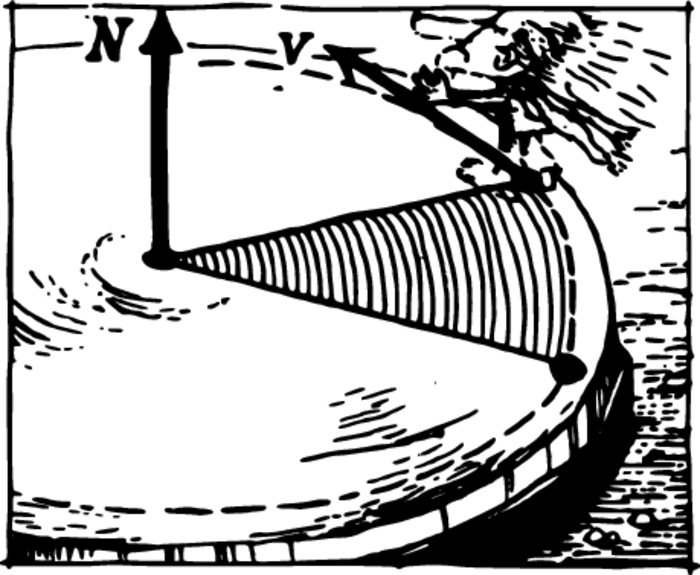
Information about the direction of the plane of the motion and about the magnitude of the angular momentum can be combined. The angular momentum vector, directed along the normal to the plane of motion and equal in magnitude to the absolute value of the angular momentum, serves for this purpose. However, this is still not all—one must take into account the direction of the motion in the plane: for a body can rotate about a centre in the clockwise as well as in the counterclockwise direction.

It is customary to draw an angular momentum vector in such a manner that we see the point rotating in the counterclockwise direction when we look at it facing the vector. This can also be said otherwise: the direction of the angular momentum vector is related to the direction of the rotation in the same way as the direction of a turning corkscrew is related to the direction of the motion of its handle.

Thus, if we know the angular momentum vector, we can determine the magnitude of the angular momentum, the position of the plane of motion in space, and the direction of the rotation with respect to the “centre”.

If the motion takes place in one and the same plane, and the lever arm and speed change, the angular momentum vector preserves its direction in space, but changes in length. And in the case of an arbitrary motion, the angular momentum vector changes both in direction and in magnitude. It may seem that such a fusion into one concept of the direction of the plane of motion and the magnitude of an angular momentum serves only the purpose of saving words. In reality, however, when we are dealing with a system of bodies moving in more than one plane, we obtain the law of conservation of angular momentum only when we add moments of momentum as vectors. This circumstance shows that the attribution of a vector nature to angular momentum has a profound content.

Angular momentum is always defined with respect to some conditionally chosen “centre”. It is only natural that this quantity depends, generally speaking, on the choice of this point. Nevertheless, it can be shown that if the system of bodies under consideration is stationary on the whole (its total momentum is equal to zero), its angular momentum vector is independent of our choice of “centre” This angular momentum may be called the internal angular momentum of the system of bodies.

The law of conservation of angular momentum vector is the third and last conservation law in mechanics. However, we are not being entirely precise when speaking of three conservation laws. In fact, momentum and angular momentum are vector quantities, and a law of conservation of a vector quantity implies that not only its magnitude remains constant but also its direction. To put it otherwise, the three components of a vector in three mutually perpendicular directions in space remain constant. Energy is a scalar quantity, momentum is a vector quantity, and angular momentum is also a vector quantity. It would therefore be more precise to say that seven conservation laws hold in mechanics.