We shall now become acquainted with another mechanical concept, which permits us to formulate a new important law of motion. This concept is called angular momentum, or moment of momentum. The very names suggest that we are dealing with the quantity which somehow resembles a moment of force.

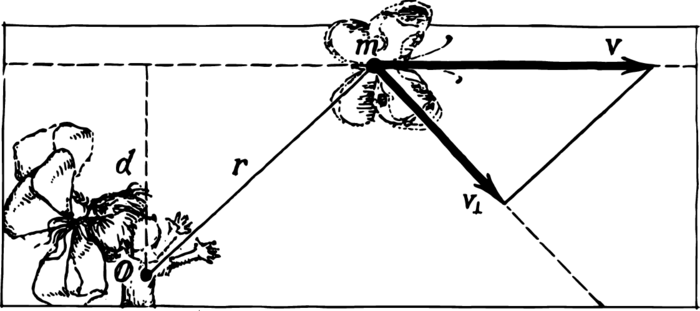
A moment of momentum, just as a moment of force, requires the indication of the point with respect to which the moment is defined. In order to define the angular momentum relative to some point, one must construct the momentum vector and drop a perpendicular from the point to its direction. The product of the momentum \(m \, v\) by the lever arm \(d\) is precisely the angular momentum, which we shall denote by the letter \(N\): \[N = m \, v d\] If a body is moving freely, its velocity does not change, the lever arm with respect to any point also remains constant, since the motion takes place along a straight line. Consequently, the angular momentum also remains constant during such a motion.

Just as for the moment of force, we can also obtain a different formula for the moment of momentum. Draw a radius between the position of the body and the point with respect to which we are interested in the angular momentum Figure 1. Construct also the projection of the velocity onto the direction perpendicular to the radius. It follows from the similar triangles constructed in the figure that \(v/v_{\perp} = r/d\). Therefore, \(vd = v_{\perp}r\), and the formula for angular momentum may also be written in the following form: \[N = m \, v_{\perp}r\]

During free motion, as we have just said, angular momentum remains constant. Well, but if a force is acting on the body? Computations show that the change in angular momentum during a second is equal to the torque. This law can be extended without difficulty to systems of bodies. If we add the changes in the angular momenta of all the bodies belonging to the system in a unit of time, their sum turns out to be equal to the sum of the torques acting on the bodies. Consequently, the following statement is valid for a group of bodies: the change in the total moment of momentum in a unit of time is equal to the sum of the moments of all the forces.