People have been solving the problem of throwing an object as far as possible from time immemorial. A stone thrown by hand or shot from a sling, an arrow flown from a bow, a rifle bullet, an artillery shell, a ballistic missile—here is a brief list of successes in this field.

The thrown object will move in a curved line called a parabola. It can be constructed without difficulty if we regard the motion of a thrown body as the sum of two motions—horizontal and vertical—taking place simultaneously and independently. The acceleration of free fall is vertical, and so a flying bullet moves horizontally by inertia with a constant velocity and simultaneously falls to the Earth vertically with a constant acceleration. But how can we add these two motions?

Let us begin with a simple case—when the initial velocity is horizontal (say, we are dealing with a shot from a rifle whose barrel is horizontal). Take a sheet of graph paper and draw a vertical and a horizontal lines (Figure 1). Since the two motions are taking place independently, in \(t\) seconds the body is displaced by an interval of \(v_{0}t\) to the right and an interval of \(gt^{2} /2\) downwards. Mark off the segment \(v_{0}t\) along the horizontal line, and from its end point, the vertical segment \(gt^{2} /2\). The end point of the vertical segment represents the point where the body will be in \(t\) seconds. This construction must be carried out for several points, i.e. for several instants of time. A smooth curve—the parabola representing the trajectory of the body—will pass through these points. The more frequently one lays off these points, the more accurately will the trajectory of the flight of the bullet be constructed.

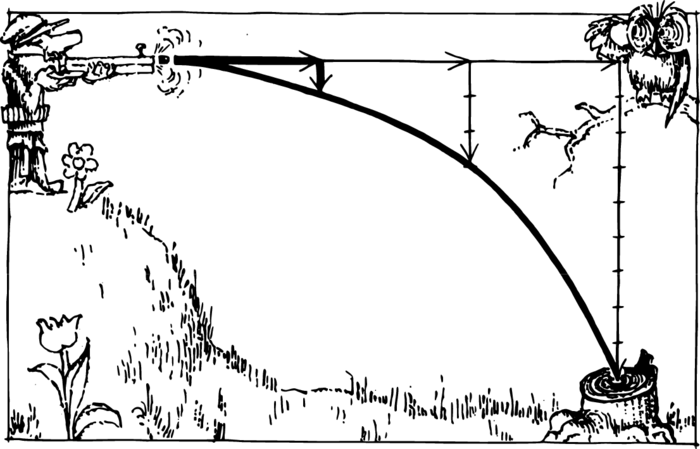
A trajectory has been constructed in Figure 2 for the case when the initial velocity \(v_{0}\) is directed at an angle. The vector \(v_{0}\) should first of all be decomposed into its vertical and horizontal components. On the horizontal line we mark off \(v_{\textrm{hor}} t\)—the distance through which the bullet will move horizontally in \(t\) seconds.

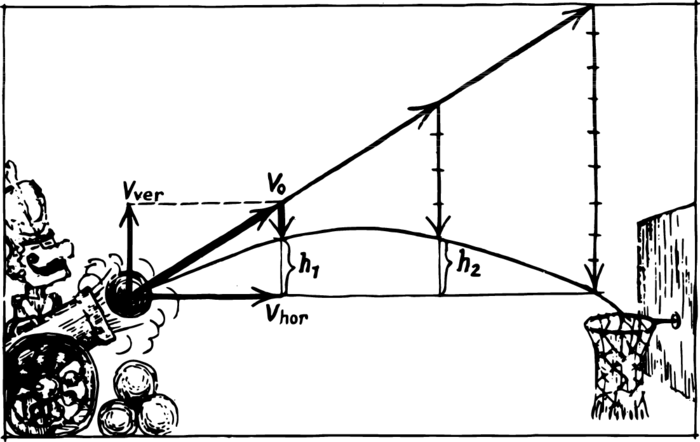
But the bullet simultaneously performs an upward motion. In \(t\) seconds it will rise to a height of \(h = v_{\textrm{ver}} t - gt^{2} /2\). By means of this formula, substituting in it the instants of time of interest to us, we can compute the vertical displacements and mark them off on the vertical axis. The values of \(h\) will first increase (rise) and then decrease.

It now remains to mark the points of the trajectory on the graph, just as we did in the preceding example, and draw a smooth curve through them.

If the rifle barrel is held horizontally, the bullet will soon burrow into the ground; if the barrel is vertical, it will fall at the place where the shot was fired. Therefore, in order to shoot as far as possible, one must fix the barrel of the rifle at some angle to the horizontal. But at what angle?

Let us again employ the same device—decompose the initial velocity vector into its two components: a vertical vector equal to \(v_{1}\) and a horizontal vector to \(v_{2}\). The time between the moment the shot is fired until the moment the bullet reaches its highest point is equal to \(v_{1}/ g\). Note that the bullet will be falling downwards for the same length of time, i.e. the complete time of the flight of the bullet until it lands on the ground is \(2v_{1}/g\).

Since the horizontal motion is uniform, the range of the flight is equal to \[s = \frac{2v_{1}v_{2}}{g}\] (we have ignored the height of the rifle above ground level in our calculation).

We have obtained a formula which shows that the range of the flight is proportional to the product of the velocity components. For what firing direction will this product be greatest? This question can be expressed by means of the geometrical rule of the addition of vectors. The velocities \(v_{1}\) and \(v_{2}\) form the sides of the velocity rectangle; a diagonal in it is the total velocity \(v\). The product \(v_{1}v_{2}\) is equal to the area of this rectangle.

Our question reduces to the following: Given the length of a diagonal, what sides must be taken for the area of the rectangle to be maximum? It is proved in geometry that this condition is satisfied by a square. Therefore, the range of the flight of the bullet will be greatest when \(v_{1} = v_{2}\) , i.e. when the velocity rectangle reduces to a square. A diagonal of the velocity square forms an angle of 45° with the horizontal—this is precisely the angle at which the rifle must be held for the bullet to fly as far as possible.

If \(v\) is the total velocity of the bullet, then in the case 2. The range-of-flight of a square we have \(v_{1} = v_{2} =v\sqrt{2}\) formula for this optimal case looks as follows: \(s = v^{2}/g\), i.e. the range will be twice as great as the maximum height of a bullet fired upwards with the same initial speed.

The maximum height of a bullet fired at an angle of 45° will be \(h = v_{1}^{2}/2g = v^{2}/4g\), i.e. four times less than the range of flight.

It should be admitted that the formulas we have been applying yield exact results only in the case, quite remote from practice, when air is absent. In many cases air resistance plays a decisive role and radically changes the entire picture.