Let us now deal with rotating systems. The motion of such a system is determined by the number of revolutions per second which it makes about an axis. It is also necessary, of course, to know the direction of the axis of rotation.

In order to better understand the peculiarities of life in rotating systems, let us consider the “wheel of laughs” – a well-known ride. Its construction is rather simple. A smooth disc, several metres in diameter, rotates rapidly. Those who so desire are invited to get on it and to try to keep their balance. Even people who know no physics quickly acquire the secret of success: one must go to the centre of the disc, since the farther one is from the centre, the more difficult it is to keep one’s balance.

Such a disc is a non-inertial frame of reference with several special features. Every object attached to the disc moves around a circle of radius \(R\) with speed \(v\), i.e. with acceleration \(v^{2}/R\). As we already know, from the point of view of a non-inertial observer this implies the presence of an additional force \(mv^{2}/R\) directed along the radius outwards from the centre. This radial force will act at each point of the “devilish wheel” creating there a radial acceleration \(v^{2}/R\). The magnitude of this acceleration will be identical for points lying on the same circle. And what about points on different circles? Don’t rush to answer that according to the formula \(v^{2}/R\) the smaller the distance from the centre, the greater will be the acceleration. This isn’t true because the speed of points farther from the centre of the wheel will be greater. In fact, if the wheel makes \(n\) revolutions per second, the path traversed by a point on the rim of the wheel in one second (the speed of this point) is \(2\pi R n\).

The speed of a point is directly proportional to its distance from the centre. We may now rewrite our formula for the acceleration: \[a = 4 \pi^{2} n^{2} R\] Since the number of revolutions made in a second is the same for all points of the wheel, we arrive at the following result: the acceleration due to the force exerted by the “radial gravity” acting on a rotating wheel grows in proportion to the distance of a point from the centre of the wheel.

In this interesting non-inertial frame of reference the force of gravity is different on different circles. Therefore, the directions of the “verticals” will also be different for bodies located at different distances from the centre. The Earth’s gravitational force is, of course, the same at all points of the wheel. But the vector characterizing the additional radial force becomes longer as the distance from the centre increases. Therefore, the diagonals of the rectangles deviate more and more from the vertical (normal to the Earth’s surface).

If we imagine the successive sensations of a person slipping off the “wheel of laughs”, from his point of view it can be said that the farther one gets from the centre, the more the disc “inclines” making it impossible to stay on it. To keep his place on the turntable, he must try to place his centre of gravity on a “vertical” inclined in such a way that the farther he is from the rotation axis, the greater the inclination angle (Figure 1).

However, could it be possible to invent a contraption analogous to an inclined highway for this inertial frame of reference? Of course it is, but the disc would have to be replaced by such a surface that the resultant gravitational force is perpendicular to it at each of its points. The form of such a surface can be computed. It is called a paraboloid. This name isn’t accidental: every vertical cut of a paraboloid is a parabola-the curve along which bodies fall. A paraboloid is obtained by rotating a parabola around its axis.

It is very easy to create such a surface by making a vessel containing water rotate rapidly. The surface of the rotating liquid is precisely a paraboloid. The water particles will stop moving just when the force pressing each particle to the surface is perpendicular to it. To every rotational velocity there corresponds a distinct paraboloid (Figure 2).

It is possible to demonstrate this property by making a solid paraboloid. A small ball placed at any point of a paraboloid rotating with a definite velocity will remain at rest. This means that the force acting on it will be perpendicular to the surface. In other words, a rotating paraboloid behaves as a flat surface. One can walk along such a surface and feel stable, just as on the Earth. However, the direction of the vertical will change during the walk.

Centrifugal phenomena are widely employed in technology. For example, the construction of a centrifuge is based on the use of these phenomena.

A centrifuge is a drum which rotates rapidly around its axis. What will happen if various objects are thrown into such a drum filled to the brim with water?

Let us drop a metal ball into the water—it will go to the bottom but not along our vertical; in moving away from the axis of rotation all the time it will come to a halt at the side. Now let us throw a cork ball into the drum—it, on the contrary, will immediately begin moving towards the axis of rotation and settle there.

If the drum of this model of a centrifuge has a large diameter, we shall notice that the acceleration increases sharply as the ball moves away from the centre.

The phenomena which take place do not puzzle us at all. There is an additional radial force within the centrifuge. If the centrifuge is rotating rapidly enough, its “bottom” is the lateral surface of the drum. The metal ball “sinks” in the water, but the cork ball “floats” The farther a body “falling” in the water is from the axis of rotation, the “heavier” it becomes.

In sufficiently perfected centrifuges, the rotational velocity can be raised to 60,000 rpm, i.e. \(10^{3}\) rps. At a distance of 10 cm from the axis of rotation, the acceleration due to the radial gravitational force will be approximately equal to \[40 \times 10^{6} \times 0.1 = 4 \times 10^6~\mathrm{m/s^2}\] i.e. 400,000 times greater than terrestrial acceleration.

It is clear that the Earth’s gravitation may be neglected for such machines; we really have the right to regard the lateral surface of the drum as the “bottom” in a centrifuge.

The fields of application of a centrifuge become clear from what we have said. If we want to separate the heavy particles in a mixture from the light ones, it is always advisable to apply a centrifuge. Everybody knows the expression: “The muddy liquid has settled.” If dirty water stands long enough, the sediment (usually heavier than the water) will settle to the bottom. However, the process of settling may take months, but with the aid of a good centrifuge it is possible to clean up the water instantly.

Centrifuges rotating with velocities of tens of thousands of revolutions per minute are capable of separating the finest particles of sediment not only from water but also from viscous fluids.

Centrifuges are applied in the chemical industry for separating crystals from the solution out of which they grew, for dehydrating salts and for cleaning varnishes; they are used in the food industry for separating syrup from sugar.

The centrifuges which are applied in separating solid or liquid components from a large number of fluids are called separators. Their main application is the processing of milk. Milk separators whirl with velocities of 2000–6000 rpm; the diameters of their drums are as large as 5 m.

Centrifugal casting is widely applied in metallurgy. Even at velocities of 300–500 rpm the liquid metal flowing into the rotating cast is pressed against its outer surface with a considerable force. Metal pipes cast by this method are denser, more uniform and without blisters or cracks.

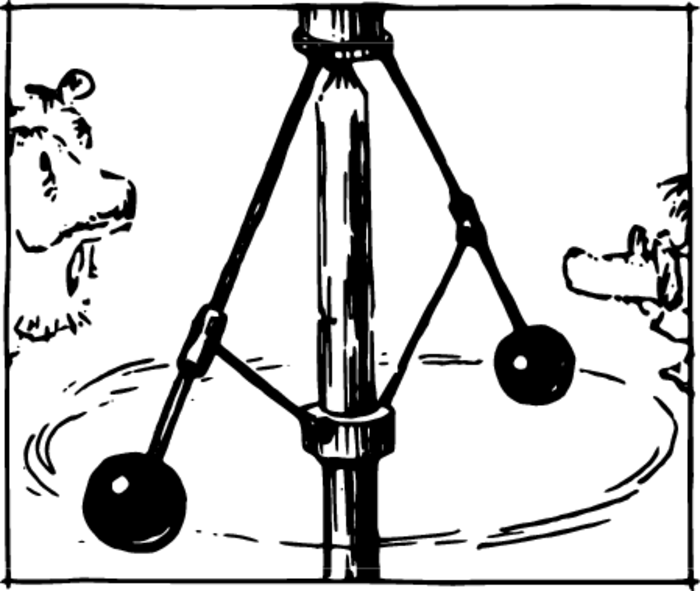
Here is another application of centrifugal force. A simple instrument that serves as a governor of the number of revolutions of the rotating parts of a machine is depicted in Figure 3. This instrument is called a centrifugal governor. As the velocity of rotation increases, the centrifugal force grows, and the small balls of the governor move farther away from its axis. The rods attached to the balls are deflected, and when the deflection reaches a definite level computed by an engineer, some electrical contacts may be broken, and in the case of a steam engine, for example, valves may be opened letting out excess steam. This will decrease the velocity of rotation and return the rods to their normal position.

Here is an interesting experiment. Place a small cardboard disc on the axis of an electric motor. Switch on the electricity and bring a piece of wood in contact with the whirling disc. A fairly thick beam can be sawed in half as easily as by a steel saw.

An attempt to saw wood by means of cardboard can only evince a smile if one employs it as a hand saw. Why then does the rotating cardboard cut wood? The cardboard particles on the boundary of the disc experience an enormous centrifugal force. The lateral forces which might alter the plane of the cardboard are insignificant in comparison with the centrifugal ones. By keeping its plane fixed, the cardboard disc acquires the ability of gnawing into the wood.

The centrifugal force arising as a result of the Earth’s rotation leads to the differences in the weight of a body at various latitudes that we spoke of above.

A body weighs less at the equator than at a pole for two reasons. Bodies lying on the Earth’s surface are at different distances from the Earth’s axis depending on the latitude of their locations. Of course, this distance grows in passing from a pole to the equator. Moreover, a body located at a pole is on the axis of rotation, so the centrifugal acceleration is \[a = 4 \pi^{2}n^{2}R = 0\] (the distance from the axis of rotation \(R = 0\)). At the equator, on the contrary, this acceleration is maximum.

The centrifugal force reduces the gravitational force. Therefore, the pressure exerted by a body on a scale (the weight of the body) is minimum at the equator.

If the Earth had a precisely spherical form, then a kilogram weight carried from a pole to the equator would lose 3.5 g in weight. You can easily find this number if you use the expression \(4\pi^{2}n^{2}Rm\) and substitute \(n = 1\) revolution per day, \(R = 6300~km\), and \(m = 1000~\mathrm{g}\). Only don’t forget to convert the units of measurements to seconds and centimetres.

However, a kilogram weight will actually lose 5.3 g, and not 3.5 g. This is the case because the Earth is an oblate sphere called an ellipsoid in geometry. The distance from a pole to the centre of the Earth is about 1/300 less than a terrestrial radius extended to the equator.

This contraction of the Earth was caused by the very same centrifugal force. In fact, it is exerted on all the particles of the Earth. In remote times, the centrifugal force “moulded” our planet-gave it an oblate form.