In order to characterize the velocities that are not constant, physicists use the concept of acceleration.

The change in velocity during a unit of time is called acceleration. Instead of saying “the velocity of a body changed by a in 1 second”, we say more briefly “the acceleration of a body is equal to \(a\).”

If we denote by \(v_{1}\) the speed of a rectilinear motion at the first instant, and by \(v_{2}\) at the next, the rule for calculating the acceleration \(a\) is expressed by the formula \[a = \frac{v_{2} - v_{1}}{t}\] where \(t\) is the time during which the speed builds up.

Speed is measured in cm/s (or m/s, etc.), time in seconds. Hence, acceleration is measured in cm/s per second. A number of centimetres per second is divided by seconds. Thus, the unit of acceleration will be \(\mathrm{cm/s^2}\) (or \(\mathrm{m/s^2}\), etc.).

Of course, the acceleration can change during the course of a motion. However, we shall not complicate our treatment with this inessential fact. We shall implicitly assume that the velocity changes uniformly during the course of a motion. Such a motion is called uniformly accelerated.

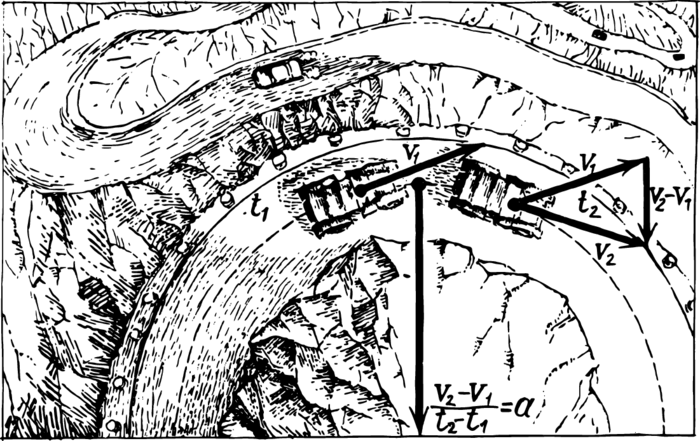
What is acceleration of curvilinear motion?

Since velocity is a vector, a change (difference) in velocity is a vector, and so acceleration is also a vector. In order to find the acceleration vector, one must divide the vector difference between the velocities by the time. But we have already described how to construct a vector change in velocity.

The highway takes a turn. Let us note two nearby positions of a car and represent its velocities by vectors (Figure 1). Subtracting these vectors, we obtain a quantity which is by no means equal to zero; dividing it by the elapsed time, we find the acceleration vector. An acceleration took place even when the speed around the turn did not change. Curvilinear motion is always accelerated. Only uniform rectilinear motion is unaccelerated.

In speaking about the velocity of motion of a body, we always stipulated what our point of view was with regard to the motion. The velocity of a body is relative. From the point of view of one inertial frame of reference it can be great, and from the point of view of another inertial frame of reference it can be small. Don’t we have to make the same kind of stipulations when speaking about acceleration? Of course not. Unlike velocity, acceleration is absolute. From the point of view of all imaginable inertial frames of reference acceleration will be identical. As a matter of fact, acceleration depends on the difference in the velocity of a body between the first and second instants of time, and this difference, as we already know, will be identical from all points of view, i.e. is absolute.

If no force is acting on a body, it can only move without acceleration. Conversely, the action of a force on a body accelerates it; moreover, the greater the force, the greater will be the acceleration. The faster we want to move a loaded waggon, the more we have to strain our muscles. As a rule, two forces act on a moving body: accelerating—the pull, and decelerating—the force of friction or air resistance.

The difference between these two forces, the so-called resultant force, may be directed along or against the motion. In the first case, the body speeds up its motion; in the second case, it slows it down. If these oppositely acting forces are equal to each other, the body will move uniformly, just as though there were no forces acting on it.

But how is a force related to the acceleration it creates? The answer turns out to be very simple. The acceleration is proportional to the force: \[F \propto a\] (The symbol \(\propto\) denotes “is proportional to”.)

Another question still remains to be answered: How do the properties of a body influence its ability to accelerate its motion under the action of one or another force? For it is clear that one and the same force acting on different bodies will give them different accelerations.

We shall find the answer to the question we have posed in the remarkable fact that all bodies fall to the Earth with the same acceleration. This acceleration is denoted by the letter \(g\). In the vicinity of Moscow \(g =981~\mathrm{cm/s^2}\).

Direct observation will not, at first sight, confirm the identity of acceleration for all bodies. The fact is that when a body is falling under ordinary conditions, besides gravity there is another, “hindering” force acting on it – air resistance. Philosophers of antiquity were quite confused by the difference in the way light and heavy bodies fall. A piece of iron falls quickly, but a feather glides through the air. A sheet of paper falls slowly to the ground, but if we roll it up, this same sheet will fall considerably faster. The fact that the atmosphere distorts the “true” picture of the motion of a body under the action of the Earth was already understood by the Ancient Greeks. However, Democritus thought that even if the air were deleted, heavy bodies would always fall faster than light ones. But air resistance can have the opposite effect, for example, a sheet of aluminium foil (all unrolled) will fall more slowly than a small ball made by crumpling a piece of paper.

Incidentally, metallic wire of such a thinness (several microns) is so manufactured now that it glides through the air like a feather.

Aristotle thought that all bodies should fall identically in a vacuum. However, he used this theoretical conclusion to make the following paradoxical deduction: “The falling of different bodies with the same speed is so absurd that the impossibility of the existence of vacuum is clear.”

None of the scientists of antiquity or the Middle Ages guessed that it could be experimentally verified whether bodies fall to the Earth with different or the same accelerations. Only Galileo demonstrated by means of his remarkable experiments (he investigated the motion of balls down an inclined plane and the fall of bodies thrown from the top of the leaning tower of Pisa) that at any given point on the Earth all bodies fall with the same acceleration, regardless of their mass. At the present time such experiments are quite easily performed with the aid of a long tube out of which the air has been pumped. A feather and a stone fall identically in such a tube: only one force acts on the bodies, and that is weight; air resistance has been reduced to zero. In the absence of air resistance, the fall of any body is a uniformly accelerated motion.

Let us now return to the question posed above. How does the ability of a body to accelerate its motion under the action of a given force depend on its properties?

Galileo’s law states that all bodies, regardless of their masses, fall with one and the same acceleration; hence, a mass of \(m \, \mathrm{kg}\) under the action of a force of \(F \,\mathrm{kgf}\) moves with an acceleration \(g\).

Now suppose we are no longer talking about falling bodies, and a force of 1 N is acting on a mass of \(m\) kg. Since acceleration is proportional to force, it will be \(m\) times less than \(g\).

We have arrived at the conclusion that the acceleration a of a body for a given force (1 kgf in our example) is inversely proportional to its mass.

Uniting both conclusions, we may write: \[a \propto \frac{F}{m}\] i.e, for a constant mass the acceleration is directly proportional to the force, and for a constant force inversely proportional to the mass.

This law, relating acceleration to the mass of a body and the force acting on it, was discovered by the great English scientist Sir Isaac Newton (1643–1727), and bears his name.¹

Acceleration is directly proportional to the acting force and inversely proportional to the mass of a body, and does not depend on any other properties of the body. It follows from Newton’s law that it is precisely the mass which is the measure of the “inertness” of a body. For identical forces, it is more difficult to accelerate a body of greater mass. We see that the concept of mass, which we first knew as a “modest” quantity determined by weighing a body on a balance scale, has acquired a new deep meaning: the mass characterizes the dynamic properties of a body.

Newton’s law may be written as follows: \[kF = ma\] where \(k\) is a constant coefficient. This coefficient depends on the chosen units.

Instead of making use of the unit of force (kgf) we already have available, we shall act in a different manner. Just as physicists often try to do, we shall choose our unit of force in such a way that the coefficient of proportionality in Newton’s law becomes equal to unity. Then Newton’s law takes the following form: \[F = ma\] As we have already said, in physics it is customary to measure mass in grams, distance in centimetres, and time in seconds. The system of units based on these three fundamental quantities is called the cgs system.

Let us now choose, using the principle formulated above. the unit of force. A force will then obviously be equal to unity when it imparts the acceleration of 1 cm/s\(^2\) to the mass of 1 g. Such a force received the name dyne in this system.

According to Newton’s law, \(F = ma\), the force will be expressed in dynes if we multiply \(m\) g by \(a \, \mathrm{cm/s^2}\). One therefore makes use of the following notation: \[1~\mathrm{dyne} = 1 \mathrm{g\,cm/s^2}\] The weight of a body is usually denoted by the letter \(W\). The force \(W\) gives the body an acceleration \(g\), and in dynes we obviously have \[W = mg\] But we already had a unit of force—the kilogram-force (N). We immediately find the relation between our new and old units from the last formula: \[1~\mathrm{N} = 981,000~\mathrm{dyn}\] A dyne is a very small force. It is equal to about one milligram of weight.

We have already mentioned the system of units (SI). The name for the new unit of force, newton (N), is fully deserved. For such a choice of units, Newton’s law will look as simple as possible; this new unit is defined as follows: \[1~\mathrm{N} = 1~\mathrm{kg\,m/s^2}\] i.e. 1 N is the force necessary to impart the acceleration of 1 \(\mathrm{m/s^2}\) to the mass of 1 kg.

It is not difficult to relate this new unit to the dyne and the kilogram-force: \[1~\mathrm{N} = 100,000\, \textrm{dyn} =0.102~\mathrm{kgf}\]

Sir Isaac Newton [1643–1717]—a brilliant English physicist and mathematician, one of the greatest scientists in the history of mankind. Newton formulated the basic concepts and laws of mechanics, discovered the law of universal gravitation, creating by the same token a physical picture of the world with remained inviolable until the beginning of the 20th century. He developed a theory of the motion of celestial bodies, explained the most important special features of the Moon’s motion and gave an explanation for the tides. In optics, some remarkable discoveries facilitating the rapid growth of this branch of physics are due to Newton. Newton devised a powerful method of the mathematical investigation of nature; the honour of creating the differential and integral calculus belongs to him. This exerted an enormous influence on the entire subsequent development of physics and facilitated the introduction of mathematical methods of research.