The topic is geological prospecting whose aim is to find deposits of useful minerals under the Earth without digging a pit or sinking a shaft.

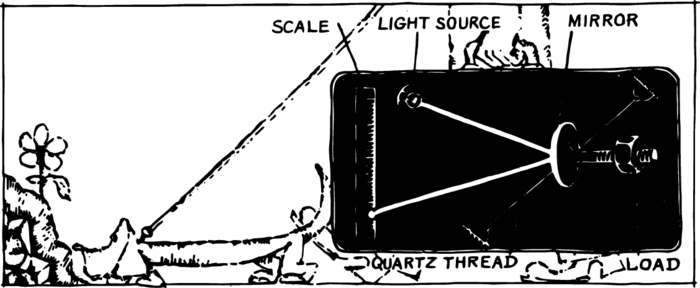
There exist several methods of determining the acceleration of free fall very accurately. It is possible to find \(g\) by simply weighing a standard weight on a spring balance. Geological balances should be extremely sensitive their spring—changes its tension when a load of less than a millionth of a gram is added. Quartz torsion balances yield excellent results. Their construction isn’t complicated in principle. To a horizontally stretched quartz thread a lever is welded whose weight slightly twists the thread Figure 1.

A pendulum is used for the same purposes. Not very long ago pendulum methods of measuring \(g\) were the only ones, and only in the last 10-20 years have the more convenient and precise balance methods begun to supplant them. In any case, measuring the period of oscillation of a pendulum one can find the value of \(g\) accurately enough from the formula \(T = 2 \pi \sqrt{l/g}\).

Measuring values of \(g\) at different places with the same apparatus, we can detect relative changes in the free fall up to one-millionth.

Measuring the value of \(g\) at some place on the Earth’s surface, the experimenter ascertains: here the value is anomalous, it is so much less than the norm or such an amount greater than the norm.

But what is the norm for the value of \(g\)?

There are two natural changes which have long been observed and are well known to researchers in the value of the acceleration of free fallon the Earth’s surface.

First of all, \(g\) decreases from a pole to the equator. This has been spoken of above. Let us only recall that such a change occurs as a result of two causes: firstly, the Earth isn’t a sphere, and a body at a pole will be nearer to the centre of the Earth; secondly, the more a body advances towards the equator, the more will the force of gravity be weakened by the centrifugal force.

The second change in \(g\) is the decrease due to elevation. The greater the distance from the Earth’s centre, the smaller will be the value of \(g\) in accordance with the formula \(g = GM/(R + h)^{2}\), where \(R\) is the radius of the Earth, and \(h\) is the height above sea level.

Therefore, at one and the same latitude and at one and the same height above sea level, the acceleration of free fall should be identical.

Accurate measurements show that deviations from this norm—gravitational anomalies—are found quite often. The cause of an anomaly consists in the heterogeneity of the mass distribution near the place of measurement.

As we explained, the gravitational force due to a large body can be conceptually represented as the sum of forces emanating from the individual particles of the large body. The attraction of a pendulum to the Earth is the result of the action of all the particles of the Earth on it. But it is clear that the nearby particles make the greatest contribution to the resultant force, for the attraction is inversely proportional to the square of the distance.

If heavy masses are concentrated near the place of measurement, \(g\) will be greater than the norm; in the opposite case, \(g\) will be smaller than the norm.

If, for example, we measure \(g\) on a mountain and in an airplane flying over a sea at an altitude equal to the mountain’s height, a greater value will be obtained in the former case. For example, the value of \(g\) is \(0.292\,\mathrm{cm/s^2}\) greater than the norm on Mount Etna in Italy. The value of \(g\) is also higher than the norm on isolated ocean islands. It is clear that in both cases the growth of \(g\) is explained by the concentration of additional masses at the place of measurement.

Not only the value of \(g\) but also the direction of the force of gravity can deviate from the norm. If a load is suspended on a thread, the stretched thread will indicate the vertical for the given place. This vertical may deviate from the norm. A normal vertical can be determined by the stars, since it has been calculated for any geographical point at what place in the sky the vertical to the “ideal” form of the Earth is “set” at a given instant of a day and year.

Imagine that you are performing experiments with a plumb-line at the foot of a large mountain. The load of the plumb-line is attracted by the Earth towards its centre, and by the mountain to one side. Under such conditions, the plumb-line must be deflected from the direction of a normal vertical (Figure 2). Since the Earth’s mass is much greater than that of the mountain, such a deflection will not exceed several seconds of arc. Plumb-line deflections sometimes yield strange results. For example, in Florence the influence of the Appenines leads not to an attraction, but to a repulsion of a plumb-line. The explanation can only be as follows: there are enormous empty spaces in mountains.

Measurements of the acceleration of free fall to the scale of continents and oceans yield remarkable results. Continents are considerably heavier than oceans; therefore, it would seem that the values of \(g\) over continents should: be greater than those over oceans. But in reality, the values of \(g\) measured along a single latitude over oceans and continents are identical, on the average. Again there is only one explanation: continents lie on lighter bedrocks, and oceans on heavier ones. And as a matter of fact, where direct prospecting is possible, geologists ascertain that oceans lie on heavy basaltic bed-rocks, and continents on light granite ones.

But the following question immediately arises: Why do heavy and light bedrocks compensate so exactly for the difference in weight between continents and oceans? Such a compensation cannot be a matter of chance; its cause must be rooted in the construction of the Earth’s shell.

Geologists assume that it is as though the upper layers of the Earth’s shell were floating on an underlying plastic (i.e. easily deformed like wet clay) mass. The pressure at depths of about \(100\,\mathrm{km}\) should be identical everywhere, just as the pressure at the bottom of a vessel filled with water in which pieces of wood of various weights are floating is identical everywhere. Consequently, a column of matter with an area of \(1\,\mathrm{m}^2\) from the surface to a depth of \(100\,\mathrm{km}\) should have the same weight under an ocean and under a continent.

This levelling of pressures (it is called isostasy) is just what leads to the situation where along a single latitude over oceans and continents the values of the acceleration of free fall \(g\) do not differ significantly.

Local gravitational anomalies serve us just as the magic wand, which banged on the ground where there was gold or silver, served little Mook in Hauf’s fairy-tale.

One must look for heavy ore in those places where \(g\) is maximum. On the contrary, light salt deposits are discovered by finding localities with lowered values of \(g\). It is possible to measure \(g\) with an accuracy up to a hundred-thousandth of \(1\,\mathrm{cm/s^2}\).

Prospecting with the aid of pendulums and super-exact scales is called gravitational. It is of great practical value, in particular when looking for oil. The fact is that with gravitational prospecting, it is easy to discover underground salt domes. It so happens that often oil is found at those places too. Moreover, the oil lies at some depth, while the salt is nearer to the Earth’s surface. Oil was discovered in Kazakhstan and in other places by gravitational prospecting.