The first question which Newton asked himself was the following: How does the Moon’s acceleration differ from that of an apple? To put it otherwise, what is the difference between the acceleration \(g\) which the Earth creates on its surface, i.e. at the distance \(r\) from its centre, and the acceleration created by the Earth at the distance \(R\) at which the Moon is located from the Earth?

In order to calculate this acceleration, \(v^{2}/R\), it is necessary to know the speed of the Moon’s motion and its distance from the Earth. Both these figures were known by Newton. The Moon’s acceleration turned out to be approximately equal to \(0.27\,\mathrm{cm/s^2}\). This is about 3600 times less than the value of \(g\), \(980\,\mathrm{cm/s^2}\).

Hence, the acceleration created by the Earth decreases as one recedes from the centre of the Earth. But how rapidly? The distance from the Earth to the Moon equals sixty terrestrial radii. But 3600 is the square of 60. Increasing the distance by a factor of 60, we decrease the acceleration by a factor of \(60^{2}\).

Newton concluded that the acceleration, and therefore also the gravitational force, is inversely proportional to the square of the distance. Further, we already know that the force exerted on a body in a gravitational field is proportional to its mass. Therefore, the first body attracts the second with the force proportional to the mass of the second body; the second body attracts the first with the force proportional to the mass of the first body.

We are dealing with identically equal forces—forces of action and reaction. Consequently, the mutual gravitational force must be proportional to the mass of the first body as well as to that of the second or, to put it otherwise, to the product of the masses.

Thus, \[F = G \, \dfrac{Mm}{r^{2}}\] This is precisely the law of universal gravitation. Newton assumed that this law will be valid for any pair of bodies.

This bold hypothesis is now completely proved. Therefore, the force of attraction between two bodies is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

But what is this \(G\) that entered the formula? This is the coefficient of proportionality. May we assume it to be equal to unity, as we have already repeatedly done? No, we may not: we have agreed to measure mass in grams, distance in centimetres, and force in dynes. The value of \(G\) is equal to the force of attraction between two masses of \(1\,\mathrm{g}\) located at a distance of \(1\,\mathrm{cm}\) from each other. We cannot assume that the force is equal to anything (in particular, to one dyne). The coefficient \(G\) must be measured.

In order to find \(G\), we don’t, of course, have to measure the forces of attraction between gram weights. We are interested in carrying out measurements on massive bodies—the force will be greater then.

If we determine the mass of two bodies, know the distance between them and measure the force of attraction, then \(G\) will be found by a simple calculation.

Such experiments were performed many times. They showed that the value of \(G\) is always one and the same, independent of the material of the attracting bodies and also of the properties of the medium in which they are situated. The quantity G is called the gravitational constant. It is equal to \(6.67\,\mathrm{cm^3\cdot g^{-1}\cdot s^{-2}}\).

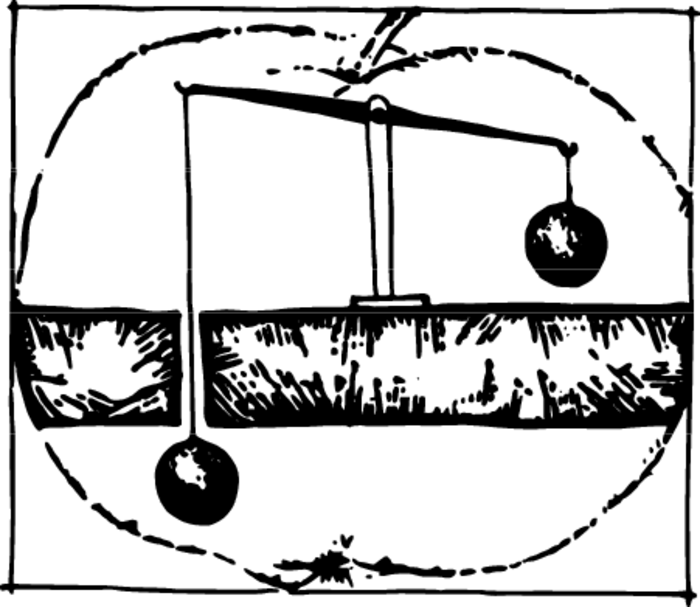
The diagram of one of the experiments on measuring \(G\) is shown in the diagram above Figure 1. Two balls of identical mass are suspended from the ends of a beam of scales. One of them is situated above a lead plate, the other beneath it. By means of its attraction, the lead (100 tons of it are taken for the experiment) increases the weight of the ball on the right and decreases that of the ball on the left. The former outweighs the latter. The value of \(G\) is computed on the basis of the magnitude of the deflection of the beam.

The difficulty in detecting gravitational forces between two objects is explained by the negligible value of \(G\). Two heavy 1000 kg loads pull each other with a negligible force equal in all to only 6.7 dyn, i.e. 0.007 gf, if these objects are situated, say, at a distance of \(1\,\mathrm{m}\) from each other.

But how great are the forces of attraction between celestial bodies? Between the Moon and the Earth \begin{align}  F & = 6.7\times10^{-8} \times \dfrac{6\times 10^{27} \times 0.74 \times 1\times 10^{26}}{(38\times 10^9)^{2}} \\ &= 2\times 10^{25}\,\mathrm{dyn} \\ &\approx 2\times 10^{19}\,\mathrm{kgf} \end{align} and between the Earth and the Sun \begin{align} F & = 6.7\times 10^{-8} \times \dfrac{2\times 10^{33} \times 6 \times 1\times 10^{27}}{(15\times 10^{12})^{2}} \\ &= 3.6\times 10^{27}\,\mathrm{dyn} \\ &\approx 3.6\times 10^{21}\,\mathrm{kgf} \end{align}