We have already witnessed many trips to the Moon. Automatic space probes and manned craft have landed on its surface and then returned. Space probes travelled to Mars and Venus. And soon the other planets will also be visited and automatic stations and people will return from their surface.

We now know the main laws governing interplanetary travel, namely the principle of rocket motion and the method of calculating the different speeds that a body requires to orbit a celestial body and to escape its gravitational pull.

Let us take the trip to the Moon as an example. For this we must aim the rocket at a point on the Moon’s orbit. The Moon must arrive at this point at the same time as the rocket. The rocket may follow various trajectories, even a straight one. But it is essential that it attain the Earth’s escape velocity. We must also bear in mind that different trajectories require different amounts of fuel since fuel consumption depends on acceleration. Another factor is that flight time greatly depends on initial velocity. If this is minimum, the trip will take about five days, but if the velocity is increased by \(0.5\,\mathrm{km/s}\), flight time decreases to 24 hours.

It may seem that to get to the Moon the rocket must only reach the region of the Moon’s attraction with zero velocity. After that it will simply fall onto the Moon. But such reasoning is erroneous, since when the rocket has a zero velocity with respect to the Earth, its velocity with respect to the Moon is the velocity of the Moon on its orbit around the Earth but oppositely directed.

The illustration Figure 1 shows the trajectory of a rocket launched at point \(A\) and the path of the Moon. We can imagine that the region of the Moon’s attraction moves along the same path (in this region the only force that acts on the rocket is the Moon’s gravitational pull). When the rocket enters this region at point \(B\), the Moon is at point \(C\) and has a velocity \(v_{M}\) equal to \(1.02\,\mathrm{km/s}\). If at \(B\) the velocity of the rocket with respect to the Earth were zero, with respect to the Moon it would be \(-v_{M}\). The rocket most certainly will miss the Moon.

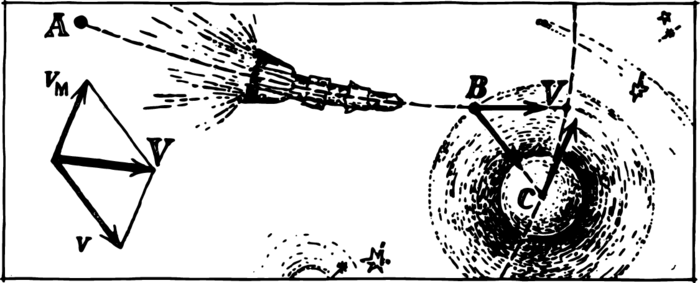
If we are observing the rocket from the Moon, we can be certain that it will meet the Moon at a right angle if its velocity is \(v\). What, then, should its optimal trajectory and velocity be? The rocket must obviously hit point \(B\) not with a zero velocity but with the velocity \(V\) shown in the illustration Figure 1. For this we must simply use the velocity parallelogram shown in the same figure.

We still have some leeway. Velocity vector \(v\) does not have to be pointed at the very centre of the Moon. Besides, the gravitational pull of the Moon broadens the error range.

Calculations show, however, that there is very little elbowroom. The precision in initial velocity must be of the order of several metres per second, and the angle at which the rocket is launched must be set with an accuracy of one-tenth of a degree and the timing of the launching with an accuracy of several seconds.

So the rocket approaches the Moon with a non-zero velocity. Calculations show that this velocity, \(V\), must be \(0.8\,\mathrm{km/s}\). The Moon’s gravitational pull makes the velocity greater and the rocket will collide with the Moon at a velocity of \(2.5\,\mathrm{km/s}\). This is no good of course, since the rocket would disintegrate at impact. The only solution is to lower the speed of descent by using braking rockets. The process of cushioning touchdown requires a large supply of fuel. This formula shows that the rocket will “lose weight” by a factor of 2.7.

If we want the rocket to return to the Earth, it must have some fuel left. The Moon is a relatively small celestial body, only \(3476\,\mathrm{km}\) across and with a mass of \(7.34\times 10^{22}\,\mathrm{kg}\). We can easily see that its orbital velocity (i.e. the velocity required to maintain a satellite in an orbit around it) is \(1680\,\mathrm{m/s}\) and its escape velocity is \(2376\,\mathrm{m/s}\), which means that to leave the Moon, the rocket must have a speed of about \(2.5\,\mathrm{km/s}\). With this minimum initial speed the rocket will return to the Earth after five days and will have the familiar speed of \(11\,\mathrm{km/s}\).

The path of reentry into the Earth’s atmosphere must slope gently, since if there are astronauts inside the rocket the forces of acceleration must be kept to a minimum. But even if we are dealing with an automatic space probe, the probe must make several revolutions around the Earth so that the radius of its elliptical path decreases. Then the reentry vehicle does not get overheated and can safely return to the Earth.

Moon missions cost huge sums of money. If we assume that the return pay-load of a manned flight to the Moon is not less than 5 tons, then the total loaded weight at lift-off must be about 4.5 thousand tons. Experts believe that in the coming 20 years no more astronaut will visit the Moon or, for that matter, any other planet. New propulsion systems with greater exhaust velocities will have to be constructed. However, one cannot be sure of such predictions.