We shall not discuss the sad consequences of the absence of the Moon for poets and lovers. The title of this section should be understood much more prosaically: how the Moon’s presence affects terrestrial mechanics.

In our previous discussion of what forces act on a book lying on a table, we confidently stated: the Earth’s gravity and the reaction force. But, strictly speaking, a book lying on a table is also attracted by the Moon, the Sun and even the stars.

The Moon is our nearest neighbour. Let us forget about the Sun and the stars and consider how much the weight of a body on the Earth will change under the influence of the Moon.

The Earth and the Moon are in relative motion, with respect to the Moon the Earth as a whole (i.e. all points of the Earth) is moving with an acceleration \(Gm/r^{2}\), where \(m\) is the mass of the Moon, and \(r\) is the distance from the centre of the Moon to that of the Earth.

Consider a body lying on the Earth’s surface. We are interested in how much its weight will change owing to the Moon’s action. Terrestrial weight is determined by acceleration with respect to the Earth. In other words, we are therefore interested in how much the acceleration with respect to the Earth of a body lying on the Earth’s surface will be changed by the Moon’s action.

The acceleration of the Earth with respect to the Moon is \(Gm/r^{2}\); the acceleration with respect to the Moon of a body lying on the Earth’s surface is \(Gm/r_{1}^{2}\), where \(r_{1}\) is the distance from the body to the centre of the Moon Figure 1.

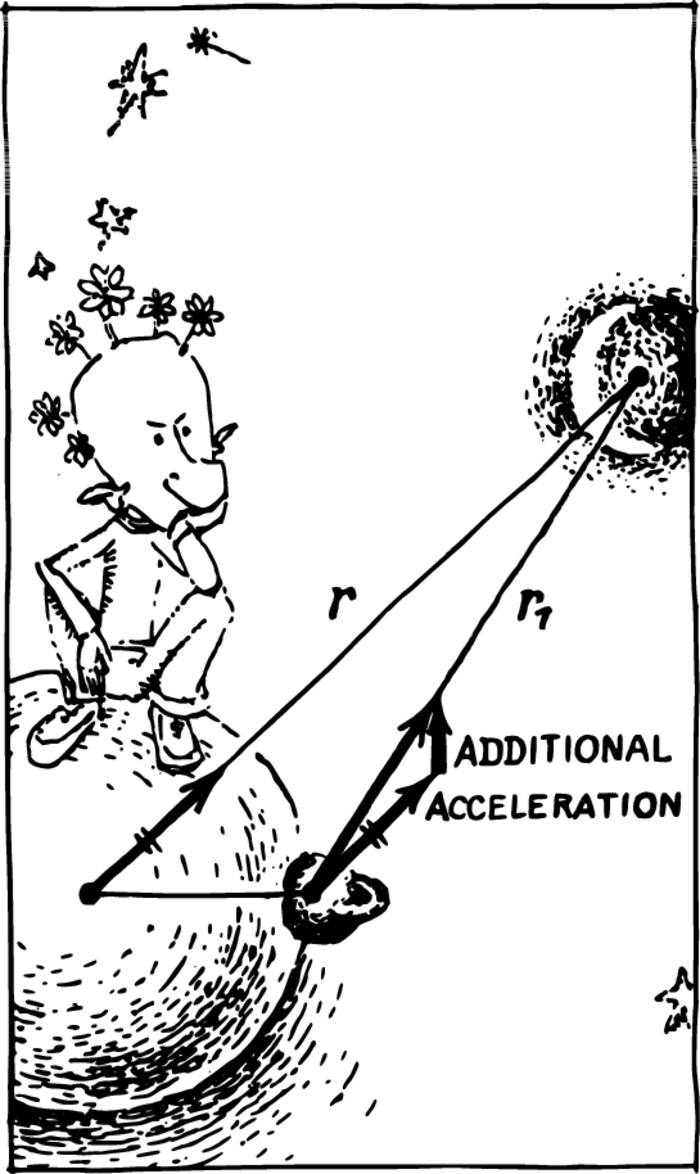
But we should find the additional acceleration of the body with respect to the Earth: it will be equal to the geometrical difference between the appropriate accelerations.

The value of \(Gm/r^{2}\) is a constant number for the Earth, while the value of \(Gm/r_{1}^{2}\) is different at various points on the Earth’s surface. Hence, the geometrical difference of interest to us will differ at various places on the Earth. What will the terrestrial weight be at the place nearest to the Moon, farthest from it and half-way along the Earth’s surface?

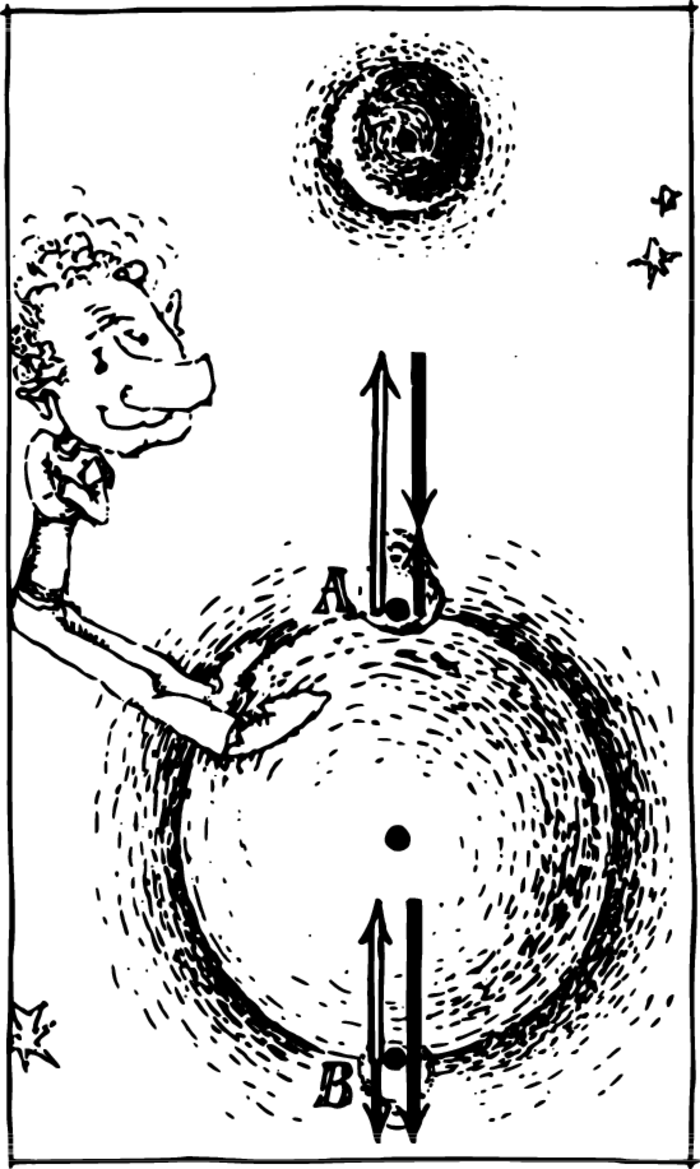
To find the acceleration with respect to the centre of the Earth induced by the Moon on a body, i.e. the correction to the terrestrial gt it is necessary to subtract the constant value of \(Gm/r^{2}\) from the value of \(Gm/r_{1}^{2}\) at the indicated places on the Earth (light arrows in Figure 2).

Moreover, it should be remembered that the acceleration \(Gm/r^{2}\)—the acceleration of the Earth with respect to the Moon—is directed parallel to the line joining their centres. The subtraction of a vector is equivalent to the addition of the inverse vector. The vectors—\(Gm/r^{2}\) are shown by means of bold-face arrows in the figure.

Adding the vectors depicted in the figure, we find what we are interested in: the change in the acceleration of free fall on the Earth’s surface arising as a result of the influence of the Moon.

At the place nearest to the Moon, the resulting additional acceleration will be equal to \[G \, \dfrac{m}{(r - R)^{2}} - G \, \dfrac{m}{r^{2}}\] and directed towards the Moon. Earth’s gravity diminishes; a body at point \(A\) becomes lighter than in the absence of the Moon.

Bearing in mind that \(R\) is much smaller than \(r\) , we are able to simplify the formula written above. Reducing to a common denominator, we obtain: \[\dfrac{GmR \, (2r - R)}{r^{2}(r - R)^{2}}\] Discarding from the parentheses the relatively small magnitude \(R\) subtracted from the much larger magnitudes \(r\) or \(2r\), we obtain \[\dfrac{2GmR}{r^{3}}\] Let us now transfer to the antipode. At point \(B\) the acceleration of a body due to the Moon isn’t greater, but less than the total acceleration of the Earth. But we are now at the farthest side of the Earth from the Moon. A decrease in the Moon’s attraction at this side of the Earth leads to the same result as an increase in the attraction at point \(A\)—to a decrease in the acceleration of free fall. An unexpected result, isn’t it? Here too a body becomes lighter under the action of the Moon. The difference \[G \, \dfrac{m}{(r+ R)^{2}} - G \, \dfrac{m}{r^{2}} \approx - \dfrac{2GmR}{r^{3}}\] turns out to be the same in absolute value as at point \(A\).

Things are different at the median line. Here the accelerations are directed at an angle to each other, and so the subtraction of the total acceleration \(Gm/r^{2}\) of the Earth by the Moon and the acceleration \(Gm/r_{1}^{2}\) of a body lying on the Earth by the Moon must be carried out geometrically Figure 3. We shall depart insignificantly from the median line if we place the body on the Earth in such a way that \(r_{1}\) and \(r\) are equal in magnitude. The vector difference between the accelerations is the base of an isosceles triangle. From the similarity of the triangles depicted in the diagram Figure 3, it is obvious that the required acceleration is as many times less than \(Gm/r^{2}\) as \(R\) is less than \(r\). Consequently, the required addition to \(g\) at the median line on the Earth’s surface equals \[\dfrac{GmR}{r^{3}}\] in magnitude this is one-half of the weakening of the Earth’s force of attraction at the extreme points. As for the direction of this additional acceleration, it again practically coincides, as can be seen from the figure, with the vertical at the given point on the Earth’s surface. It is directed downwards, i.e. leads to an increase in weight.

Thus, the influence of the Moon on terrestrial mechanics consists in a change in weight of bodies located on the Earth’s surface. Moreover, weight diminishes at the nearest and farthest points from the Moon, but grows on the median line, this change in weight in the latter case being half as great as in the former.

Of course, the reasoning carried out is valid for any planet, for the Sun or for a star.

It is not difficult to calculate that neither planets nor stars give even an insignificant fraction of the lunar acceleration.

It is very easy to compare the action of any celestial body with that of the Moon: we must divide the additional acceleration due to this body by the lunar acceleration:

\[\dfrac{GmR}{r^{3}} : \dfrac{Gm_{M}R}{r_{M}^{3}} = \dfrac{m}{m_{M}} \dfrac{r^{3}_{M}}{r^{3}}\] This product will fail to be much less than unity only for the Sun. The Sun is much farther from us than the Moon, but the mass of the Moon is tens of millions of times less than that of the Sun.

Substituting numerical values, We find that under the influence of the Moon terrestrial weight is changed 2.17 times as much as under that of the Sun.

Let us now estimate by how much the weight of terrestrial bodies would be changed if the Moon were to leave its orbit around the Earth. Substituting numerical values in the expression \(2GmR/r^{3}\), we find that the lunar acceleration is of the order of magnitude of \(0.0001\,\mathrm{cm/s^2}\), i.e. of one-ten-millionth of \(g\).

Almost nothing, it would seem. Was it worthwhile to follow with strained attention the solution to a rather complicated mechanical problem for the sake of such an insignificant effect? Don’t hurry with such a conclusion. This “insignificant” effect is the cause of powerful tidal waves. It creates \(1\times 10^{15}\,\mathrm{J}\) of kinetic energy daily, moving enormous masses of water. This energy equals that borne by all the Earth’s rivers.

In fact, the percentage wise change in the quantity we computed is very small. A body which becomes lighter by such an “insignificant” amount will move a bit farther away from the centre of the Earth. But the radius of the Earth is \(6000000\,\mathrm{m}\), and an insignificant deviation will be measured in tens of centimetres.

Imagine that the Moon stopped its motion relative to the Earth and is shining somewhere over an ocean. Calculations show that the water level at this place would rise by \(54\,\mathrm{cm}\). Such a jump in the water level would also occur at the antipode. On the median line between these extreme points, the water level in the ocean would drop by \(27\,\mathrm{cm}\).

Thanks to the Earth’s rotation about its axis, the “places” of rises and falls in the ocean are moving all the time. These are tides. During about six hours, a rise in the water level takes place and the water moves up the shore—this is high tide. Then low tide sets in; it also lasts six hours. Two high tides and two low tides occur every lunar day. The picture of tidal phenomena is greatly complicated by the friction of water particles, the form of the sea bottom and the contour of the shores. For example, tides are impossible in the Caspian Sea simply because the entire surface of the sea is subject to the same conditions.

Tides are also absent from internal seas connected to an ocean by long and narrow straits, for example, the Black and Baltic seas.

Especially big tides occur in narrow bays, where a tidal wave coming in from the ocean rises steeply. For example, in the Gizhiginskaya Inlet on the Sea of Okhotsk, the height of waves attains several metres.

If the ocean shore is sufficiently flat (for example, in France), the rise of water during high tide can change the location of the boundary between land and sea by many kilometres.

Tidal phenomena hinder the Earth’s rotation, for the motion of tidal waves is related to friction. Work must be expended to overcome this friction—it is called tidal. Therefore, the rotational energy, and with it the Earth’s rotational speed about its axis, falls.

This phenomenon leads to the lengthening of the day, as discussed previously.

Tidal friction enables us to understand why one and the same side of the Moon always faces the Earth. At one time, the Moon was probably in a liquid state. The rotation of this liquid sphere about the Earth was accompanied by strong tidal friction, which gradually slowed down the motion of the Moon. Finally, the Moon stopped rotating with respect to the Earth, the tides ceased and the Moon hid half of its surface from our sight.