The question as to how planets move can be answered briefly: obeying the law of gravitation. For the forces of gravitation are the only forces applied to planets.
Since the mass of the planets is much less than that of the Sun, the forces of interaction between the planets do not play a large role. Each of the planets moves almost the way the gravitational force of the Sun alone dictates, as though the other planets did not even exist.
The laws of planetary motion around the Sun follow from the law of universal gravitation.
Incidentally, this isn’t the way things developed historically. The laws of planetary motion were discovered by the outstanding German astronomer Johannes Kepler (1571–1630), before Newton and without the aid of the law of gravitation, on the basis of an almost twenty-year processing of astronomical observations.
The paths or, as astronomers say, the orbits which planets describe around the Sun are very close to circles.
How is the period of revolution of a planet related to the radius of its orbit?
The gravitational force exerted on a planet by the Sun is equal to \[F = \dfrac{G M m}{r^{2}}\] where \(M\) is the mass of the Sun, \(m\) is the mass of the planet, and \(r\) is the distance between them.
But \(F/m\) is, according to the basic law of mechanics, none other than the acceleration; moreover it is centripetal: \[\dfrac{F}{m} = \dfrac{v^{2}}{r}\] The speed of the planet can be represented as the length \(2 \pi r\) of the circumference divided by the period of revolution \(T\). Substituting \(v = 2 \pi r/T\) and the value of the force \(F\) in the acceleration formula, we obtain: \[\dfrac{4 \pi^{2} r}{T^{2}} = \dfrac{GM}{r^{2}} \quad \textrm{i.e.} \quad T^{2}= \dfrac{4 \pi^{2}}{GM} r^{3}\] The coefficient of proportionality preceding \(r^{3}\) is the quantity depending only on the mass of the Sun; it is identical for any planet. Consequently, the following relation holds for two planets: \[\dfrac{T_{1}^{2} }{T_{2}^{2}} = \dfrac{r_{1}^{3} }{r_{2}^{3}}\] The ratio of the squares of the periods of revolution of planets turns out to be equal to the ratio of the cubes of their orbital radii. This interesting law was derived empirically by Kepler. The law of universal gravitation explained Kepler’s observations.
A circular motion of one celestial body around another is only one of the possibilities.
The trajectories of one body revolving around another due to gravitational forces can be very different. However, as shown by calculations and as Kepler had observed before any calculations were made, they all belong to one and the same class of curves, called ellipses.
If we tie a thread to two pins stuck in a sheet of drawing paper, stretch the thread with the point of a pencil and move the pencil in such a way that the thread remains stretched, a closed curve will eventually be drawn on the paper—this is an ellipse (Figure 1). The points where the pins are stuck will be the foci of the ellipse.

Ellipses can have various forms. If the thread is taken much longer than the distance between the pins, then the ellipse will be very similar to a circle. If, on the contrary, the length of the thread barely exceeds the distance between the pins, then an elongated ellipse – almost a stick—will be obtained.
A planet describes an ellipse at one of whose foci is the Sun.
But what kind of ellipses do planets describe? It turns out that they are very close to circles.
The path of the planet nearest to the Sun—Mercury – differs most from a circle. But even in this case, the longest diameter of the ellipse is only 2% greater than the shortest one. The situation is different with the orbits of artificial satellites. Take a look at Figure 2.
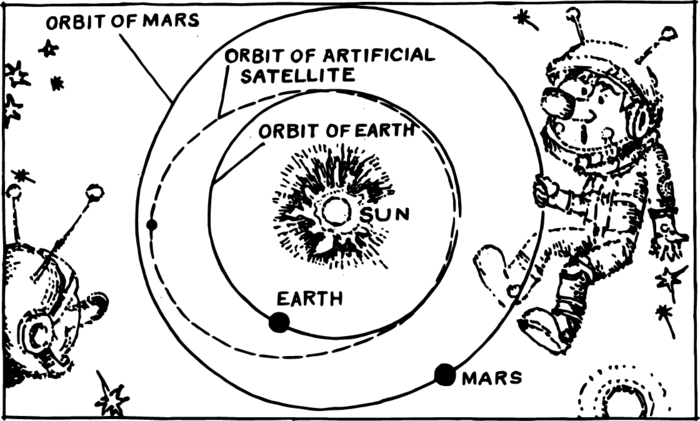
You can’t distinguish the orbit of Mars from a circle. However, since the Sun is located at one of the foci of the ellipse and not at its centre, the distance of a planet from the Sun changes more noticeably. Let us draw a line through the two foci of an ellipse. This line intersects the ellipse at two places. The point nearest to the Sun is called the perihelion, the farthest from the Sun the aphelion. Mercury, when located at the perihelion, is 1.5 times closer to the Sun than at the aphelion.
The major planets describe ellipses around the Sun which are close to circles. However, there are celestial bodies which move around the Sun in greatly flattened ellipses. Among them are comets. Their orbits are not at all comparable with respect to elongation to those of the planets. With regard to the celestial bodies moving in ellipses it can be said that they belong to the solar family. However, casual newcomers also drop in at our system.
There have been observed comets describing curves around the Sun whose forms suggest the following conclusion: the comet will not return; it does not belong to the family of the solar system. The “open” curves described by comets are called hyperbolas.
Such comets move especially fast when passing near the Sun. This is understandable, since the total energy of a comet is constant and, when approaching the Sun, it has the minimum potential energy. Hence, its kinetic energy is maximum at this time. Of course, such an effect takes place for all the planets and for our Earth. However, this effect is slight, since the difference in the potential energies at the aphelion and perihelion is small.
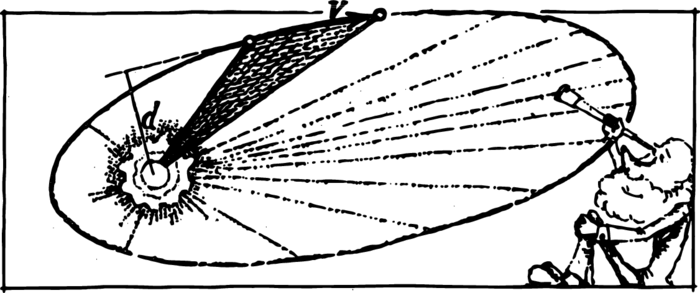
An interesting law of planetary motion follows from the law of conservation of angular momentum.
Two positions of a planet are depicted in Figure 3. From the Sun, i.e. from a focus of the ellipse, the two radii are drawn to the two positions of the planet, and the sector so formed is shaded. We are to determine the area swept out by a radius in a unit of time. For a small angle, the sector swept out by a radius in a second may be replaced by a triangle. The base of the triangle is the speed \(v\) (the distance covered in a second), while the altitude of the triangle is equal to the lever arm \(d\) of the velocity. Therefore, the area of the triangle is \(vd/2\).
The constancy of the quantity \(mvd\) during the motion follows from the law of conservation of angular momentum. But if \(mvd\) is constant, so is the area of the triangle \(vd/2\). We can draw sectors for any interval of time—they will turn out identical in area. The speed of a planet changes, but the so-called areal velocity remains constant.
Not all stars are surrounded by planetary systems. There are quite a few double stars in the sky. Two enormous celestial bodies revolve around each other.
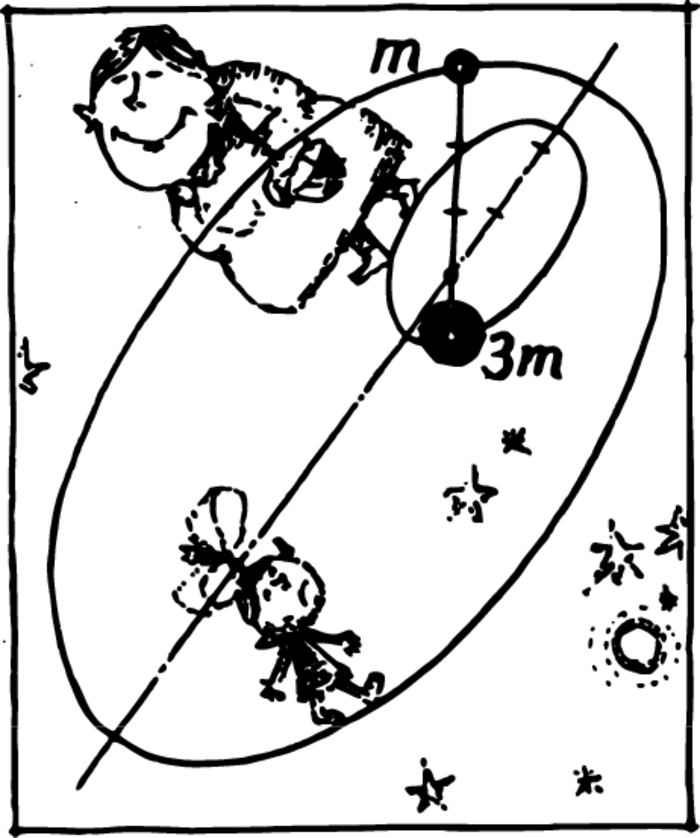
The Sun’s enormous mass makes it the centre of the family. In double stars, both celestial bodies have masses of the same order of magnitude. In this case, we may not assume that one of the two stars is stationary. But how does the motion proceed in this case? We know that each closed system has one stationary (or uniformly moving) point—its centre of mass. Both the stars revolve around this point. Moreover, they describe similar ellipses, which follows from the condition written in Section: Centre of Mass, \(m_{1}/m_{2} = r_{2}/r_{1}\). The ellipse for one star is as many times greater than that for the other as the mass of one star is less than that of the other Figure 4. In the case of equal masses, both the stars will describe identical trajectories around the centre of mass.
The planets of the solar system are in ideal conditions: they are not subject to friction.
The small, artificial celestial bodies created by people—satellites—are not in such an ideal position: frictional forces, however insignificant they may be at first, but none the less perceptible, interfere decisively in their motion.
The total energy of a planet remains constant. The total energy of a satellite falls slightly with every revolution. At first sight, it would seem that friction will slow down the motion of a—satellite. In reality, the opposite occurs.
First of all, recall that the speed of a satellite is equal to \(\sqrt{gR}\) or \(\sqrt{GM/R}\), where \(R\) is its distance from the centre of the Earth, and \(M\) its mass. The total energy of a satellite is equal to \[E = - \, G \, \dfrac{M m}{R} + \dfrac{mv^{2}}{2}\] Substituting the value of the speed of the satellite, we find the expression \(GMm/2R\) for the kinetic energy. We find that the magnitude of the kinetic energy is half as great as that of the potential one, while the total energy is equal to \[E = -\dfrac{G}{2} + \dfrac{Mm}{R}\] In the presence of friction, the total energy falls, i.e. (since it is negative) its magnitude grows; the distance \(R\) starts decreasing: the satellite descends. What happens to the energy summands in this connection? The potential energy decreases (grows in its magnitude), the kinetic energy increases.
Nevertheless, the net change is negative, since the potential energy decreases twice as fast as the kinetic energy increases. Friction leads to a growth in the speed of a satellite and not to a reduction.
It is now clear why a large launch vehicle outflies a small satellite. The friction acting on a large rocket is greater.