The product of the mass of a body by its velocity is called the momentum of the body (another name for it is linear momentum). Since velocity is a vector, momentum Is also a vector quantity. Of course, the direction of the momentum coincides with that of the velocity of motion of the body.

With the aid of our new concept, Newton’s law, \(F = ma\), can be expressed differently. Since \(a =(v_{2} - v_{1})/t\), we have \(F =(mv_{2} - mv_{1})/t\), or \[Ft = mv_{2} - mv_{1}\] The product of the force by the duration of its action is equal to the change in the momentum of the body.

Let us return to recoil.

The result of our investigation of the recoil of a gun can now be formulated more concisely: the sum of the momenta of the gun and the shell will remain equal to zero after the firing. It is obvious that this was also the case before the firing, when the gun and the shell were in a state of rest.

The velocities occurring in the equation \(m_{1}\mathbf{v_{1}} + m_{2}\mathbf{v_{2}} = 0\) are the velocities immediately after the firing. During the subsequent motion of the shell and the gun, the force of gravity and air resistance will begin acting on them, and the Earth will exert an additional frictional force on the gun. But if the shot were fired in a vacuum from a gun hanging in the void, the motion with the velocities \(\mathbf{v_{1}}\) and \(\mathbf{v_{2}}\) would continue arbitrarily long. The gun would move in one direction, and the shell in the opposite direction.

Guns mounted on a platform and firing while in motion are widely applied in current artillery practice. How should the equation we derived be changed in order that it be applicable to a shot fired from such a gun? We may write: \[m_{1}\mathbf{u_{1}} + m_{2}\mathbf{u_{2}} = 0\] where \(\mathbf{u_{1}}\) and \(\mathbf{u_{2}}\) are the velocities of the shell and the gun relative to the moving platform. If the velocity of the platform is \(\mathbf{V}\), then the velocities of the shell and the gun relative to an observer who is at rest will be \[\mathbf{v_{1}} = \mathbf{u_{1}} + \mathbf{V}\] and \[\mathbf{v_{2}} = \mathbf{u_{2}} + \mathbf{V}\] Substituting for \(\mathbf{u_{1}}\) and \(\mathbf{u_{2}}\) in our previous equation, we obtain: \[(m_{1} + m_{2}) \, \mathbf{V} = m_{1}\mathbf{v_{1}} + m_{2}\mathbf{v_{2}}\] In the right-hand side of the equation we have the sum of the momenta of the shell and the gun after the firing. And in the left-hand side? Before the firing, the gun and the shell with a total mass of \(m_{1}+ m_{2}\) move together with the velocity \(\mathbf{V}\). Therefore, in the left-hand side of the equation there is also the total momentum of the shell and the gun, but before the firing.

We have proved a very important law of nature, which is called the law of conservation of momentum. We proved it for two bodies, but it can easily be proved that the same result also holds for any number of bodies. What is the content of this law? The law of conservation of momentum asserts that the sum of the momenta of a number of interacting bodies does not change as a result of this interaction.

It is clear that the law of conservation of momentum will only be valid when no outside forces are exerted on the group of bodies under consideration. Such a group of bodies is called closed in physics.

A rifle and a bullet behave like a closed group of two bodies during a shooting in spite of the fact that they are subject to the Earth’s gravitation. The weight of the bullet is small in comparison with the force exerted by gunpowder gases, and recoil occurs in accordance with one and the same laws, regardless of where the shot will be fired—on the Earth or in a rocket flying through interplanetary space.

The law of conservation of momentum allows us to easily solve various problems dealing with colliding bodies. Let us try to strike one clay ball with another—they will stick together and continue the motion together; if we shoot from a rifle at a wooden ball, it will roll together with the bullet stuck in it; a standing cart will roll if a person takes a running jump into it. All the examples we have given are very similar from the point of view of physics. The rule relating the velocities of the bodies involved in such kinds of collisions can be immediately obtained from the law of conservation of momentum.

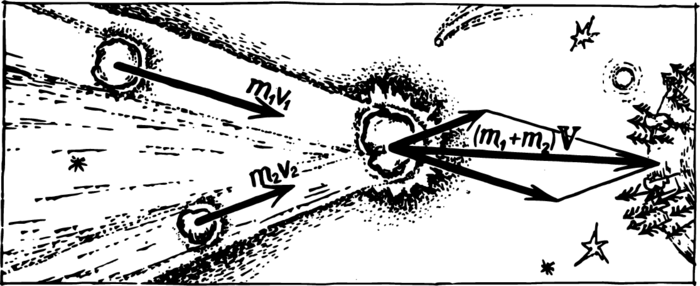
The momenta of the bodies prior to their collision were \(m_{1}\mathbf{v_{1}}\) and \(m_{2}\mathbf{v_{2}}\) they united after the collision, and their total mass is equal to \(m_{1} + m_{2}\). Denoting the velocity of the united body by \(\mathbf{V}\), we obtain: \[m_{1}\mathbf{v_{1}} + m_{2}\mathbf{v_{2}} = (m_{1} + m_{2})\, \mathbf{V}\] or \[\mathbf{V} = \frac{m_{1}\mathbf{v_{1}} + m_{2}\mathbf{v_{2}}}{m_{1} + m_{2}}\] Let us recall the vector nature of the law of conservation of momentum. The momenta \(m\mathbf{v}\) in the numerator of the formula must be added like vectors.

The “uniting hit” when bodies moving at an angle to each other meet is shown in Figure 1. In order to find the speed, we must divide the length of a diagonal of the parallelogram formed by the momentum vectors of the colliding bodies by the sum of their masses.