Even those who have not been at war know that when a gun is fired it jumps back abruptly. When a rifle is fired, recoil in the shoulder occurs. But it is possible to become acquainted with recoil without having recourse to firearms. Pour some water into a test tube, cork it up and suspend it horizontally on two threads (Figure 1). Now turn on a burner under the test tube, the water will begin boiling, and in a couple of minutes the cork will fly out in one direction, while the test tube will be deflected in the opposite direction.

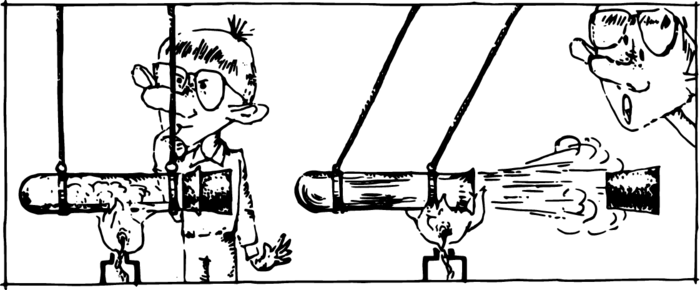
The force which drove the cork out of the test tube is steam pressure. And the force deflecting the test tube is also steam pressure. Both motions arose under the action of one and the same force. The same thing also happens in shooting, only there the action is not that of steam but of gunpowder gas.

Recoil is an inevitable consequence of the principle of equality between an action and its reaction. If the steam acts on the cork, the cork also acts on the steam in the opposite direction, and the steam transmits this reaction to the test tube.

Perhaps the following objection occurs to you: Can one and the same force really lead to such dissimilar effects? The rifle moves backwards only slightly, but the bullet flies far away. We hope, however, that such an objection had not occurred to the reader. Identical forces certainly can lead to different effects: for the acceleration which a body receives (and this is precisely the effect of the action of the force) is inversely proportional to its mass. We must write out the acceleration of one of the bodies (shell, bullet, cork) in the form \(a_{1} = F/m_{1}\); the acceleration of the body experiencing recoil (gun, rifle, test tube) is then \(a_{2} = F/m_{2}\) Since the force is one and the same, we arrive at an important conclusion: the accelerations imparted by the interaction of two bodies participating in a “shot” will be inversely proportional to their masses: \[\frac{a_{1}}{a_{2}} = \frac{m_{2}}{m_{1}}\] This means that the acceleration imparted to the gun when it recoils will be as many times less than the acceleration of the shell as the gun weighs more than the shell.

The acceleration of the bullet, and also of the rifle during recoil, lasts as long as the bullet is moving through the muzzle. Let us denote this time by \(t\). When this time has elapsed, the accelerated motion will become uniform.

For the sake of simplicity, we shall assume the acceleration to be constant. Then the speed with which the bullet flies out of the muzzle of the rifle is \(v_{1} = a_{1}t\), and the speed of recoil is \(v_{2}= a_{2}t\). Since the time during which the accelerations act is one and the same, then \(v_{1}/v_{2} = a_{1}/a_{2}\), and so \[\frac{v_{1}}{v_{2}} = \frac{m_{2}}{m_{1}}\] The speeds with which the bodies fly apart after the interaction will be inversely proportional to their masses.

If we recall the vector nature of velocity, we can rewrite the last relation as follows: \[m_{1}\mathbf{v_{1}} = - m_{2}\mathbf{v_{2}}\] the minus sign indicates that the velocities \(\mathbf{v_{1}}\) and \(\mathbf{v_{2}}\) are oppositely directed.

Finally, let us rewrite our equation once again bringing the products of mass by velocity to one side: \[m_{1}\mathbf{v_{1}} + m_{2}\mathbf{v_{2}} = 0\]