We shall roll a small cart down two very smooth inclined planes. Let us take two boards, one much shorter than the other, and place them on one and the same support. Then one inclined plane will be steep, and the other will be gently sloping. The tops of both boards—the starting places of the cart—will be at the same height. In which case do you suppose will the cart acquire the greater speed by rolling down its inclined plane? Many people will decide that it will be the one which rolls down the steeper board.

An experiment will show that they are wrong—in both cases the cart will acquire the same speed. While a body is moving along an inclined plane, it is subject to the action of a constant force? namely (Figure 1), the component of gravity directed along the line of its motion. The speed \(v\) which a body acquires moving with acceleration a along a path of length \(s\) is equal, as we know, to \(\sqrt{2as}\).

What makes it evident that this magnitude does not depend on the angle of inclination of the plane? We see two triangles in Figure 1. One of them depicts the inclined plane. The small leg of this triangle denoted by \(h\) is the height from which the motion begins; the hypotenuse \(s\) is the path through which the body passes in its accelerated motion. The small force triangle with leg \(ma\) and hypotenuse \(mg\) is similar to the large one, since they are right triangles, and their angles as angles with mutually perpendicular sides are equal. Hence, the ratio of the legs should be equal to that of the hypotenuses, i.e, \[\frac{h}{ma} = \frac{s}{mg} \,\, \textrm{or} \,\, as = gh\] We have proved that the product \(as\), and hence the final speed of a body rolling down an inclined plane, is independent of the angle of inclination but depends only on the height from which the downward motion began. The speed \(v = \sqrt{2gh}\) for all inclined planes subject to the sole condition that the motion began from one and the same height \(h\). This speed turned out to be equal to the speed of free fall from height \(h\).

Let us measure the speed of a body at two places on the inclined plane—at heights \(h_{1}\) and \(h_{2}\). Denote the speed of the body when it passes through the first point by \(v_{1}\) and its speed when it passes through the second point by \(v_{2}\).

If the initial height from which the motion began is \(h\), the square of the speed of the body at the first point will be \(v_{1}^{2} = 2g (h - h_{1})\) and at the second point \(v_{2}^{2}= 2g (h - h_{2})\). Subtracting the former from the latter, we shall find out how the speeds of the body at the initial and end points of an arbitrary piece of an inclined plane are related to the heights of these points: \[v_{2}^{2} - v_{1}^{2} = 2g (h_{1} - h_{2})\] The difference between the squares of the speeds depends only on the difference in height. Note that the equation we have obtained is equally suitable for upward motion and downward motion. If the first height is less than the second (ascent), the second speed is less than the first.

This formula can be rewritten in the following way: \[v_{2}^{2} - v_{1}^{2} = 2g (h_{1} - h_{2})\] We wish to emphasize by means of this formulation that the sum of half the square of the speed and g times the height is identical for all the points on the inclined plane. One may say that the quantity \((v^{2}/2) + gh\) is conserved during the motion.

What is most remarkable in the law we have found is that it is valid for frictionless motion on any hill and, in general, along any path consisting of alternating ascents and descents of various slopes. This follows from the fact that any path can be broken up into rectilinear portions. The smaller we take the segments, the closer will the broken line approximate the curve. Each straight line segment into which the curvilinear path has been broken up may be regarded as part of an inclined plane, and the rule we have found may be applied to it.

Therefore, the sum \((v^{2}/2) + gh\) is identical for all the points of the trajectory. Consequently, a change in the square of the speed does not depend on the form or length of the path along which a body moved but is determined solely by the difference in height of the initial and end points of the motion.

It may seem to the reader that our conclusion does not coincide with his daily experience: on a long, gently sloping path a body does not gather any speed at all, and eventually comes to a halt. This is the way things are, but we haven’t taken the force of friction into account in our reasoning. The above formula is valid for motion within the Earth’s gravitational field under the action of only the single force of gravity. If the frictional force is small, the derived law will be satisfied rather well. A sled with metal runners slides down smooth icy mountains with very little friction. It is possible to build long icy paths that begin with a steep descent on which a great speed is gathered and then twist up and down fantastically. The end of a trip on such a hill (when the sled stops by itself) would occur at a height equal to that of the start, provided that friction were entirely absent. But since it is impossible to avoid friction, the point at which the motion of the sled started will be higher than the place where it stops.

The law which asserts that the final speed pf a motion subject to the force of gravity is independent of the form of the path can be applied to the solution of various interesting problems.

“Looping-the-loop” in a vertical circle has been frequently presented at circuses as an exciting stunt. A cyclist or a cart with an acrobat in it is placed on a high platform. He then accelerates while descending. Now he is ascending. Look, he is in an upside-down position. then again a descent, and the loop has been looped. Let us consider a problem which a circus engineer must solve. At what height should the platform from which the descent begins be made, so that the acrobat might loop-the-loop within falling? We know a necessary condition: the centrifugal force pressing the acrobat against the cart must balance the oppositely directed gravitational force.

Hence \(mg \leqslant mv^{2}/r\), where \(r\) is the radius of the loop, and \(v\) is the speed of the motion at the top of the loop. In order that this speed be attained, it is necessary to begin the motion from a place which is a certain quantity \(h\) higher than the top of the loop. Since the initial speed of the acrobat is equal to zero, we have \(v^{2} = 2gh\) at the top of the loop. But, on the other hand, \(v^{2} \geqslant gr\). Hence, between the height \(h\) and the radius of the loop there is the relation \(h \geqslant r/2\). The platform must be raised by at least half the radius of the loop above the top of the loop. Taking into account the inevitable frictional force, we shall, of course, have to choose our height with a margin of safety.

And here is another problem. Let us take a large, very smooth dome so that friction is minimum. Let us place a small object at the top and give it the opportunity of sliding down the dome by means of hardly noticeable push. Sooner or later the sliding body will get detached from the dome and start falling. We can easily answer the question as to just when the body breaks away from the surface of the dome: at the moment of the break the centrifugal force must equal the radial component of the weight (at this instant the body will cease pressing the dome, and this is precisely the moment of the break). Two similar triangles can be seen in Figure 2; the moment of the break is depicted. Let us form the ratio of a leg to the hypotenuse for the force triangle and set it equal to the corresponding ratio for the other triangle: \[\frac{mv^{2}/r}{mg} = \frac{r-h}{r}\]

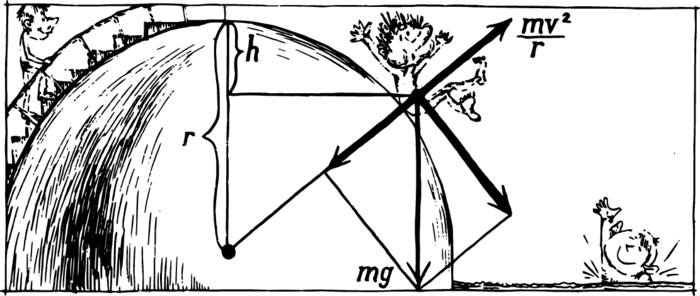
Here \(r\) is the radius of the spherical dome, and \(h\) is the difference in height between the start and finish of the sliding. Let us now make use of the independence of the final speed of the form of the path. Since the initial speed of a body is assumed equal to zero, we have \(v^{2} = 2gh\). Substituting this value in the above proportion and performing arithmetical transformations, we find \(h = r/3\). Hence, the body will break away from the dome at a height which is one-third of a radius lower than the top of the dome.