Momentum is conserved in every collision between two bodies. As for energy, it will necessarily decrease, as we have just explained, because of various kinds of friction.

However, if the colliding bodies are made of elastic material, say of ivory or steel, the energy loss will be insignificant. Such collisions, for which the sums of the kinetic energies before and after the collision are identical, are called ideally elastic.

A small loss of kinetic energy takes place even in collisions of the most elastic materials; it reaches, for example, 3-4% with ivory billiard balls.

The conservation of kinetic energy in elastic collisions permits us to solve a number of problems.

Consider, for example, a head-on collision between balls of different mass. The momentum equation has the form (we assume that the second ball has been stationary prior to the collision) \[m_{1}v_{1} = m_{1}u_{1} + m_{2}v_{2}\] and the energy equation \[\frac{m_{1}v_{1}^{2}}{2} = \frac{m_{1}u_{1}^{2}}{2} +\frac{m_{2}u_{2}^{2}}{2}\] where \(v_{1}\) is the speed of the first ball before the collision, and \(u_{1}\) and \(u_{2}\) are the speeds of the balls after the collision.

Since the motion takes place along a straight line (the one passing through the centres of the balls-this is just what is meant by a head-on collision), the bold-face type denoting vectors has been replaced by italics. From the first equation we have: \[u_{2} = \frac{m_{1}}{m_{2}} = (v_{1} - u_{1})\] Substituting this expression for \(u_{2}\) in the energy equation, we obtain: \[\frac{m_{1}}{2}(v_{1}^{2} - u_{1}^{2})=\frac{m_{2}}{2} \left[ \frac{m_{1}}{m_{2}}(v_{1} - u_{1}) \right]^{2}\] One of the solutions of this equation is \(v_{1} = u_{1}\) which yields \(u_{2} = 0\). But this answer doesn’t interest us, since the equalities \(v_{1} = u_{1}\) and \(u_{2} = 0\) imply that the balls did not collide at all. We therefore look for another solution of the equation. Dividing by \(m_{1} (v_{1} - u_{1})\) we obtain: \begin{align} \frac{1}{2} (v_{1} + u_{1}) & = \frac{1}{2}\frac{m_{1}}{m_{2}} (v_{1} - u_{1}) \,\, \textrm{i.e.}\\ m_{2}v_{1} + m_{2}u_{1} & = m_{1}v_{1} - m_{1}u_{1} \,\, \textrm{or} \\ (m_{1} - m_{2}) v_{1} &= (m_{1} + m_{2})u_{1} \end{align} which yields the following value for the speed of the first ball after the collision: \[u_{1} = \frac{m_{1}=m_{2}}{m_{1}+m_{2}}v_{1}\] In a head-on collision with a stationary ball, the moving ball rebounds (negative \(u_{1}\)) if its mass is less. If \(m_{1}\) is greater than \(m_{2}\) both the balls continue the motion in the direction of the collision.

In case of an exact head-on collision during a game of billiards, one often observes the following scene: the driving ball comes to a sudden stop, and the target ball heads for a pocket. This is explained by the equation we have just found. The masses of the balls are equal, the equation yields \(u_{1} = 0\), and so \(u_{2} = v_{1}\). The colliding ball halts, and the second ball begins its motion with the former’s previous speed. It is as though the balls have exchanged speeds.

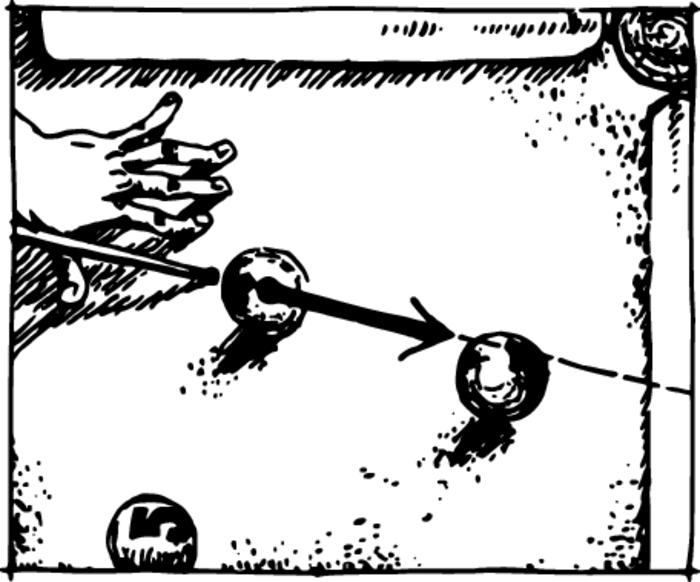
Let us consider another example of a collision between bodies in accordance with the law of elastic collisions, namely an oblique collision between bodies of equal mass (Figure 1). The second body was stationary prior to the collision, so the laws of conservation of momentum and energy have the form: \[m \mathbf{v_{1}} = m\mathbf{u_{1}}+ m\mathbf{u_{1}}\] Cancelling the mass, we obtain: \begin{align}  \mathbf{v_{1}} &= \mathbf{u_{1}}+ \mathbf{u_{2}}\\ v_{1}^{2} &= u_{1}^{2} + u_{2}^{2} \end{align}

Vector \(\mathbf{v_{1}}\) is the vector sum of \(\mathbf{u_{1}}\) and \(\mathbf{u_{2}}\), but this means that the lengths of the velocity vectors form a triangle.

What kind of triangle is this? Recall the Pythagorean theorem. Our second equation is an expression of it. This means that the velocity triangle must be a right triangle with hypotenuse \(\mathbf{v_{1}}\) and legs \(\mathbf{u_{1}}\) and \(\mathbf{u_{2}}\). Hence, \(\mathbf{u_{1}}\) and \(\mathbf{u_{2}}\) form right angles with each other. This interesting result shows that in any oblique elastic collision, bodies of equal mass fly apart at right angles.