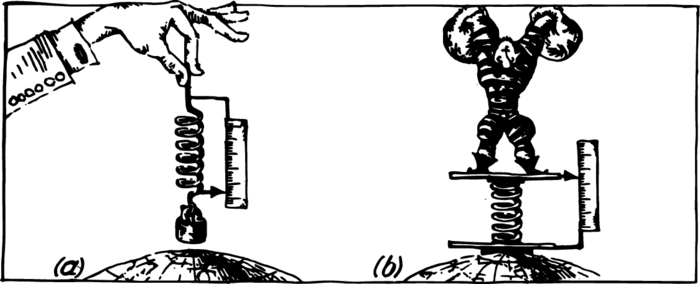
Weight is the force with which a body is attracted by the Earth. This force can be measured with a spring balance. The more the body weighs, the more the spring on which it is suspended will be stretched. With the aid of a weight taken as the unit it is possible to calibrate the spring—make marks which will indicate how much the spring has been stretched by a weight of one, two, three, etc., kilograms. If, after this, a body is suspended on such a scale, we shall be able to find the force (gravity) of its attraction by the Earth, by observing the stretching of the spring (Figure 1 (a)). For measuring weights, one uses not only stretching but also contracting springs (Figure 1 (b)). Using springs of various thickness, one can make scales for measuring very large and also very small weights. Not only coarse commercial scales are constructed on the basis of this principle but also precise instruments used for physical measurements.

A calibrated spring can serve for measuring not only the force of the Earth’s attraction, i.e. weight, but also other forces. Such an instrument is called a dynamometer, which means a measurer of forces. You may have seen how a dynamometer is used for measuring a person’s muscular force. It is also convenient to measure the tractive force of a motor by means of a stretching spring (Figure 2).

The weight of a body is one of its very important properties. However, the weight depends not only on the body itself. As a matter of fact, the Earth attracts it. And what if we were on the Moon? It is obvious that its weight would be different—about six times less, as shown by computations. In fact, even on the Earth, weight is different at various latitudes. At a pole, for example, a body weighs 0.5% more than at the equator.

However, for all its changeability, weight possesses a remarkable peculiarity—the ratio of the weights of two—bodies remains unchanged under any conditions, as experiments have shown. If two different loads stretch a spring identically at a pole, this identity is completely preserved even at the equator.

In measuring weight by comparing it with the weight of a standard, we find a new property of bodies, which is called mass.

The physical meaning of this new concept—mass—is related in the most intimate way to the identity in comparing weights which we have just noted.

Unlike weight, mass is an invariant property of a body depending on nothing except the given body.

A comparison of weights, i.e. measurement of mass, is most conveniently carried out with the aid of ordinary balance scales (Figure 3). We say that the masses of two bodies are equal if the balance scale on whose pans these bodies are placed is in perfect equilibrium. If a load is in equilibrium on a balance scale at the equator, and then the load and the weights are transported to a pole, the load and the weights change their weight identically. Weighing at the pole will therefore yield the same result: the scale will remain balanced.

We can even verify this state of affairs on the Moon. Since the ratio of bodies’ weights will not change there either, a load placed on a scale will be balanced by the same weights there. The mass of a body remains the same no matter where it is.

Units of mass and weight are related to the choice of a standard weight. Just as in the case of the metre and the second, people tried to find a natural standard of mass. The same commission used a definite alloy to make a weight which balanced one cubic decimetre of water at four degrees Centigrade¹. This standard was called the kilogram.

Later, however, it became clear that it isn’t so easy to “take” one cubic decimetre of water. Firstly, the decimetre, as a fraction of the metre, changed along with the refinement of the metre’s standard. Secondly, what kind of water should we take? Chemically pure water? Twice distilled? Without any trace of air? And what should be done about admixtures of “heavy water”? To top off all our misfortunes, accuracy in measuring a volume is noticeably less than that in weighing.

It again became necessary to reject a natural unit and accept a specially made weight as the unit of mass. This weight is also kept in Paris together with the standard for the metre.

One-thousandth and one-millionth of a kilogram—the gram and the milligram—are widely used for measuring mass. The Tenth and Eleventh General Conferences of Weights and Measures developed the International System of Units (SI), which was then ratified by most countries as national standards. The name “kilogram” (kg) is retained by mass in this system. Every force, including of course weight, is measured in newtons (N) in this system. We shall find out a bit later why this unit was given such a name and how it is defined.

The new system will undoubtedly not be immediately and universally applied, and so it is still helpful to recall that the kilogram of mass (kg) and the kilogram of force (kgf) are units of different physical quantities, and it is impossible to perform arithmetical operations on them. Writing \(5~\operatorname{kg} + 2~\operatorname{kgf} = 7\) is just as meaningless as adding metres to seconds.