It is more difficult to overcome a steep rise than a gradual one. It is easier to roll a body up an inclined plane than to lift it vertically. Why is this so, and how much easier is it? The law of the addition of forces permits us to gain an understanding of these matters.

Figure 1 depicts a waggon on wheels which is held on an inclined plane by the tension in a string. Besides pull, two other forces are acting on the waggon—its weight and the force of the reaction of the support which always acts along the normal to a surface, regardless of whether the surface of the support is horizontal or inclined.

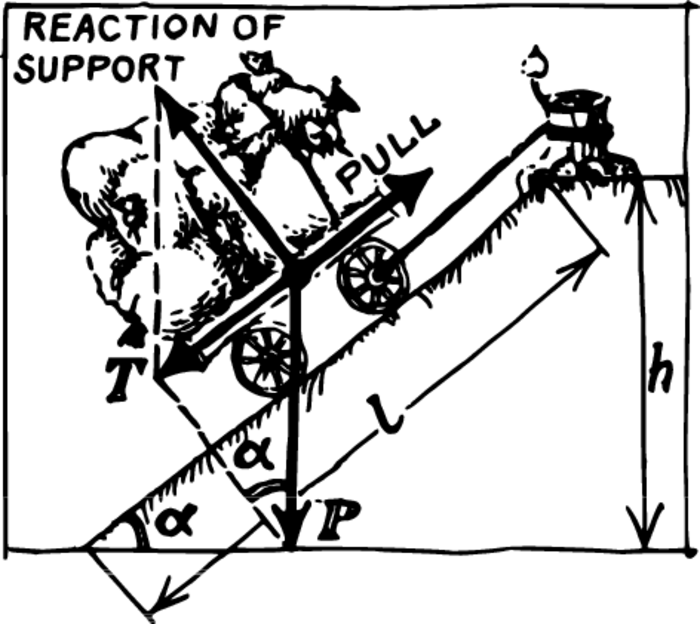
As has already been said, if a body rests on a support, the latter counteracts the pressure Of, as we say, creates the reaction force.

We want to know to what degree it is easier to pull a waggon up along an inclined plane than to lift it vertically.

We decompose the forces in such a way that one component is directed along, and the other perpendicular to, the surface on which the body is moving. In order for the body to be at rest on the inclined plane, the tension in the string must balance only the tangential component. As for the second component, it is balanced by the reaction of the support.

We can find the force we are interested in, i.e. the tension \(T\) in the rope, either by means of a geometrical construction or with the aid of trigonometry. The geometrical construction consists in dropping a perpendicular from the end point of the weight vector \(P\) to the plane.

One can find two similar triangles in the figure. The ratio of the length \(l\) of the inclined plane to its height \(h\) is equal to the ratio of the corresponding sides of the force triangle. Thus, \[\frac{T}{P} = \frac{h}{l}\]

The less the plane is inclined (the smaller the value of \(h/l\)), the easier it will be, of course, to pull the body upwards.

And now, for those who are acquainted with trigonometry: since the angle between the normal component of the weight and the weight vector is equal to the angle of inclination \(\alpha\), of the plane (these are angles with mutually perpendicular sides), we have \[\frac{T}{P} = \sin \alpha \; \mathrm{and} \; T = P \sin \alpha\] Therefore, it is \(1/\sin \alpha\) times easier to wheel a waggon up a plane with the angle of inclination \(\alpha\) than to lift it vertically.

It is helpful to memorize the values of the trigonometric functions for angles of \(30^\circ\), \(45^\circ\) and \(60^\circ\). Knowing these numbers for the sine (\(\sin {30^\circ} = 1/2; \; \sin {45^\circ} = \sqrt{2}/2; \; \sin {60^\circ} = \sqrt{3}/2\), we get a good idea of the amount of force saved by moving up an inclined plane.

It is evident from our formulas that for a \(30^\circ\) angle of inclination, the force we exert will be half the weight of the body: \(T = P/2\). For angles of 45° and 60°, we have to pull the rope with forces equal to about 0.7 and 0.9 of the weight of the waggon. As we see, such steeply inclined planes do not make our task much easier.