If I waited half an hour and then another hour, I would lose one and a half hours of time all told. If I were given a rouble and then two more, I would receive three roubles in all. If I bought 200 g of grapes and then another 400 g, I would have 600 g of grapes. We say that time, mass and other similar quantities are added arithmetically.

However, not every quantity can be added and subtracted so simply. If I say that it is 100 km from Moscow to Kolomna and 40 km from Kolomna to Kashira, it does not follow from this that Kashira is located at a distance of 140 km from Moscow. Distances are not added arithmetically.

How else can quantities be added? We shall easily find the required rule on the basis of our example. Let us draw three points on a piece of paper indicating the relative locations of the three places of interest to us (Figure 1). We can construct a triangle with these three points as vertices. If two of its sides are known, it is possible to find the third. For this, however, we must know the angle between the two given segments.

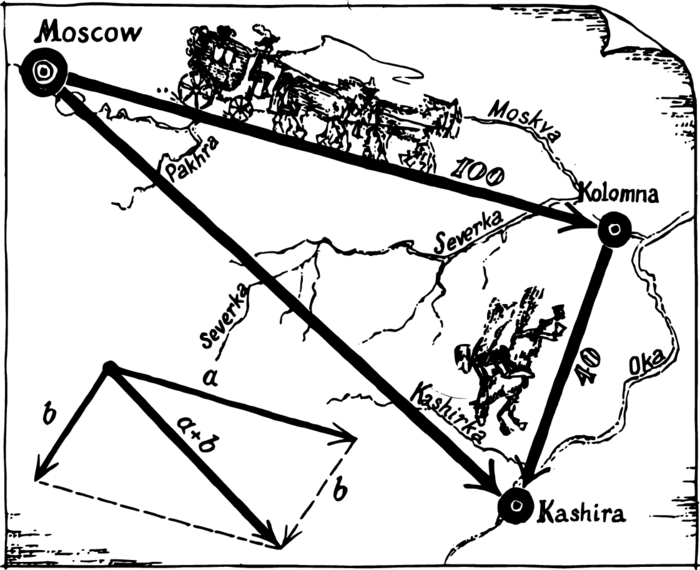
The trip from Moscow to Kolomna can be represented by an arrow whose direction shows where we are moving to. Such arrows are called vectors. So the trip from Kolomna to Kashira is represented by another vector.

Now, how do we show the trip from Moscow to Kashira? With a vector, of course. We will start this vector at the beginning of the first vector and end it at the end of the second. The sought path will be the line that completes the triangle.

The kind of addition just described is called geometrical and the quantities which are added in this manner are called vectors.

In order to distinguish the initial point of a segment from its end point, we add an arrow to it. Such a segment—a vector—indicates a length and a direction.

This rule is also applied in adding several vectors. Passing from the first point to the second, from the second to the third, etc., we cover a path which can be represented by a broken line. But it is possible to go directly from the starting point to the terminal point. This segment closing up the polygon will be precisely the vector sum.

A vector triangle also shows, of course, how to subtract one vector from another. For this we draw them from one point. The vector drawn from the end point of the second vector to the end point of the first will be the vector difference.

Besides the triangle rule, one may make use of the equivalent parallelogram rule (Figure 1). This rule requires that we construct a parallelogram on the vectors we are adding, and draw the diagonal from the point of their intersection. It is clear from the figure that the diagonal of the parallelogram is precisely the segment which closes up the triangle. Hence, both rules are equally suitable.

Vectors are used for describing not only displacements. Vector quantities are frequently found in physics.

Consider, for example, a velocity of motion. Velocity is the displacement during a unit of time. Since the displacement is a vector, the velocity is also a vector, and it has the same direction. In the course of motion along a curve, the direction of displacement is changing all the time. How then can we answer the question about the direction? A small segment of a curve has the same direction as a tangent. Therefore, the displacement and velocity of a body are directed along the tangent to the path of motion at each given instant.

In many cases one must add and subtract velocities according to the rule for vectors. The need to add velocities arises when a body participates simultaneously in two motions. Such cases are not uncommon: a person walks inside a train and, in addition, moves together with the train; a drop of water trickling down the window pane of a train moves downwards under the action of its weight and travels along with the train; the Earth moves around the Sun and together with the Sun moves with respect to the other stars. In all these and other similar cases, velocities are added in accordance with the rule for adding vectors.

If both motions take place along a single line, then vector addition reduces to ordinary addition when both motions have the same direction, and to subtraction when they have opposite directions.

But what if the motions take place at an angle? Then we turn to geometrical addition.

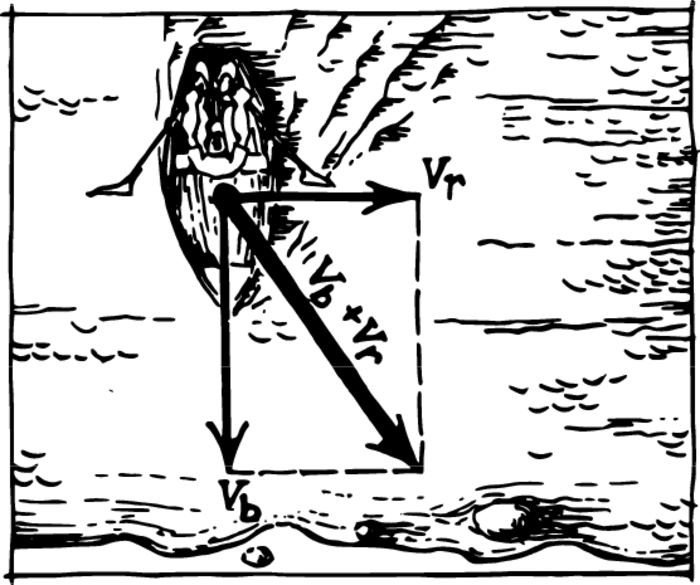
If in crossing a swiftly flowing river you steer perpendicular to the current, you will be carried downstream. The boat participates in two motions: across the river and along the river. The total velocity of the boat is shown in Figure 2.

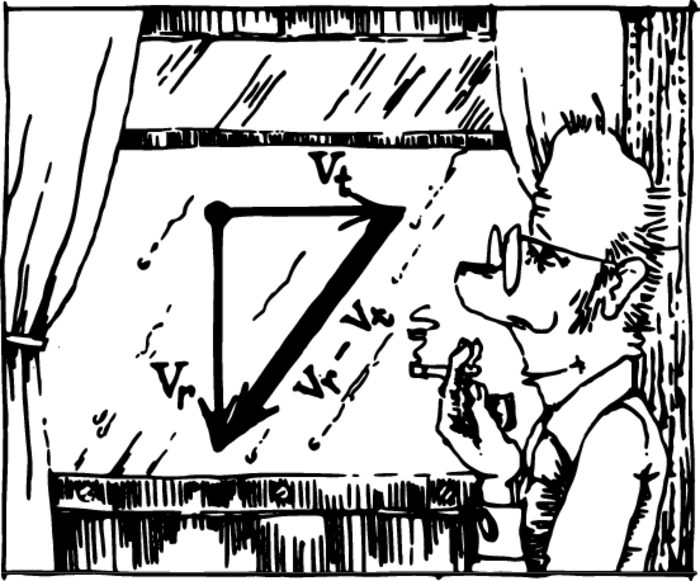
Another example. What does the motion of a stream of raindrops look like from the window of a train? You have no doubt observed rain from train windows. Even in windless weather it moves slantwise, as if a wind blowing towards the train from ahead were deflecting it (Figure 3).

If the weather is windless, a raindrop falls vertically downwards. But during the time the drop is falling near the window, the train has travelled a fair distance leaving the vertical line of fall behind; this is why the rain seems to be slanting.

If the velocity of the train is \(\mathbf{v}_{t}\), and the velocity of the raindrop is \(\mathbf{v}_{r}\), then the velocity of its fall relative to a passenger of the train is obtained by the vector subtraction of \(\mathbf{v}_{t}\) from \(\mathbf{v}_{r}\).¹ The velocity triangle is shown in Figure 3. The direction of the slanting vector indicates the direction of the rain; now it is clear why we see the rain slanting. The length of the slantwise arrow yields the magnitude of this velocity in the chosen scale. The faster the train goes and the slower the raindrop falls, the more the stream of raindrops seems to slant.