Force, just as velocity, is a vector quantity. For it always acts in a definite direction. Therefore, forces should also be added according to the rules which we have just discussed.

We often observe examples in real life which illustrate the vector addition of forces. A rope on which a package is hanging is shown in Figure 1. A person is pulling the package to one side with a string. The rope is being stretched by the action of two forces: the force of the weight of the package and the force that the person exerts on it.

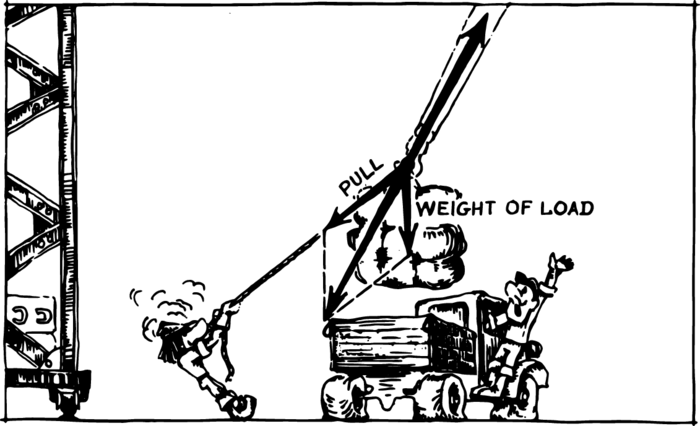
The rule of vector addition of forces allows us to determine the direction of the rope and compute the tension. The package is at rest; hence, the sum of the forces acting on it must be equal to zero. And we can also put it this way—the tension in the rope must be equal to the sum of the weight of the package and the force pulling it to one side with the aid of the string. The sum of these forces yields the diagonal of a parallelogram which will be directed along the rope (for otherwise it could not be “annihilated” by the tension in the rope). The length of this arrow will represent the tension. The two forces acting on the package could be replaced by such a force. The vector sum of forces is therefore sometimes called the resultant.

There very often arises a problem which is inverse to the addition of forces. A lamp is suspended on two ropes. In order to determine the tension in the ropes, we must decompose the weight of the lamp along these two directions.

From the end point of the resultant vector (Figure 2) we draw lines parallel to the ropes up to the points of intersection. The parallelogram of forces is constructed. Measuring the lengths of the sides of the parallelogram, we find (in the same scale in which the weight is represented) the magnitude of the tension in the rope.

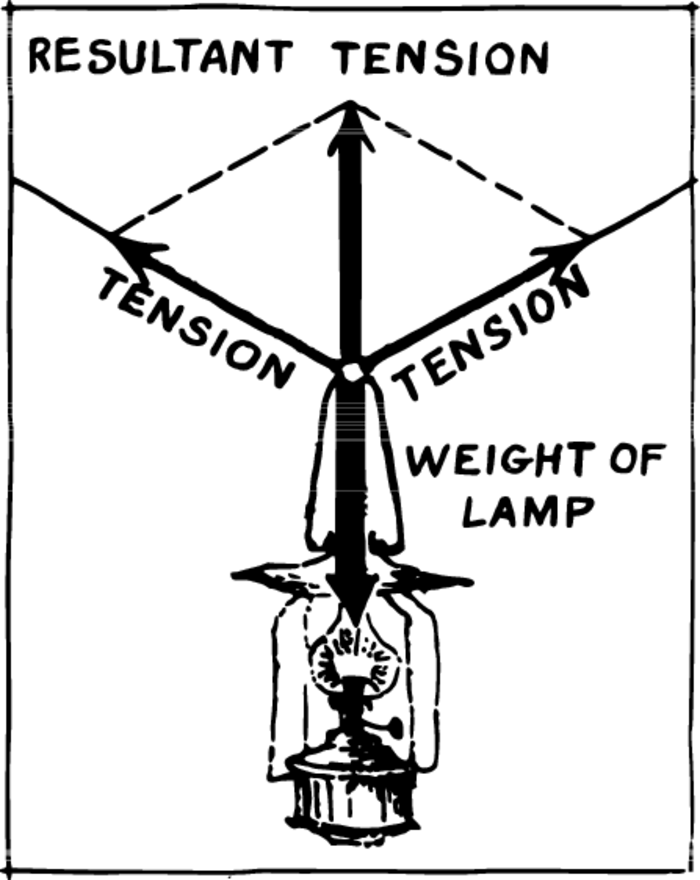
Such a construction is called a decomposition of force. Every number can be represented in an infinite number of ways as the sum of two or several numbers; the same thing can also be done with a force vector: any force can be decomposed into two forces—sides of a parallelogram—one of which can always be chosen arbitrarily. It is also clear that to each vector there can be attached an arbitrary polygon.

It is often convenient to decompose a force into two mutually perpendicular forces—one along a direction of interest to us and the other perpendicular to this direction. They are called the tangential and normal (perpendicular) components of force.

The component of force in a particular direction, constructed by a decomposition along the sides of a rectangle, is also called the projection of the force in this direction.

It is clear that in Figure 3 \[F^{2} = F_{t}^{2} + F_{n}^{2}\] where \(F_{t}\) and \(F_{n}\) are the projections of the force in the chosen direction and normal to it.

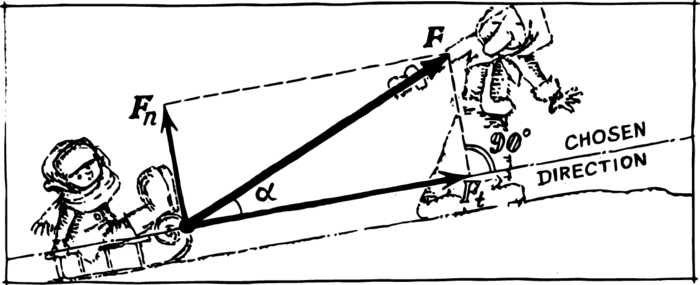
Those who know some trigonometry will establish without difficulty that \[F_{t} = F \cos \alpha\] where \(\alpha\) is the angle between the force vector and the direction onto which it is projected.

A very curious example of the decomposition of forces is given by the motion of a sailboat. How does it manage to sail against the wind? If you ever watched a sailboat doing this, you might have noticed that it zigzagged. Sailors call such a motion tacking.

Of course, it is impossible to sail directly against the wind, but why is it possible to sail against the wind at all, if only at an angle?

The possibility of beating against the wind is based on two circumstances. The wind always pushes the sail at right angles to the latter’s plane. Look at Figure 4 (a): the force of wind is decomposed into two components—one of them \(F_{\textrm{slip}}\) makes the air slip past the sail and, hence, does not act on the sail, and the other—the normal component-exerts pressure on the sail.

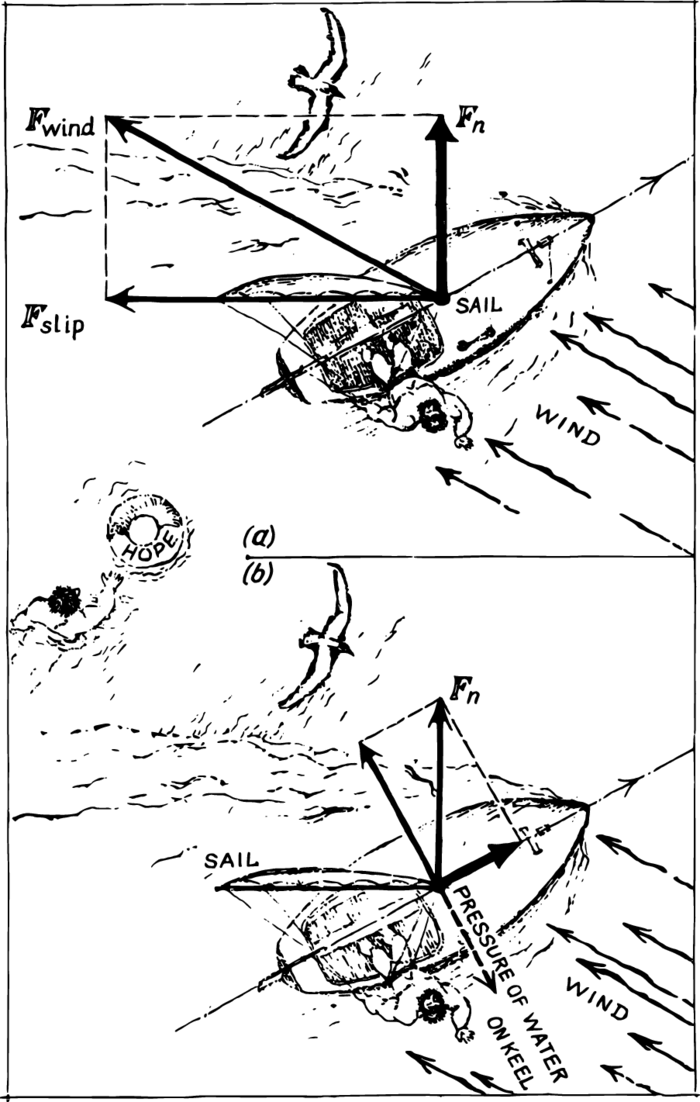
But why does the boat move not in the direction of the wind but roughly in the direction of the bow? This is explained by the fact that a movement of a boat across its keel line would meet with a very strong resistance on the part of the water. Therefore, in order for a boat to move forward, it is necessary that the force pressing on the sail should have a forward component along the keel line. This aspect is illustrated in Figure 4 (b).

In order to find the force which drives the boat forward, we must decompose the force of the wind a second time. We have to decompose the normal component along and across the keel line. It is just the tangential component that drives the boat at an angle towards the wind, and the normal component is balanced by the pressure of the water exerted on the keel. The sail is set in such a way that its plane bisects the angle between the direction of the path of the boat and that of the wind.